哈密顿力学
哈密顿力学比拉格朗日力学更具对称性,其中一方面体现在自变量的量纲上:
[q_\alpha\dot{q_\alpha}]=[q_\alpha^2/t][p_\alpha q_\alpha]=[Lt]显然哈密顿力学的自变量量纲和广义坐标的选取无关,这在接下来的讨论中会体现得更明显。
狄拉克通过对哈密顿力学的量子化,建立起了二者的桥梁,这在 波函数和薛定谔方程 中提到:
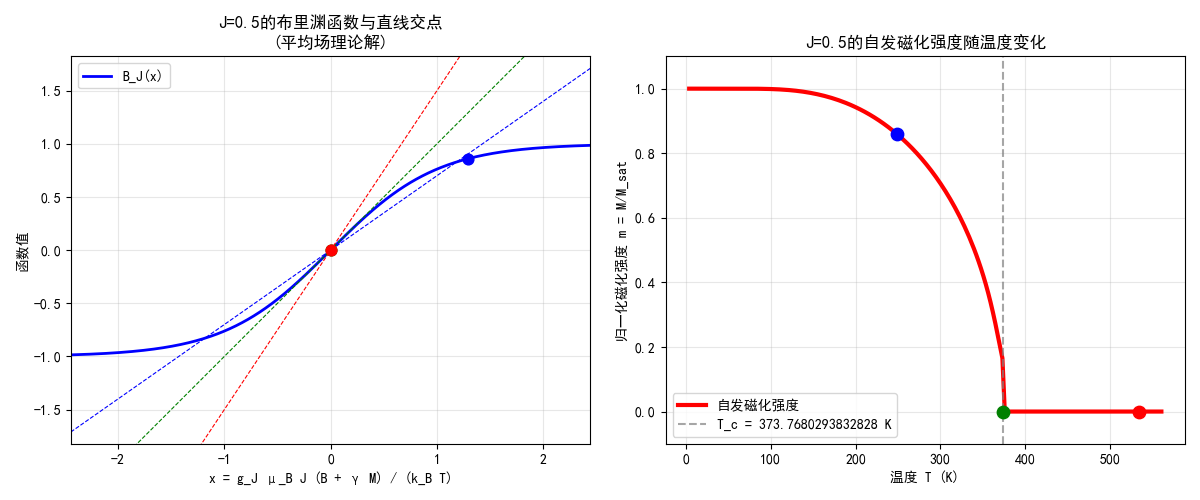
\{P_i,X_j\}=\delta_{ij},[P_i,X_j]=i\hbar\delta_{ij}哈密顿正则方程拉格朗日动力学方程为:
\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_\alpha}-\frac{\partial L}{\partial q_\alpha}= 0,(\alpha=1,2,\cdots,s)是s个二阶常微分方程。它同时可以改写为2s个一阶微分方程:
\begin{cases}
\dot{p}_\alpha=\dfrac{\partial L}{\partial q_\alpha}\quad (\alpha=1,2,\cdots,s)\\\\
p_ ...
拉格朗日动力学
拉格朗日方程拉格朗日关系将真实坐标用广义坐标表示:
\vec{r}_i = \vec{r}_i(q_1, q_2, \cdots, q_{N-k}, t)\dot{\vec{r}}_i = \sum_{\alpha=1}^{N-k}\frac{\partial \vec{r}_i}{\partial q_\alpha}\dot{q}_\alpha + \frac{\partial \vec{r}_i}{\partial t}分别对$\dot{q}_\beta$和$q_\beta$求导:
\begin{aligned}
\frac{\partial \dot{\vec{r}}_i}{\partial \dot{q}_\beta} &= \frac{\partial}{\partial \dot{q}_\beta}\left(\sum_{\alpha=1}^{N-k}\frac{\partial \vec{r}_i}{\partial q_\alpha}\dot{q}_\alpha + \frac{\partial \vec{r}_i}{\partial t}\right)\\
&= \f ...
达朗贝尔原理
约束取一个简单的例子,两个二维质点由一个刚性的轻杆链接,求解质点的运动可以有两种方法:
考虑杆的弹力(约束力),列出牛顿方程;
考虑杆的几何约束,不考虑弹力。
如果使用第一种方法,需要假设弹性力的作用,则4个运动方程中出现新的未知量弹性力,需要额外的约束方程来求解;如果使用第二种方法,则可以通过设置三个广义坐标——质心的坐标和杆的角度来描述系统的运动,进而列出拉格朗日方程。
这两种方法对应牛顿力学和拉格朗日力学,也是对约束的不同处理方法。根据约束的存在与否和性质,可以将力学问题做如下分类:
\begin{cases}
\text{无约束} & \text{自由系统} \\
\text{有约束} & \text{非自由系统}
\end{cases}\begin{cases}
\text{约束的不等式性} &
\begin{cases}
\text{等式} & \text{双面约束} \\
\text{不等式} & \text{单面约束}
\end{cases} \\
\text{约束是否含时} &
\begin{cases}
\text{不含时} & \text{定常约束} \\ ...
级数与留数定理
级数展开与留数定理在上一节中,我们谈论到如果能将函数级数展开,那么可以根据负次幂级数来计算围线积分。以下是洛朗定理:
洛朗定理:设 $f(z)$ 在 $D$ 内解析,$D$ 是包含点 $z_0$ 的圆盘,且 $f(z)$ 在 $z_0$ 处有孤立奇点,则存在一个收敛于 $z_0$ 的圆盘 $D’$,使得在 $D’$ 内,$f(z)$ 可以展开为:
f(z) = \sum_{n=-\infty}^{+\infty} a_n (z - z_0)^n其中:
a_n = \frac{1}{2\pi i} \oint_C \frac{f(z)}{(z - z_0)^{n+1}} dz取$n=-1$,我们可以得到:
\oint_C f(z) dz=2\pi i a_{-1}复数$a_{-1}$被称为留数,它是函数在孤立奇点处的一个重要性质,通常记为$a_{-1}=\underset{z=z_0}{\text{Res}} f(z)$,这样求围线积分就可以写为:
\oint_C f(z) dz=2\pi i \underset{z=z_0}{\text{Res}} f(z)如果围道内存在多个孤立 ...
随机过程
随机过程随机过程是指在时间和空间上变化的随机变量的集合,记为:
\{X(t), t \in T\}其中,$X(t)$是随机变量,$t$是时间或空间的参数,$T$是参数的取值范围。一般称$t$为事件,$X(t)$为随机过程的状态。一次实验观测到的函数$x(t)$称为随机过程的样本函数或轨迹。
随机过程可以用来描述随时间变化的随机现象,如股票价格、气温、人口等。根据随机变量的性质,可以分为以下几类:
离散时间随机过程:参数$t$取离散值,如整数或有限集合。
连续时间随机过程:参数$t$取连续值,如实数或区间。
离散状态随机过程:随机变量$X(t)$取离散值,如整数或有限集合。
连续状态随机过程:随机变量$X(t)$取连续值,如实数或区间。
一些常见的随机过程可以分类如下表格:
随机过程类型
时间
状态
一维随机游走
离散
离散
马尔可夫链
离散
离散
泊松过程
连续
离散
布朗运动
连续
连续
自回归过程
离散
连续
随机过程的数字特征随机过程的数字特征是指随机过程的统计特性,主要包括以下几个方面:
均值:随机过程的均值是指随机变量$X(t)$ ...
随机变量及其分布
概率论基础随机试验满足以下三个条件的实验称为随机试验:
试验的结果不确定,不能事先预知。
可以在相同的条件下重复进行。
试验的结果属于一个确定的集合,这个集合称为样本空间,记作 $S$。样本空间中的每一个元素称为样本点,记作 $\omega$。样本空间中所有可能的结果构成了试验的结果集。
样本空间$S$的子集称为事件,记作$A$。事件可以是单个样本点,也可以是多个样本点的集合。其中,$S$也是样本空间的子集,称为必然事件;空集$\emptyset$也是样本空间的子集,称为不可能事件。
事件的关系如下:
并事件:若事件A和事件B至少有一个发生,则记该事件为$A \cup B$,称为事件A或事件B发生。
积事件:若事件A和事件B同时发生,则记该事件为$A \cap B$,称为事件A且事件B发生。
互不相容事件:若事件A和事件B互不相容,则记该事件为$A \cap B = \emptyset$,称为事件A和事件B不相容。
包含事件:若事件A发生必导致事件B发生,则称事件B包含事件A,记作$A \subseteq B$。
相等事件:若$A \subseteq B,B \subseteq ...
复变函数
复数复数是实数的扩展,形式为 $z = x + iy$,其中 $x$ 和 $y$ 是实数,$i$ 是虚数单位,满足 $i^2 = -1$。复数可以在平面上表示为点 $(x, y)$,也可以用极坐标表示为 $z = re^{i\theta}$,其中 $r = |z| = \sqrt{x^2 + y^2}$ 是模,$\theta = \arg(z)$ 是幅角。
复数的运算定义用坐标形式表示为:
加法:$z_1 + z_2 = (x_1 + x_2) + i(y_1 + y_2)$
乘法:$z_1 z_2 = (x_1 x_2 - y_1 y_2) + i(x_1 y_2 + y_1 x_2)$
复共轭:$\overline{z} = x - iy$
模:$|z| = \sqrt{x^2 + y^2}$
用极坐标表示时,复数的乘法和除法可以简化为:
乘法:$z_1 z_2 = r_1 r_2 e^{i(\theta_1 + \theta_2)}$
除法:$z_1 / z_2 = \frac{r_1}{r_2} e^{i(\theta_1 - \theta_2)}$
复共轭:$\over ...
波动光学(偏振)
偏振光学
偏振态
马吕斯定律
自然光
部分偏振光
圆偏振光
椭圆偏振光
偏振度
双折射率晶体
晶体的双折射现象
介电常数张量
确定折射的方向
双折射晶体的应用
偏振器
相位延迟片(波晶片)
偏振光学偏振态一般将光的偏振态分为五种:
线偏振光:$\vec{E(t)}=\vec{A}\cos{(\omega t)}$,光矢量的模随时间变化,而方向不变,可以分解为两个正交的线偏振光分量:E_x=A_x\cos{(\omega t)},E_y=\pm A_y\cos{(\omega t)}
自然光:自然光是大量不同且独立的线偏振光的几何,因而具有轴对称性;
部分偏振光:自然光经过反射或折射,部分方向的线偏振光减弱,从而对称性减小;
圆偏振光:$\vec{E(t)}=\vec{A}\cos{(\omega t+\phi)}$,光矢量的模不变,方向随时间变化,可以分解为两个正交的线偏振光分量:E_x=A_x\cos{(\omega t)},E_y=\pm A_y\sin{(\omega t)}依据正负号分别表示右旋圆偏振光和左旋圆偏振光;
椭圆偏振光:分解为两个非正交的线偏振 ...
偏微分方程的分离变量法2
偏微分方程的分离变量法1 谈到了正交多项式和场论基础。为了求解偏微分方程,可以在相应坐标系下使用场论结果表示相应算子,使用分离变量法使其转化为多个独立的常微分方程问题,然后使用正交多项式展开。
直角坐标系波动方程以一般的一维波动方程为例:
\begin{cases}
\frac{\partial^2 u}{\partial t^2}=c^2\frac{\partial^2 u}{\partial x^2}+f(x,t)&\text{波动方程}\\
a_1u(x=0,t)+a_2u_x(x=0,t)=g(t)&\text{边值条件1}\\
b_1u(x=0,t)+b_2u_x(x=0,t)=h(t)&\text{边值条件2}\\
u(x,t=0)=\varphi(x),u_t(x,t=0)=\psi(x)&\text{初始条件}
\end{cases}该问题可以拆分为两个问题:
齐次方程的非齐次边界问题:$u_1(x,t)$
非齐次方程的齐次边界问题:$u_2(x,t)$
$u_1(x,t)$和$u_2(x,t)$的解都需要用到齐次方程的正交多项式展开,然后分别根据边界条件和外力项决 ...
偏微分方程
偏微分方程
重要的数学物理方程
波动方程
热传导方程
Laplace方程和Poisson方程
Schrödinger方程
偏微分方程常微分方程是指未知函数仅与一个自变量有关的微分方程:
F(x,y,y',y'',\cdots,y^{(n)})=0而偏微分方程是指未知函数与多个自变量有关的微分方程:
F[x_i,\frac{\partial y}{\partial x_i},\frac{\partial^2 y}{\partial x_i\partial x_j},\cdots(i,j=0,1,\cdots,n)]=0偏微分方程有线性和非线性之分,这里以二阶微分方程为例:
\begin{cases}
\text{线性} &
\begin{cases}
\text{齐次} &
\sum_{i,j=1}^{n}a_{ij}\dfrac{\partial^2 y}{\partial x_i\partial x_j}+\sum_{i=1}^{n}b_{i}\dfrac{\partial y}{\partial x_i}+cy=0\\
\text{非齐次} &
\sum_{i,j=1}^{ ...