小径

Where is the particle? EPR佯谬 Bell不等式 Where is the particle?对量子力学中的粒子到底处于何处，长久以来有以下多种看法： Realist Position：现实主义学派认为粒子有一个确定的位置，而测量给出了这个位置的结果。这说明量子力学并不是一个完备的学说，因为他没有办法精确地给出粒子的真实位置，而只是给出了在该位置的几率。 Orthodox Position：正统学派认为，粒子哪里也不在，是测量使得波函数坍缩。 Agnonstic Position：要讨论粒子测量前在哪里，首先就需要测量。不可知学派认为讨论“测量前”的状态是没有意义的。 EPR佯谬一个$\pi$介子会衰变为一个正电子和负电子： \pi^0\Rightarrow e^++e^-当我测量其中一个粒子的自旋时，我可以立即知道另一个粒子的自旋——这是因为$\pi$介子的自旋是0。 对于现实主义学派，这是没有问题的，发射的粒子的自旋已经被确定好。但是对于正统学派却不然——如果两个粒子相距足够远，那么“从该粒子自旋确定另一粒子的自旋”的信息的传递就就会超过光速，这也成 ...

单元系的单相平衡条件（热动平衡判据） 单元复相系的热力学基本方程 单元系的复相平衡条件 复相平衡的性质 相变平衡曲线 超临界点和等温线 相变的分类 临界现象和朗道连续相变理论 单元系的单相平衡条件（热动平衡判据）热力学第二定律指出，孤立系统的熵朝着增加的方向进行，如果孤立系统处于稳定平衡态，其熵一定是极大值： \delta S=0, \delta^2 S0,(\dfrac{\partial p}{\partial V})_{T}0,(\dfrac{\partial p}{\partial V})_{T}

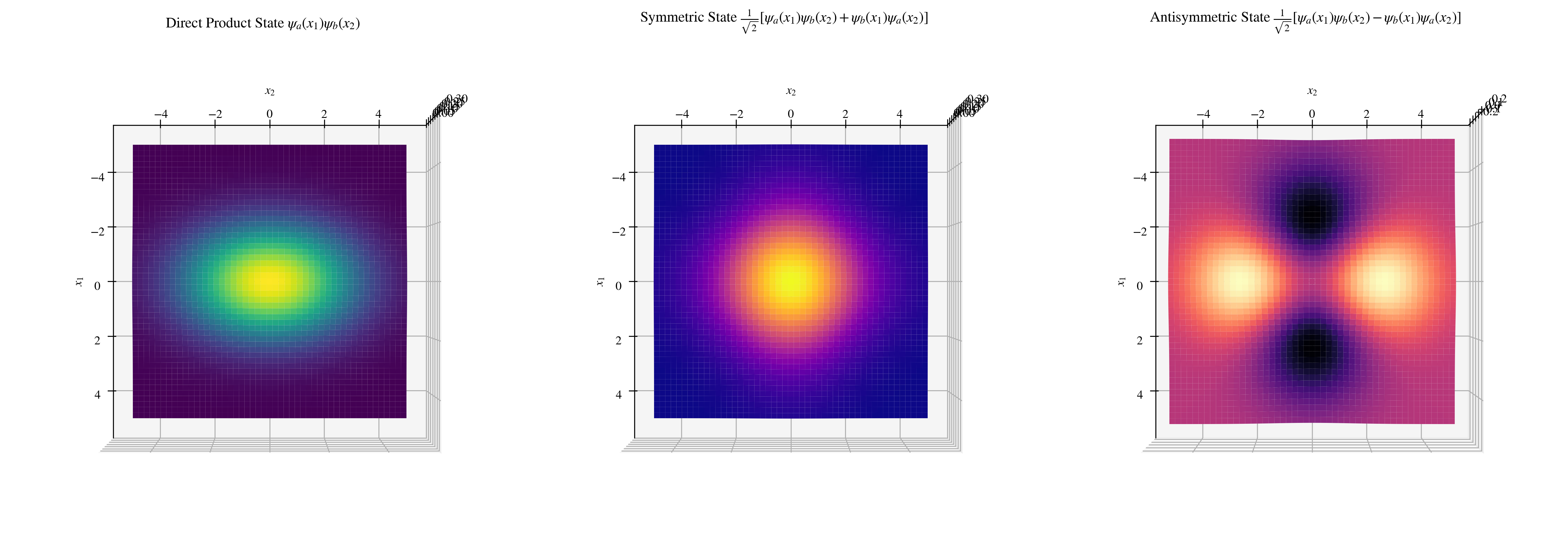
量子力学的基本假设规定基本粒子是不可区分的，不可区分的粒子即为全同粒子。当研究两个相同粒子体系的时候，不可避免涉及到相互作用的问题，为了简单起见，我们假设两个粒子没有相互作用。 波函数的交换对称性 交换力 费米子，玻色子和泡利不相容原理 元素周期表与洪特规则 自由电子气 波函数的交换对称性既然两个粒子是不可区分的，他们的波函数满足： |\psi_{1,2}|^2=|\psi_{2,1}|^2这必然要求$\psi_{1,2}=e^{i\theta}\psi_{2,1}=e^{2i\theta}\psi_{1,2}$，也即： \psi_{1,2}=\pm\psi_{2,1}这样似乎可以写出体系的波函数了： \psi(x_1,x_2)=\psi_a(x_1)\psi_b(x_2)这里似乎有几个小问题： 如果这两个态是相同的，也就是$\psi(x_1,x_2)=\psi_a(x_1)\psi_a(x_2)$，那么显然是交换对称的，不可能出现交换反对称的情况——这说明费米子不可能占据同一个态（泡利不相容原理）。 如果这两个态不相同，那为什么不写成$\psi(x_1,x_2)=\psi_b( ...

偏微分关系 热力学基本函数与方程 麦克斯韦关系 图示 一阶关系 二阶关系 一阶导处理方法 二阶导处理 所有结果一览 常数 $S$ $U$ $H$ 偏微分关系 倒易关系：$(\dfrac{\partial x}{\partial y})_z(\dfrac{\partial y}{\partial x})_z=1$ 循环关系：$(\dfrac{\partial x}{\partial y})_z(\dfrac{\partial y}{\partial z})_x(\dfrac{\partial z}{\partial x})_y=-1$ 复合关系1：$(\dfrac{\partial x}{\partial y})_w(\dfrac{\partial y}{\partial z})_w=(\dfrac{\partial x}{\partial z})_w$ 复合关系2：$(\dfrac{\partial x}{\partial y})_w=(\dfrac{\partial x}{\partial y})_z+(\dfrac{\partial x}{\partial z})_y( ...

必要的数学知识偏微分关系 倒易关系：$(\dfrac{\partial x}{\partial y})_z(\dfrac{\partial y}{\partial x})_z=1$ 循环关系：$(\dfrac{\partial x}{\partial y})_z(\dfrac{\partial y}{\partial z})_x(\dfrac{\partial z}{\partial x})_y=-1$ 复合关系1：$(\dfrac{\partial x}{\partial y})_w(\dfrac{\partial y}{\partial z})_w=(\dfrac{\partial x}{\partial z})_w$ 复合关系2：$(\dfrac{\partial x}{\partial y})_w=(\dfrac{\partial x}{\partial y})_z+(\dfrac{\partial x}{\partial z})_y(\dfrac{\partial z}{\partial y})_w$ Proof:设$f(x,y,z)=0$，则 (\dfrac{\parti ...

热力学基本方程 麦克斯韦关系 特性函数理论 基本热力学函数的确定 理想气体的热力学函数 范氏气体的热力学函数 简单固体的热力学函数 热辐射的热力学理论 磁介质的热力学 热力学基本方程dS=\frac{dQ}{T}=\frac{dU+pdV}{dT}\Rightarrow dU=TdS-pdV这就是热力学基本方程，其描述了状态参量$p,V$和态函数$T,S,U$的关系。 尽管不重要，这里我们要回顾状态参量和状态函数的区别（其实是人为的）——能确定一个平衡态的最少的几个量就是状态参量，由其作为自变量的函数就是状态函数。 这里更重要的区别是，$U,S,V$指向了增量，而$p,T$指向了平衡态的参量。 对热力学基本方程进行变量的替换可以得到另外三个具有物理意义的同本质的方程（可以并称为热力学基本方程）。 由焓的定义$H=U+pV$，可得$dU=dH-pdV-Vdp=TdS-pdV$，所以dH=TdS+Vdp 由亥姆霍兹自由能的定义$F=U-TS$，可得$dU=dF+TdS+SdT=TdS-pdV$，所以dF=-SdT-pdV 由吉布斯自由能的定义$G=H-TS$，可得$dU=dG ...

在学习统计物理之前，大概都有热力学的基础。热力学更唯像一些，归纳了四条基本规律和物态方程，这些从何而来？或许统计物理会给出一个更基本的解答。 热力学系统 系统的分类 热平衡态 热力学第零定律 温度 物态方程 气体 固体和液体 顺磁性固体 准静态过程和功 流体系统 液体薄膜 电介质 磁介质 热力学第一定律 内能、焓和热容 准静态过程和绝热过程 多方过程 热机 热力学第二定律 热力学温标 克劳修斯不等式 理想气体的熵 不可逆过程熵变的计算 自由能和吉布斯自由能 热力学第三定律 热力学系统系统的分类热力学研究大量微观粒子组成的宏观物质系统。一个热力学孤立系统，最后会达到热力学平衡状态，表现为各参量（几何参量，力学参量，化学参量，电磁参量）不变。 性质 孤立系统 封闭系统 开放系统 粒子数 不变 不变 可变 能量 不变 可变 可变 如果一个系统的各部分性质相同，那么称之为均匀系；如果不是，但可以分为若干个均匀系统之和，那么每个均匀的部分称为一个相，系统称为复相系。 热平衡态以上的讨论都是基于系统处于热平衡态。从不平衡态到平衡态，有一个弛豫 ...

我们曾在 多电子原子 中讨论过类似的定性问题。现在我们用更加定量的语言描述角动量耦合。 角动量耦合角动量之和两个电子自旋的状态可以描述为角动量相加$\hat J=\hat j_1+\hat j_2$，简单验证可知其也是角动量： [\hat J_x,\hat J_y]=[\hat j_{1x}+\hat j_{2x},\hat j_{1y}+\hat j_{2y}]=i\hbar \hat J_z角动量的描述描述角动量之和有两种方式（两种基底）： $|j_1,j_2,m_1,m_2\rangle=|j_1,m_1\rangle|j_2,m_2\rangle$ 即为非耦合基底； $|j_1,j_2,J,m\rangle$ 即为耦合基底。 我们先来验证这两种表示方式的合理性（即这四个物理量是否守恒且互相对易，构成一组CSCO）： 对于非耦合基底，显然：$[\hat{j}^2_1,\hat{j}^2_2]=0,[\hat{j}^2_1,\hat{j}_{1z}]=0,[\hat{j}^2_1,\hat{j}_{2z}]=0,[\hat{j}^2_2,\hat{j}_{1z}]=0,[\h ...

Contend 托福阅读 托福听力杂谈 托福听力题型与结构 口语语料 托福口语Task1 托福口语Task1范例 托福口语Task2 托福口语Task3 托福口语Task4 托福写作 托福写作词汇计划 托福写作范文 词以类记Content 托福首考有感

参考资料 学术写作 题型 结构 Sample 1 - Comparison Sample 2 - Evaluation Sample 3 - Argument Sample 4 - Solution 综合写作 题型 材料结构 文章结构 Sample - Opposite - TPO 40 参考资料Vince9120 学术讨论 Academic Discussion Vince9120 综合写作 Integrated Writing。此部分被UP下架，但仍有完整版视频。 学术写作第一道写作题目为学术写作（Writing for an Academic Discussion），这个新任务取代了之前的独立写作任务，旨在模拟现实情况中由老师提问、由学生主导的学术讨论。实际上和独立写作没有区别。 Time：10 minutes; Words：At least 100 words, preferably 180 words. Task： Read the questions asked by the teacher; Read the response maded by the t ...