磁性概论

磁性本质上是一种量子效应，而固体的磁性又是大量孤立原子的磁性的集体效应。按照量子力学的理论，原子的磁矩主要来源于：

  • 电子固有的自旋磁矩；
  • 电子绕核运动产生的轨道磁矩；
  • 外加磁场感生的轨道磁矩变化。

在经典图像中，前两个磁矩会跟随外场的方向，给出顺磁性的贡献，此时磁化率的大小大概在$0\sim 10^{-2}$之间，随温度的升高而降低，即居里定律：

顺磁性的计算在 玻尔兹曼统计 中也曾提到过。

如果前两个磁矩耦合后为零，那么抗磁性作为二阶效应就会显现出来，这是因为磁场给电子提供额外的离心力，致使磁矩变小，磁化率大概在$-10^{-5}\sim -10^{-6}$之间，且不随温度变化。

前两种情况都是在原子间相互作用可以忽略不计的时候，原子磁矩的取向趋于随机分布，宏观上表现为顺磁性或抗磁性。若原子间相互作用不能忽略，则会出现铁磁性、反铁磁性和亚铁磁性等现象，这些现象的本质是原子间的交换相互作用，我们常用交换相互作用常数$J$来描述。这是一个对于铁磁性$J>0$，对于反铁磁性$J<0$的量。

image.png

孤立原子的磁矩

无外场情况

在计算孤立原子的磁矩之前，我们得复习一下量子力学中自旋和轨道角动量的耦合（ 原子的精细结构 ）：

以及洪特规则（ 全同粒子 ）：

  • 第一规则：总自旋$S$越大，能量越低；
  • 第二规则：给定自旋$S$的情况下，总轨道角动量$L$越大，能量越低。
  • 第三规则：给定自旋$S$和轨道角动量$L$的情况下，如果未填满半壳层，总角动量$J=|L-S|$；总角动量$J=|L+S|$。

对于基态铁原子，即$3d^6$电子组态，按照洪特规则可知$S=2$，$L=2$，$J=4$，即$^5D_4$态。由此可计算出其朗德因子为$g_j=1.5$，磁矩为：

这个磁矩被称为固有磁矩，与我们下面所说的饱和磁矩有所区别。

原子磁矩对外场的响应

先不考虑自旋，写出孤立原子在外磁场下的哈密顿量，假设$\vec{B}=B\hat{z}$：

根据微扰论，可得一阶能量修正为：

根据热力学的结果，可知磁矩为：

从这里就可以看到顺磁性和抗磁性的来源。顺磁性来源于轨道磁矩在外磁场中产生塞曼效应，能量简并消失，所以原子磁矩趋向于与外场同向，最大值为饱和磁矩$m\mu_B$；抗磁性的磁矩则永远小于零，说明与磁场反向。

抗磁性

前面已经计算出了抗磁性部分的磁矩，可以得到磁化率为：

对于抗磁性固体，不考虑原子间的相互作用，磁化率为：

一般来说，具有饱和电子结构的原子或离子构成的固体，如惰性气体、许多有机化合物、部分金属和非金属单质、许多离子晶体都是抗磁性的。

顺磁性

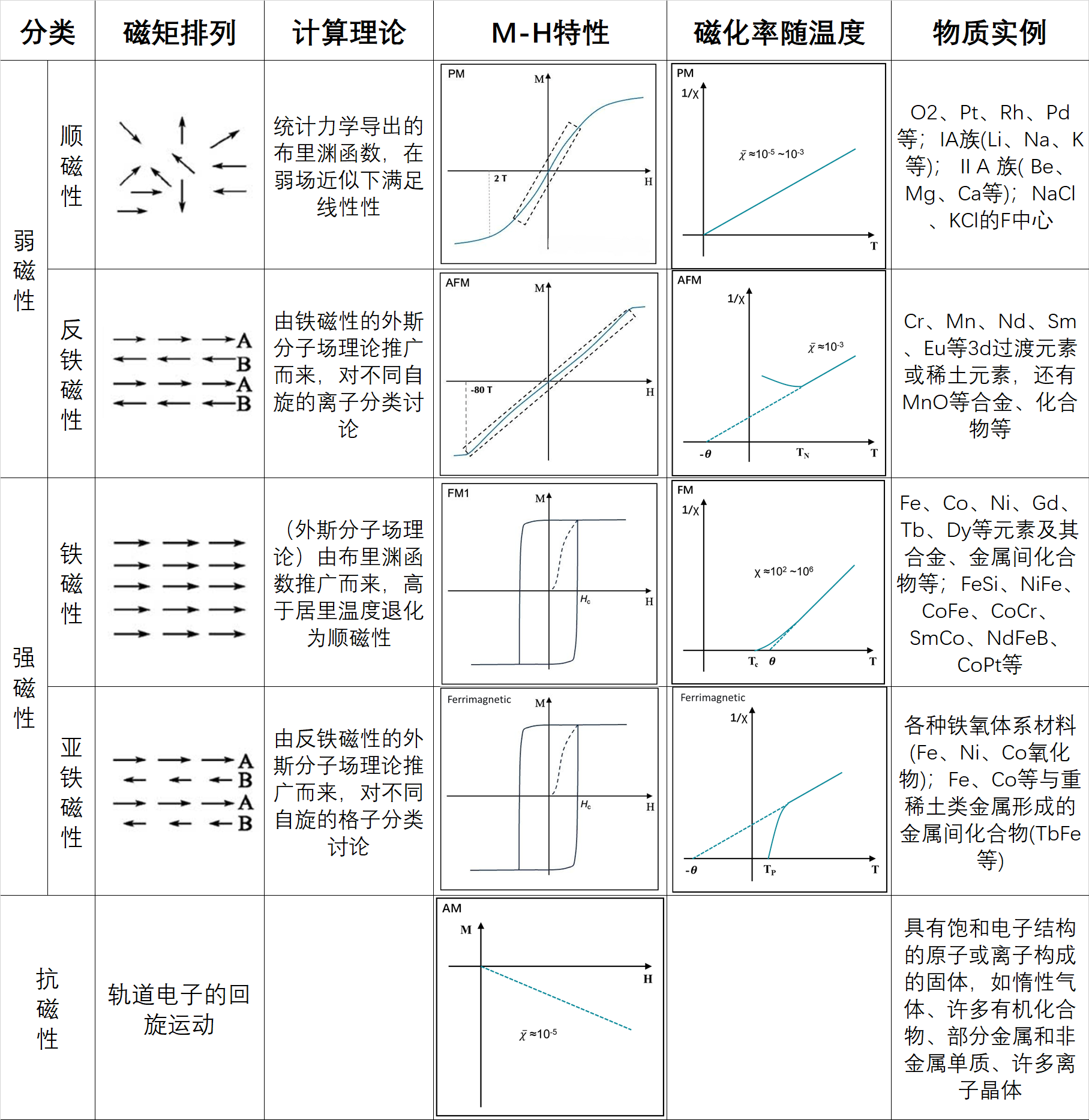
在 玻尔兹曼统计 中，我们计算了$J=\frac12$时的顺磁性，现在我们推广为任意$J$：

这说明总的磁矩体现为最大磁矩$\mu_{max}=g_J\mu_BJ$与布里渊函数$B_J(x)$的乘积，其中$B_J(x)$为布里渊函数：

image.png

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体（可选）
# Set the font family to SimHei (黑体)
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

# 定义coth函数（numpy没有内置）
def coth(x):
    return 1/np.tanh(x)

# 定义布里渊函数
def brillouin_function(x, J):
    if J == float('inf'):
        return coth(x) - 1/x
    else:
        term1 = (2*J + 1)/(2*J) * coth((2*J + 1)/(2*J) * x)
        term2 = 1/(2*J) * coth(1/(2*J) * x)
        return term1 - term2

# 创建图形
plt.figure(figsize=(12, 6))

# 第一子图：布里渊函数
plt.subplot(1, 2, 1)
x = np.linspace(-6, 6, 1000)
J_values = [0.5, 1, 2, float('inf')]
labels = ['J = 1/2', 'J = 1', 'J = 2', 'J = ∞']

for J, label in zip(J_values, labels):
    y = brillouin_function(x, J)
    plt.plot(x, y, label=label, linewidth=2)

plt.xlabel('x = g_J μ_B B/(k_B T)')
plt.ylabel('B_J(x)')
plt.title('布里渊函数')
plt.legend()
plt.grid(True, alpha=0.3)
plt.xlim(-6, 6)
plt.ylim(-1.1, 1.1)

# 第二子图：磁矩μ
plt.subplot(1, 2, 2)
J_values = [0.5, 1, 1.5]
labels = ['J = 1/2', 'J = 1', 'J = 3/2']

for J, label in zip(J_values, labels):
    # μ = g_J * μ_B * J * B_J(x)
    # 这里我们归一化处理，只绘制B_J(x)
    mu =J* brillouin_function(x, J)
    plt.plot(x, mu, label=label, linewidth=2)

plt.xlabel('x = g_J μ_B B/(k_B T)')
plt.ylabel('μ/(g_J μ_B J)')
plt.title('磁矩与磁场和温度的关系')
plt.legend()
plt.grid(True, alpha=0.3)
plt.xlim(-6, 6)
plt.ylim(-1.6, 1.6)

plt.tight_layout()
plt.show()

可以看到，当满足弱场高温条件时，磁化率与温度成反比，这就是居里定律：

与磁场无关。当满足强场低温条件时，磁矩趋于饱和，达到最大值$g_J\mu_BJ$。

该理论的局限性：

  • 忽略了原子间的相互作用；
  • 忽略了激发态的影响

内层没有被填满的自由原子或离子，如过渡金属元素和稀土元素，通常具有较大的顺磁性。

轨道猝灭效应

实验表明，过渡金属元素的顺磁性小于理论值$\mu_{coup}=2\sqrt{J(J+1)}\mu_B$，且更接近于自旋理论值$\mu_{spin}=2\sqrt{S(S+1)}\mu_B$，而不是轨道部分$\mu_{orb}= \sqrt{L(L+1)}\mu_B$。这是因为除了s电子外，其他电子的波函数都是花瓣状。尽管在上述讨论中，中心势场保证了$\hat L_z$是守恒的，但在实际情况中，晶体内部存在强各向异性场，破坏了中心势场的对称性，导致$\hat L_z$不再是守恒量，轨道角动量被猝灭。

对于铁族过渡元素离子，3d电子是最外层的电子，所以轨道猝灭效应最明显；而稀土金属的4f电子被$5s^2p^6d^{10}6s^2$屏蔽，轨道猝灭效应较弱。

我们举个例子来解释轨道猝灭效应。考虑一个简单的非中心势场：

C系数是由于势场的Laplace方程决定的。考虑三种p电子轨道：

显然，非对角矩阵元为零：

对角矩阵元为：

考虑到$\langle x^4\rangle=3\langle x^2y^2\rangle$，所以$I_1>I_2$。最终简并能级劈裂3个能级，且$\psi_z$对应的能量最低（若$A,B>0$）。

此时，虽然轨道量子数$l=1$仍然不变，但是$m_l$不再是好的量子数：

如果是中心势场，那么简并导致的线性组合就能让$m_l$成为好的量子数。

固体的磁性

上述讨论了孤立原子的磁性来源，但固体作为一个集体系统，有些效应是不可避免的。我们重新审视顺磁性、抗磁性，以及从原子相互作用引申出铁磁性、反铁磁性。

泡利顺磁性

上文使用玻尔兹曼分布得到了孤立原子的顺磁性。但是在固体中，外围自由电子是满足费米-狄拉克分布的，是强简并的。费米球内部的电子无法反转自旋，只有费米面附近的电子才能响应外场，这就是泡利顺磁性。我们曾在 金属电子论 中提到了唯象的计算，事实上，只需要把玻尔兹曼分布换成费米-狄拉克分布就可以得到一样的结果：

其中系数$\frac32$来源于对态密度$\sqrt{E}$的积分。

朗道抗磁性

上文提到抗磁性来源于电子轨道在外磁场下的能量修正，或者说，在经典图像下，电子回旋速度降低，表现为抗磁性。而在固体中，由于电子简并，电子的轨道运动会发生量子化，这就是朗道能级（ Quantum Dynamics & Quantum Geometry ）。由此产生朗道抗磁性：

可以发现，朗道抗磁性是泡利顺磁性的$-\frac13$，所以金属的总磁化率为：

如果考虑内层电子的抗磁性，那么实际的磁化率会更小一些。

铁磁性

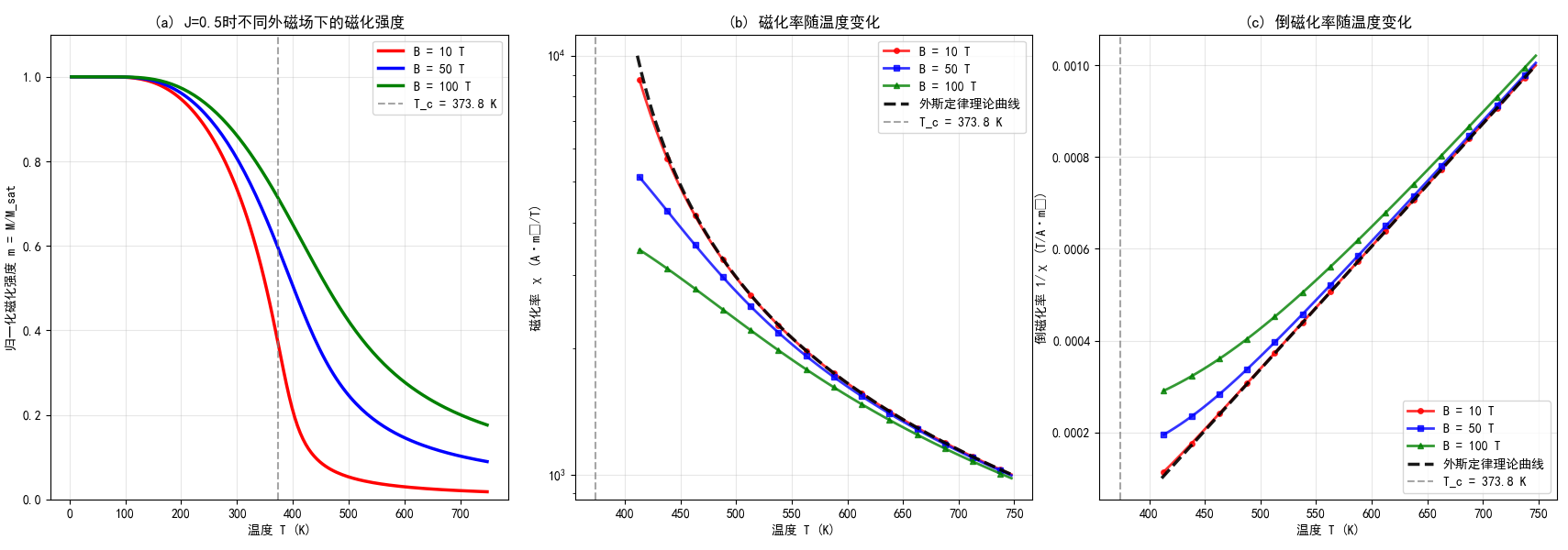
实验事实表明，铁、钴、镍等金属在磁场$B=0$时也能表现出自发磁化现象，即$M\neq 0$。随着温度的升高，磁化强度逐渐减小，在某一临界温度（铁磁居里温度）$T_C$时突然变为零。随着温度继续升高，磁化率近似满足居里-外斯定律：

这里的$\theta$称为顺磁居里温度。一般来说，顺磁居里温度$\theta$稍微大于铁磁居里温度$T_C$。不过在下面的外斯分子场理论中，由于使用平均场理论，忽略了磁涨落，我们会发现$\theta=T_C$。

外斯分子场理论

在顺磁性的讨论中，我们可以得到磁化强度和外磁场的关系：

若要讨论铁磁性，即考虑原子间的相互作用，我们考虑一个平均场来表征其效果：

代入上式，可得：

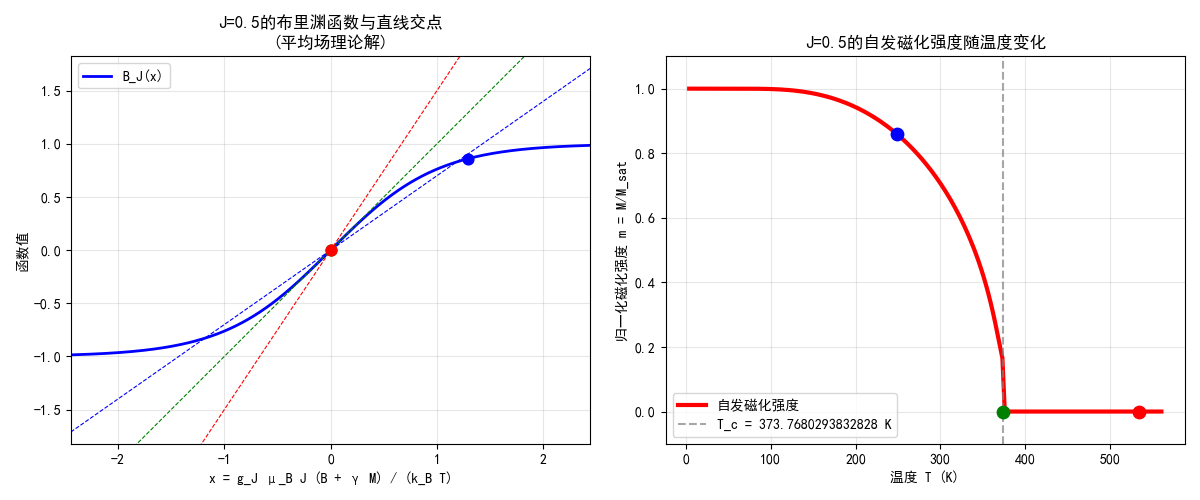
这是一个超越方程，不过总是可解的。先考虑无外场情况$B=0$：

这是布里渊函数与经过原点的直线，二者交点即为磁化强度。考虑到布里渊函数是导数单调递减的，在外场为零时，至多只有一个非零解，且高于居里温度的只有零点解。我们可以通过数值计算：

image.png

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

# 定义coth函数和布里渊函数
def coth(x):
    return 1 / np.tanh(x)

def brillouin_function(x, J):
    if J == float('inf'):
        return coth(x) - 1 / x
    else:
        term1 = (2 * J + 1) / (2 * J) * coth((2 * J + 1) / (2 * J) * x)
        term2 = 1 / (2 * J) * coth(1 / (2 * J) * x)
        return term1 - term2


# 物理常量与参数
J = 0.5
g_J = 2.0
mu_B = 9.274e-24
k_B = 1.380649e-23
N = 6e28
gamma = 0.001
M_sat = N * g_J * mu_B * J
B_J_prime_0 = (J + 1) / (3 * J)
def calculate_Tc(gamma, N, J, g_J):
    numerator = gamma * N * J * (J + 1) * (g_J * mu_B) ** 2
    Tc = numerator / (3 * k_B)
    return Tc
T_c = calculate_Tc(gamma, N, J, g_J)


def solve_spontaneous_magnetization(T, J, gamma, max_iter=200, tol=1e-10):
    if T >= T_c:
        return 0.0
    alpha = N * g_J ** 2 * mu_B ** 2 * J ** 2 * gamma / (k_B * T)
    m = 0.9
    for _ in range(max_iter):
        x = alpha * m
        m_new = brillouin_function(x, J)
        if abs(m_new - m) < tol:
            return m_new
        m = 0.7 * m + 0.3 * m_new
    return m


print(f"J = {J}")
print(f"布里渊函数在x=0处的导数 B_J'(0) = {B_J_prime_0:.4f}")
print(f"临界温度 T_c = {T_c} K")


plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
x_range = np.linspace(-4, 4, 2000)
B_J = np.array([brillouin_function(x, J) for x in x_range])
plt.plot(x_range, B_J, 'b-', linewidth=2, label=f'B_J(x)')
slopes = [1.5, 1.0, 0.7]
colors = ['red', 'green', 'blue']
for slope, color in zip(slopes, colors):
    plt.plot(x_range, slope * x_range, color=color, linestyle='--', linewidth=0.8)
temps_from_slopes = [T_c / s for s in slopes]
m_from_slopes = []
x_from_slopes = []
for T_val, s in zip(temps_from_slopes, slopes):
    m_val = solve_spontaneous_magnetization(T_val, J, gamma)
    m_from_slopes.append(m_val)
    M_val = m_val * M_sat
    x_val = (g_J * mu_B * J * gamma * M_val) / (k_B * T_val) if T_val != 0 else 0.0
    x_from_slopes.append(x_val)
colors=['blue', 'green', 'red']
for s, T_val, m_val, x_val, color in zip(slopes, temps_from_slopes, m_from_slopes, x_from_slopes, colors):
    plt.scatter(x_val, m_val, color=color, s=60, zorder=5)
    print(f"斜率 {s} -> 温度 T = {T_val:.6g} K, m = {m_val:.6f}, x = {x_val:.6f}")
plt.xlabel('x = g_J μ_B J (B + γ M) / (k_B T)')
plt.ylabel('函数值')
plt.title(f'J={J}的布里渊函数与直线交点\n(平均场理论解)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.axis('equal')
plt.xlim(-2, 2)
plt.ylim(-1.5, 1.5)


plt.subplot(1, 2, 2)
T_values = np.linspace(0.01 * T_c, 1.5 * T_c, 200)
M_values = [solve_spontaneous_magnetization(T, J, gamma) for T in T_values]
plt.plot(T_values, M_values, 'r-', linewidth=3, label='自发磁化强度')
plt.axvline(x=T_c, color='gray', linestyle='--', alpha=0.7, label=f'T_c = {T_c} K')
plt.xlabel('温度 T (K)')
plt.ylabel('归一化磁化强度 m = M/M_sat')
plt.title(f'J={J}的自发磁化强度随温度变化')
plt.legend()
plt.grid(True, alpha=0.3)
plt.ylim(-0.1, 1.1)
for s, T_val, m_val, x_val, color in zip(slopes, temps_from_slopes, m_from_slopes, x_from_slopes, colors):
    plt.scatter([T_val], [m_val], color=color, s=80, zorder=5)
plt.tight_layout()
plt.show()

其中，铁磁居里温度是很好计算的：

对于外磁场不为零的情况，我们可以在弱场极限下推导出外斯定律。考虑弱场极限：

可以看到，这里的居里温度$\theta=T_C$。

image.png

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

# 定义coth函数和布里渊函数
def coth(x):
    return 1 / np.tanh(x)

def brillouin_function(x, J):
    if J == float('inf'):
        return coth(x) - 1 / x
    else:
        term1 = (2 * J + 1) / (2 * J) * coth((2 * J + 1) / (2 * J) * x)
        term2 = 1 / (2 * J) * coth(1 / (2 * J) * x)
        return term1 - term2

# 物理常量与参数
J = 0.5
g_J = 2.0
mu_B = 9.274e-24
k_B = 1.380649e-23
N = 6e28
gamma = 0.001
M_sat = N * g_J * mu_B * J
B_J_prime_0 = (J + 1) / (3 * J)

def calculate_Tc(gamma, N, J, g_J):
    numerator = gamma * N * J * (J + 1) * (g_J * mu_B) ** 2
    Tc = numerator / (3 * k_B)
    return Tc

T_c = calculate_Tc(gamma, N, J, g_J)

# 修改求解函数以包含外磁场
def solve_magnetization(T, J, gamma, B_ext, max_iter=500, tol=1e-10):
    """求解给定温度和外磁场下的磁化强度"""
    alpha = N * g_J ** 2 * mu_B ** 2 * J ** 2 * gamma / (k_B * T)
    beta = g_J * mu_B * J * B_ext / (k_B * T)
    
    # 初始猜测
    m = 0.9 if T < T_c else 0.1
    
    for _ in range(max_iter):
        x = alpha * m + beta
        m_new = brillouin_function(x, J)
        if abs(m_new - m) < tol:
            return m_new
        m = 0.7 * m + 0.3 * m_new  # 松弛迭代
    
    return m

# 定义外斯定律的磁化率函数
def weiss_law_susceptibility(T, T_c, C):
    """外斯定律：χ = C / (T - T_c)"""
    # 处理数组输入
    T = np.asarray(T)
    result = np.zeros_like(T)
    
    # 对于T <= T_c的情况，设为无穷大（或一个很大的数用于绘图）
    mask = T <= T_c
    result[mask] = 1e20  # 用一个很大的数代替无穷大
    
    # 对于T > T_c的情况，应用外斯定律
    result[~mask] = C / (T[~mask] - T_c)
    
    return result

# 计算居里常数C
C = (N * g_J**2 * mu_B**2 * J * (J + 1)) / (3 * k_B)

print(f"J = {J}")
print(f"布里渊函数在x=0处的导数 B_J'(0) = {B_J_prime_0:.4f}")
print(f"临界温度 T_c = {T_c:.2f} K")
print(f"居里常数 C = {C:.6e}")

# 创建三子图
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20, 6))

# 不同外磁场值（去掉B=0，因为磁化率在B=0时发散）
B_values = [10, 50, 100]  # 特斯拉
colors = ['red', 'blue', 'green']
markers = ['o', 's', '^']
B_labels = [f'B = {B} T' for B in B_values]

# 温度范围
T_values = np.linspace(0.01 * T_c, 2.0 * T_c, 150)

# 左图：磁化强度 vs 温度
for B_ext, color, label in zip(B_values, colors, B_labels):
    M_values = []
    for T in T_values:
        m_val = solve_magnetization(T, J, gamma, B_ext)
        M_values.append(m_val)
    
    ax1.plot(T_values, M_values, color=color, linewidth=2.5, label=label)

ax1.axvline(x=T_c, color='gray', linestyle='--', alpha=0.7, label=f'T_c = {T_c:.1f} K')
ax1.set_xlabel('温度 T (K)')
ax1.set_ylabel('归一化磁化强度 m = M/M_sat')
ax1.set_title(f'(a) J={J}时不同外磁场下的磁化强度')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax1.set_ylim(0, 1.1)

# 中图：磁化率 vs 温度
for B_ext, color, marker, label in zip(B_values, colors, markers, B_labels):
    susceptibility_values = []
    
    for T in T_values:
        if T > T_c + 0.1 * T_c:  # 避免T_c附近的数值不稳定
            # 数值计算的磁化率：χ = M/B
            M_val = solve_magnetization(T, J, gamma, B_ext)
            chi_val = M_val * M_sat / B_ext
            susceptibility_values.append(chi_val)
        else:
            susceptibility_values.append(float('inf'))
    
    # 过滤掉无穷大值用于绘图
    T_valid = T_values[T_values > T_c + 0.1 * T_c]
    chi_valid = np.array(susceptibility_values)[T_values > T_c + 0.1 * T_c]
    
    # 绘制数值计算的磁化率
    ax2.plot(T_valid, chi_valid, color=color, marker=marker, markersize=4, 
             linewidth=2, label=label, alpha=0.8, markevery=5)

# 绘制外斯定律理论曲线（弱场极限理论值）
T_weiss = np.linspace(T_c + 0.1 * T_c, 2.0 * T_c, 100)
weiss_chi_values = weiss_law_susceptibility(T_weiss, T_c, C)
ax2.plot(T_weiss, weiss_chi_values, 'k--', linewidth=2.5, 
         label='外斯定律理论曲线', alpha=0.9)

ax2.axvline(x=T_c, color='gray', linestyle='--', alpha=0.7, label=f'T_c = {T_c:.1f} K')
ax2.set_xlabel('温度 T (K)')
ax2.set_ylabel('磁化率 χ (A·m²/T)')
ax2.set_title('(b) 磁化率随温度变化')
ax2.legend()
ax2.grid(True, alpha=0.3)
ax2.set_yscale('log')  # 使用对数坐标更好地显示发散行为

# 右图：倒磁化率 vs 温度
for B_ext, color, marker, label in zip(B_values, colors, markers, B_labels):
    inverse_susceptibility_values = []
    T_inverse_valid = []
    
    for T in T_values:
        if T > T_c + 0.1 * T_c:  # 避免T_c附近的数值不稳定
            # 数值计算的磁化率：χ = M/B
            M_val = solve_magnetization(T, J, gamma, B_ext)
            chi_val = M_val * M_sat / B_ext
            if chi_val > 0:  # 确保磁化率为正
                inverse_chi = 1 / chi_val
                inverse_susceptibility_values.append(inverse_chi)
                T_inverse_valid.append(T)
    
    # 绘制倒磁化率
    ax3.plot(T_inverse_valid, inverse_susceptibility_values, color=color, marker=marker, 
             markersize=4, linewidth=2, label=label, alpha=0.8, markevery=5)

# 绘制外斯定律的理论倒磁化率曲线
T_inverse_weiss = np.linspace(T_c + 0.1 * T_c, 2.0 * T_c, 100)
weiss_inverse_chi = (T_inverse_weiss - T_c) / C  # 直接计算，避免函数调用问题
ax3.plot(T_inverse_weiss, weiss_inverse_chi, 'k--', linewidth=2.5, 
         label='外斯定律理论曲线', alpha=0.9)
ax3.axvline(x=T_c, color='gray', linestyle='--', alpha=0.7, label=f'T_c = {T_c:.1f} K')
ax3.set_xlabel('温度 T (K)')
ax3.set_ylabel('倒磁化率 1/χ (T/A·m²)')
ax3.set_title('(c) 倒磁化率随温度变化')
ax3.legend()
ax3.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

磁滞回线与磁晶的各向异性

实验事实表明，在铁磁材料中，磁化强度$M$与外磁场$B$并非简单的函数关系，而是存在滞后现象，即磁滞回线。使用外斯的分子场理论其实可以解释磁滞现象，但需要引入一些假定。

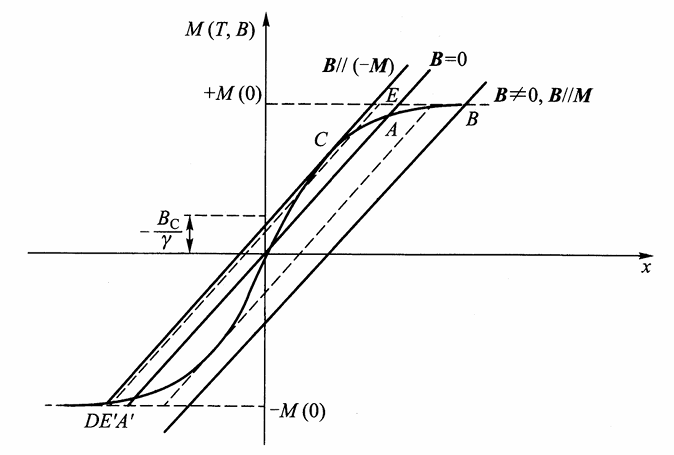
image.png

假设最初材料放置在没有外场的环境中，此时直线与布里渊函数交于$A,A’$两点，假设材料的磁化强度为$M_A$。当施加一个小的正外场时，布里渊函数上移，交点变为$B$，此时磁化强度变为$M_B>M_A$。如果施加一个反向的小外场，看上去有两个交点$E,E’$，但实际上由于$E’$和外场平行，系统会跳变到$E’$点，这和我们观测到实验中存在矫顽力的事实不符，这说明$E,E’$两个暂稳态中存在较大的势垒。

外斯分子场作为各向同性的平均场，无法解释势垒的存在。实际上，由于晶体的结构本身是各向异性的，会发生轨道角动量猝灭，由于自旋轨道耦合，自旋在空间中有着优选方向（称为易轴），这就是磁晶各向异性。

我们使用一个简单的单畴磁晶来解释磁滞现象。假设单畴位于二维平面，存在易轴$\theta=0$。外场$H$与易轴夹角为$\theta$，磁晶各向异性能量系数为$k>0$，假设磁化强度与易轴的夹角为$\phi$，则总能量为：

对$\phi$求导并令其为0，得到：

解出$\phi$，即可得到给定磁化强度大小的情况下，磁化强度方向的变化规律。这说明能量函数为$E(H,\theta,M)$。

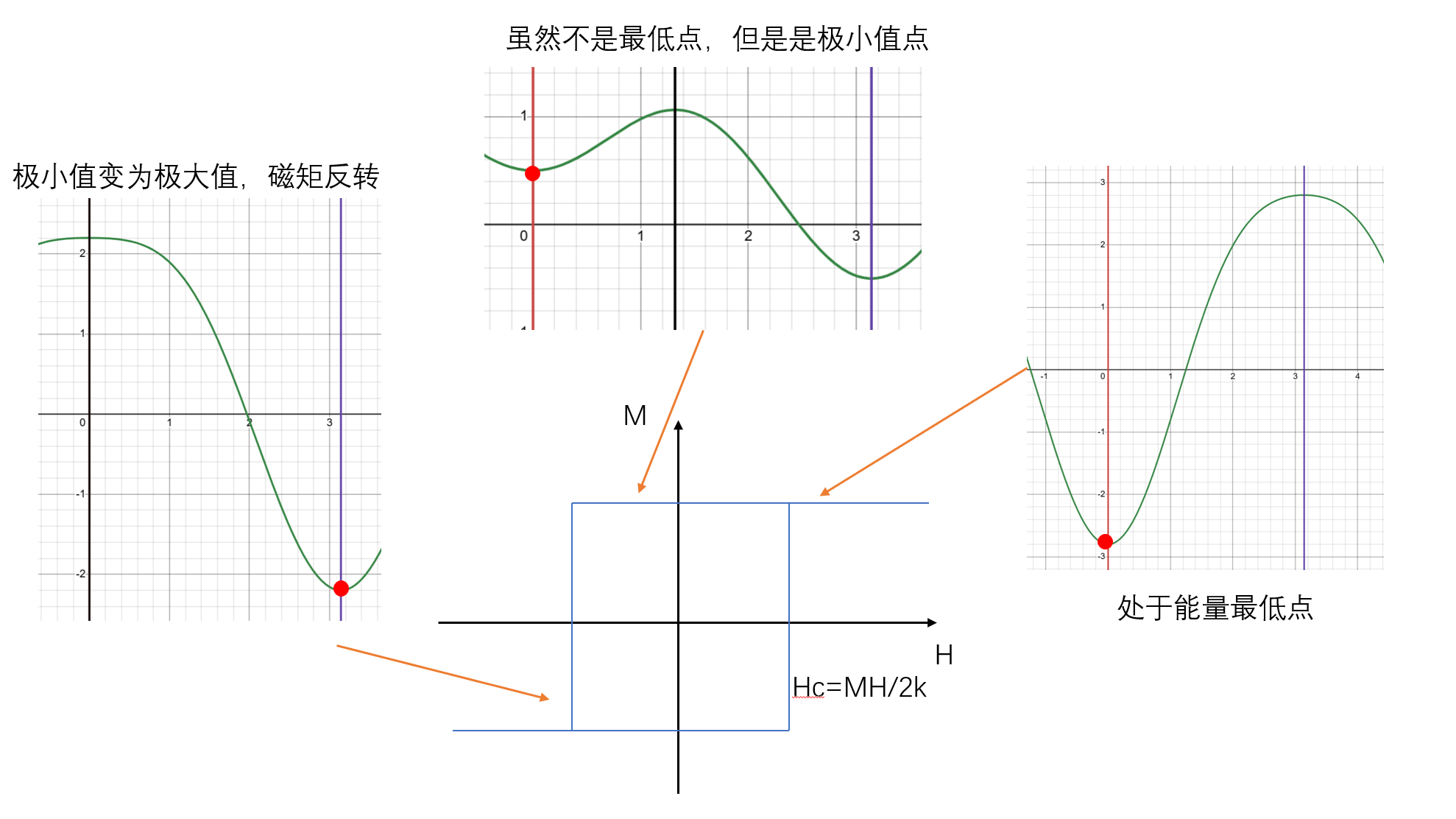
考虑外场沿易轴方向，即$\theta=0$，则有：

解得：

所以有3个解：$\phi=0,\quad\pi,\quad \arccos\left(-\dfrac{MH}{2k}\right)$。可以发现第三个解就是所谓的势垒（因为他是非易轴方向）。只有当第三个解消失时，系统才会发生跳变，这时有：

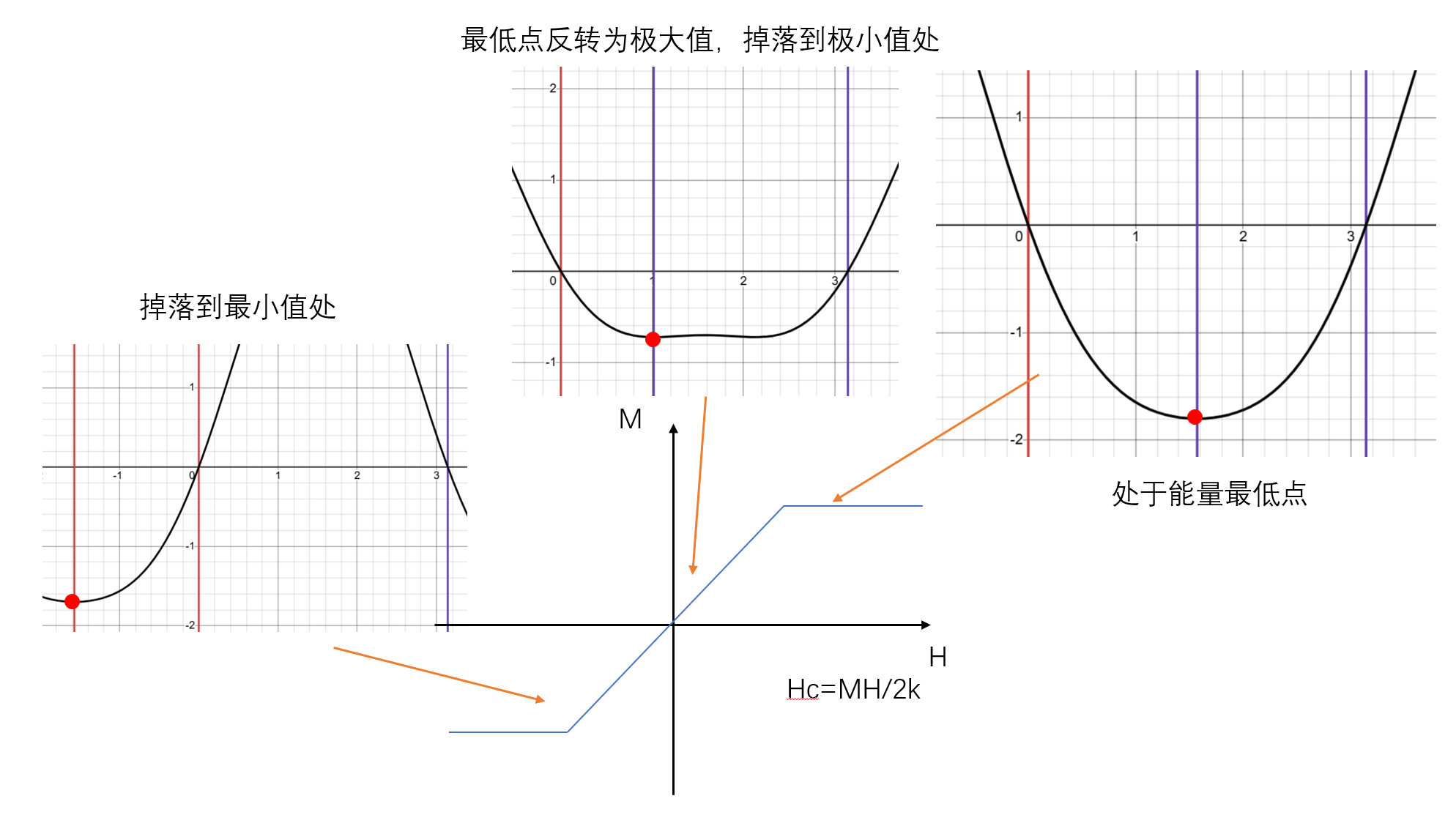
image.png

若外场沿难轴方向，即$\theta=\frac{\pi}{2}$，则有：

解得：

所以有2个解：$\phi=\dfrac{\pi}{2},\quad\arcsin\left(\dfrac{MH}{2k}\right)$。可以发现没有势垒，所以没有磁滞现象（矫顽力为0），磁化强度会连续变化，直到$H=\dfrac{2k}{M}$时达到饱和。

image.png

Heisenberg模型

外斯分子场理论虽然能很好地解释铁磁性，但它是一个唯象模型，无法解释原子间相互作用的本质。人们最初以为，磁矩之间的磁相互作用是分子场的来源，但计算表明，磁偶极子之间的相互作用太弱，无法解释铁磁性。量子力学的发展使我们认识到，电子的交换相互作用才是磁性的重要来源：

Heisenberg提出了Heisenberg模型来描述这种相互作用：

一般来说，Heisenberg模型指的是考虑各向同性的最近邻交换相互作用：

其具有以下变体：

  • 各向异性的Heisenberg模型：
  • Ising模型（$J_x=J_y=0$）：
  • XY模型（$J_z=0,J_x=J_y=J_\perp$）：

Stoner模型

如何判断一个金属是铁磁性还是顺磁性？我们可以使用Stoner模型。考虑外场下的无自发磁化的系统，由于外场的作用，顺磁态的能量较低，这导致部分逆磁态电子跃迁到顺磁态，系统能量降低为：

对于没有外场的情况，如果一个系统想要发生自发磁化，那么上述过程是逆过来的，也就是说系统的能量是增加的。为了解释铁磁性，Stoner引入交换相互作用，这样反转的电子会有一个降低的势能。我们引入一个简单的海森堡模型：

考虑平均场：

考虑：

解得：

代入海森堡模型：

相比于$\delta N=0$的情况，能量的变化为：

所以发生自发磁化的条件为：

这就是Stoner判据。其物理意义在于，如果电子交换作用$U$和态密度$N(E_F)$占据主导地位，那么电子跃迁到顺磁态形成的外场导致的势能下降会大于电子跃迁能带上的能量增加。

但是以上理论是基于能带的。对于稀土金属的$4f$电子，其被$5s^2p^6d^{10}6s^2$屏蔽，所以不允许直接交换作用。Ruderman-Kittel-Kasuya-Yosida提出$4f$电子是完全局域的，但$6s$电子是游动的，可以作为传导电子。$4f$电子和$6s$电子可以发生交换作用，使$6s$电子极化，进而对另一个地方的$4f$电子自旋取向产生影响。

铁磁自旋波

尽管外斯的分子平均场理论很好解释了$TT_C$时的顺磁性，但它忽略了自旋涨落的影响，这导致其对低温磁化和临界点附近的行为是预测不准的。更详细地说，如果使用外斯理论计算低温下的磁化强度，会发现：

这说明当温度趋近于0时，磁化强度的变化是指数趋于饱和的。但实验事实表明，磁化强度的变化呈现布洛赫$T^{3/2}$幂律：

这不是一个陌生的现象。还记得我们在 晶格动力学 中讨论的爱因斯坦模型和德拜模型吗？其实分别对应了光学支声子和声学支声子：

  • 爱因斯坦模型将光学支声子的频率视为常数，从而导致了能隙激发——一个声子想要被激发，必须获得一定的能量。这样算出的热容就是指数形式的；
  • 德拜模型考虑了声学支声子，频率随着波矢线性增加，这是一种无能隙激发模式。这样算出的热容就是幂律形式的。

所以我们可以合理猜测，导致外斯理论失败的原因是忽略了自旋波这种无能隙激发模式。如何产生无能隙激发模式呢？依旧回想声子的产生——如果仅是一个粒子的振动，肯定是需要能量的；但声子作为一种集体激发的准粒子，当$\vec{k}=0$的时候对应整体平移，是不需要消耗能量的。同样的道理，单个自旋的翻转需要消耗$8JS^2\hbar^2$的能量，但是如果是集体的自旋波激发，当波矢$\vec{k}\to 0$时，对应整体自旋的转动，是不需要能量的。

这其实隐含了戈德斯通定理：在自发对称性破缺的系统中，总会存在无能隙的激发模式。声子对应的是平移对称性的破缺，自旋波对应的是自旋旋转对称性的破缺。

image.png

认识到自旋波之后，下一步就是计算自旋波的色散关系，或者说相邻自旋之间的相互作用。我们写出heisenberg模型的哈密顿量：

利用海森堡运动方程：

仅考虑一维的最近邻相互作用：

在低温条件下，假设自旋主要沿$z$方向取向，即$S^z_i\approx \hbar S,\quad S^x_i,S^y_i\ll S$，则可以将上述方程线性化：

可以发现这个方程组和声子格波的方程$m\ddot{u}_l=\beta(u_{l+1}+u_{l-1}-2u_l)$很接近了，我们假设自旋波的解也是格波：

代入得到：

方程有解的条件是行列式为0：

解得：

与 晶格动力学 中声子的色散关系相比，可以发现：

  • 一维声子色散关系：
  • 一维自旋波色散关系：可以看到两者形式非常相似，区别在于声子是经典牛顿方程，位移对时间二阶导；而自旋波源于薛定谔方程，角动量对时间一阶导。此事在反常扩散中亦有记载。

反铁磁性

实验事实表明，铂、猛、铬等3d过渡金属元素或稀土元素的磁化率在温度$TT_N$的时候，磁化率随温度的上升而减小，且满足奈耳定律：

其中$\theta>0$。这种材料称为反铁磁材料，$T_N$称为奈耳温度。当低于奈耳温度时，材料内部的磁矩自发地排列成相邻磁矩反向取向的结构。

双子格模型

和铁磁模型一样，我们引入平均场，只不过由于反平行的存在，我们需要对不同位置的离子收到的平均场进行分类讨论（对于一维反铁磁自旋波，我们即将有类似的讨论）。以最简单的单元素简单立方点阵为例，设自旋向上的离子位于A子格，自旋向下的离子位于B子格。则不同离子受到的平均场为：

其中$\beta$表示最近邻的反铁磁交换作用，$\alpha$表示次近邻的反铁磁交换作用，则有$\beta>|\alpha|>0>\alpha$。

套用外斯分子场理论的方程组：

奈耳定律

我们讨论外场为0的情况，使用高温近似线性化布里渊函数：

设$N_A=N_B$，记：

（这个系数我们在铁磁性的结果中也曾看到过：$T_c=C\gamma$）该方程有非零解的临界条件是行列式为0：

解得奈耳温度：

这说明大于奈耳温度时，只有零解，即无自发磁化；小于奈耳温度时，有非零解，即存在子格子的自发磁化，但总磁化强度为0。

现在引入弱场来计算磁化率，总的磁化强度为：

解得：

这里的临界温度为：

反铁磁自旋波

同样需要分两种原子讨论$S^z_i\approx \hbar S,\quad S^x_i,S^y_i\ll S$，结合前面得到的$v=ue^{-i\pi/2}=-iu$：

解行列式：

解得：

亚铁磁性

亚铁磁性是介于铁磁性和反铁磁性之间的一种磁性形式。亚铁磁材料中，磁矩在不同子格中并非完全反平行排列，而是存在一定的强度差异，导致总磁化强度不为零。典型的亚铁磁材料包括氧化铁（Fe3O4）等。

尖晶石结构

常见的铁氧体按晶格类型可分为：

  • 尖晶石结构
  • 石榴石结构
  • 磁铅石结构

在这里，我们仅讨论尖晶石结构。尖晶石结构得名于镁铝尖晶石（$MgAl_2O_4$），其化学通式可以写为：

其中$X^{2+}$表示二价阳离子，$Y^{3+}$表示三价阳离子。尖晶石结构中，一个晶胞包含了8个分子式，如图由两种结构组成：

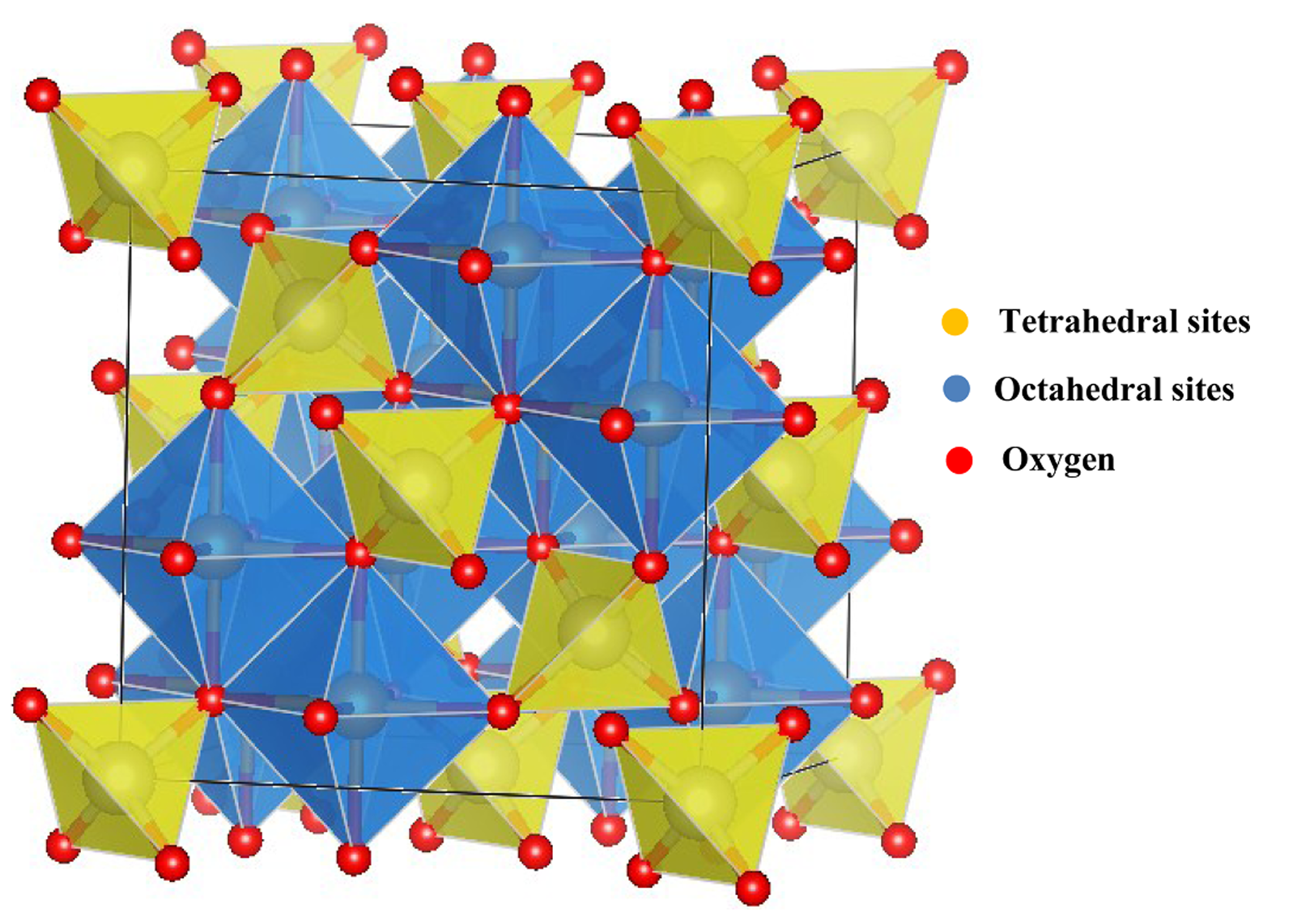
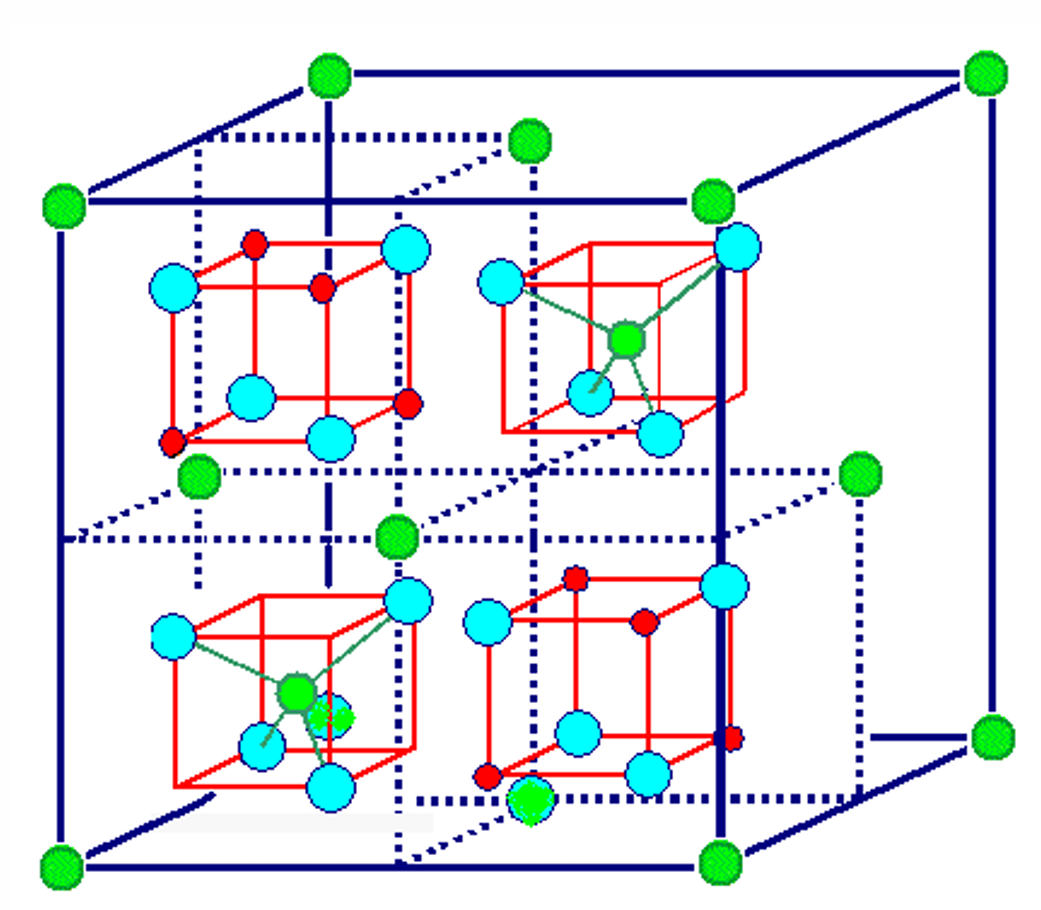
image.png

image.png

假设有$\lambda$份的$X^{2+}$占据了四面体位置，有$\mu$份的$X^{2+}$占据了八面体位置，则化学通式可以写为：

其中$\lambda+\mu=1$。当$\lambda=1,\mu=0$时，称为正常尖晶石结构；当$\lambda=0,\mu=1$时，称为反尖晶石结构。

根据平均场理论，AB结构离子的平均场分别为：

设$\gamma_{AB}=\gamma_{BA}=\gamma$，$a=\dfrac{\gamma_{AA}}{\gamma},\quad b=\dfrac{\gamma_{BB}}{\gamma}$，则有：

使用类似的方法，不难得到：

  • 临界温度：解行列式为0： 解得：

当$\lambda=1,\mu=0$时，$T_c=C\gamma a$，对应正常尖晶石结构；当$\lambda=0,\mu=1$时，$T_c=C\gamma b$，对应反尖晶石结构。这个临界温度的样式和此前是差不多的。

  • 居里-外斯定律：先求解上述方程组的解： 磁化率为： 或者表示为： 其中：

表格总结

磁性类型 磁化率行为 临界温度 备注
顺磁性 遵循居里定律 $\chi=\dfrac{C}{T}$ 无 高温下的普遍行为
铁磁性 遵循居里-外斯定律 $\chi=\dfrac{C}{T-T_C}$ $T_C=C\gamma,\quad \theta\approx T_C$ 存在自发磁化
反铁磁性 遵循奈耳定律 $\chi=\dfrac{C}{T+\theta}$ $T_N=C(\beta -\alpha),\quad \theta=C(\beta +\alpha)$ 磁矩反平行
亚铁磁性 遵循修正的居里-外斯定律 $\dfrac1\chi= \frac{T}{C}+ \frac{\rho}{T- \theta}+\frac{1}{\chi_0}$ $T_c = C\gamma\dfrac{(a\lambda +b\mu)+\sqrt{(a\lambda -b\mu)^2+4\lambda\mu}}{2}$
$\theta=C\gamma\lambda\mu(a+b+2)$		 子格磁矩不完全反平行

自旋相关输运

电子是电荷的载体，同时也是自旋的载体。至今为止，我们讨论电子的输运问题的时候，都只考虑电荷的输运，而忽略了自旋的输运。此时，我们认为电子是非自旋极化的，即自旋向上和自旋向下的电子数目相等。近些年发展的磁性材料让我们意识到，由于磁性金属是自旋极化的，电子的自旋输运会对整体的输运性质产生重要影响。自旋相关输运是自旋电子学的基础内容之一。

电子自旋隧穿电导与MRAM

电子隧穿电导

考虑一个金属隧道结，即两个金属电极中间被很薄的绝缘层分开的三明治结构：

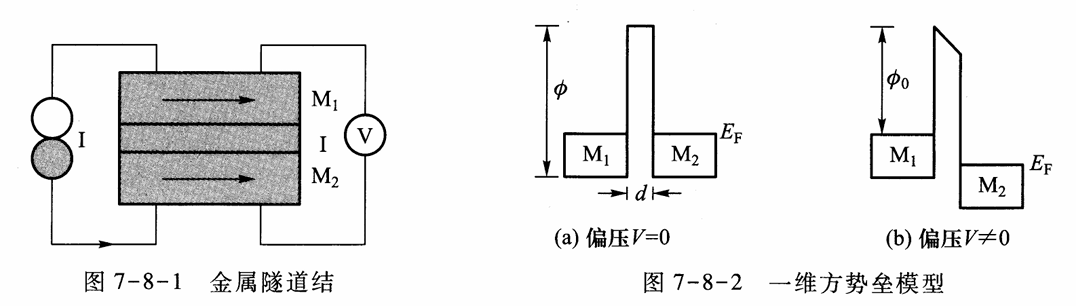
image.png

在 一维定态问题 中，我们曾解出有限高方势垒的隧穿概率：

考虑厚势垒$k_2d\gg 1$的情况，有$\sinh^2{k_2d}\approx \frac{1}{4}e^{2k_2d}$：

代入$k_1^2=\dfrac{2mE}{\hbar^2},\quad k_2^2=\dfrac{2m(\phi-E)}{\hbar^2}$，得到：

此时如果不加偏压，两个点击的费米面相等，电子从M1隧穿到M2的概率和从M2隧穿到M1的概率相等，净电流为0。

如果加上一个偏压$V$，则电子在两侧的能量分别为$E$和$E-eV$，此时可以直接写出隧穿电流的积分表达式：

在低偏压条件$eV \ll E_F$下，费米分布函数的差分近似为：

显然，在低偏压条件下，隧穿电流与偏压成正比，符合欧姆定律。

电子自旋隧穿电导

对于磁性金属电极，由于自旋向上和自旋向下的电子数目不相等，隧穿电流也会受到自旋极化的影响。我们定义自旋极化为：

在低偏压下，由无自旋电子隧穿电导的计算方法，我们可以得到自旋极化金属隧道结的隧穿电导，根据磁性金属的磁化方向分为平行磁化和反平行磁化：

进而定义电阻：

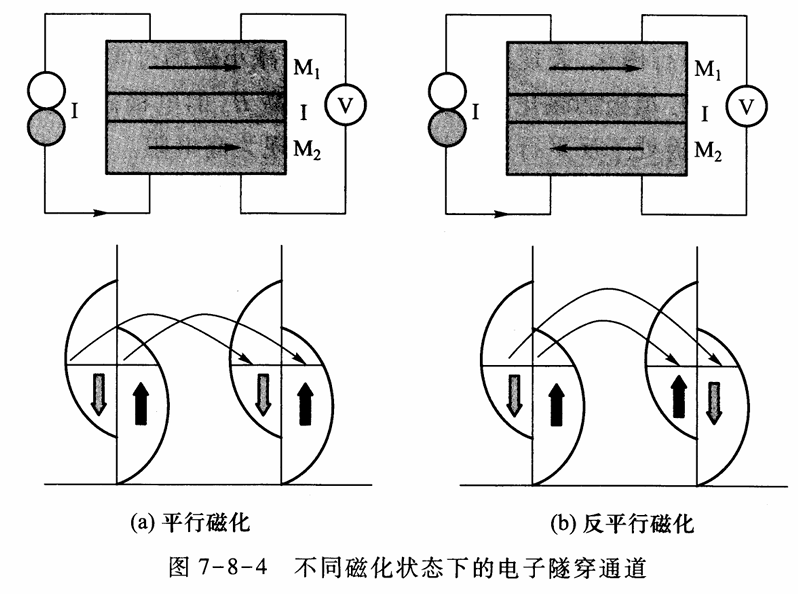
image.png

通过示意图可以很直观的了解到，反磁化平行的电阻$R_A$要大于平行的电阻$R_P$，这是因为反磁化平行（以图中为例）自旋向下的电子在M1中占多数，但在M2中只有少数空态能让其占据，所以隧穿的电子更少。

磁性隧道结这种依赖磁化状态的电阻变化称为隧道磁电阻（Tunneling Magnetoresistance, TMR）：

自旋阀结构

利用磁性隧道结的磁电阻依赖磁电机的磁化状态这一性质，可以设计出电阻对外场敏感的自旋阀结构（Spin Valve），用于磁存储器件中。最简单的自旋阀是由两种矫顽力不同（$H_1<H_2$）的磁电极构成的，由于矫顽力不同，当外场$H_1<H<H_2$时，产生的反平行磁化大于通常的平行磁化电阻，进而表现为电阻的突变。这种性能是随机存储器件MRAM（Magnetoresistive Random Access Memory）的基础。

实际应用中，通常会在矫顽力较大的部分下沉积一层反铁磁层，来固定其磁化方向，从而提高自旋阀的稳定性。

自旋流的产生