Content
Contend本博客的所有专栏的目录文章如下:
HexoHexo的安装与配置
本博客由Hexo搭建,使用了Github Pages进行托管。出于个人备份和分享的缘故,整理了搭建Hexo的过程和一些心得。
数学群论群论Content
为了满足科研的需要,我整理了群论的笔记。学习群论对量子力学和固体物理的理解是有裨益的。
主要的参考书籍为:李征新《群论及其在凝聚态物理中的应用》
物理学物理本科的时候延续了高中喜欢做笔记的习惯。从纸质笔记到平板电子笔记和Latex笔记,最终转向Markdown格式的电子笔记。上课的时候整理出以下笔记,并在夏令营复习期间进行了完善。
数学物理方法数学物理方法Content
对应的课程为PHY2501数学物理方程、PHY2508复变函数和PHY2510概率与统计。主要参考的书籍为:
《数学物理方法》梁昆淼;
《数学物理方程讲义》刘世勇;
理论力学理论力学Content
对应的课程为PHY1621力学与PHY2601分析力学。主要参考的书籍为:
《力学》舒幼生(老先生千古);
《力学》秦允豪;
《理论力学》梁昆淼;
高显、陈童、刘川等老师的讲义也有所借鉴。
...
磁性的来源
磁性概论
孤立原子的磁矩
无外场情况
原子磁矩对外场的响应
抗磁性
顺磁性
轨道猝灭效应
固体的磁性
泡利顺磁性
朗道抗磁性
铁磁性
外斯分子场理论
磁滞回线与磁晶的各向异性
Heisenberg模型
Stoner模型
铁磁自旋波
反铁磁性
双子格模型
奈耳定律
反铁磁自旋波
亚铁磁性
尖晶石结构
表格总结
自旋相关输运
电子自旋隧穿电导与MRAM
电子隧穿电导
电子自旋隧穿电导
自旋阀结构
自旋流的产生
磁性概论磁性本质上是一种量子效应,而固体的磁性又是大量孤立原子的磁性的集体效应。按照量子力学的理论,原子的磁矩主要来源于:
电子固有的自旋磁矩;
电子绕核运动产生的轨道磁矩;
外加磁场感生的轨道磁矩变化。
在经典图像中,前两个磁矩会跟随外场的方向,给出顺磁性的贡献,此时磁化率的大小大概在$0\sim 10^{-2}$之间,随温度的升高而降低,即居里定律:
\chi=\frac{C}{T}顺磁性的计算在 玻尔兹曼统计 中也曾提到过。
如果前两个磁矩耦合后为零,那么抗磁性作为二阶效应就会显现出来,这是因为磁场给电子提供额外的离心力,致使磁矩变小,磁 ...
总结
隔壁的2026夏令营/推免交流帖已经成为电院交流帖了,所以我打算新开个楼来分享一下个人的经历和经验,希望老东西们也能给小朋友们撑撑伞。考虑到我想说的东西不仅限于推免这块,而且小朋友现在也不至于就想着推免怎么搞,题目还是叫做
写在前面lz刚刚结束清华的预推免,突然空出了很多时间。复习的时候总归会回忆一些往事,然后就会有写东西的冲动。加上lz一直有在毕业前写一篇总结的计划,于是这篇经验帖应运而生。(其实很早就写完了,但是忙着打粥洲)
为了保护个人隐私,在谈到本科教育和保研经历的时候,不会涉及到具体的同学,不过应该能大概透露一下今年的去向:物院和致远都有去清北的同学,致远去清北的大于等于一手之数,物院应该也差不多(这应该是能说的?)。
今年是清华夏令营不发offer的第一年(影响比想象中的大,难道传说的鸽子链真的存在?),所以这篇帖子后面关于保研部分仅供参考,也会谈谈这次改革的具体影响。
写之前我本来只打算介绍一下保研的一些趣事,但写着写着就涉及到了物院和致远物理、新生必备的几个网站、以及大家一直都在争(水)论(楼)的致远物理要不要进的问题。严肃叠甲:错漏在所难免,欢迎大家补充。
在部分涉及 ...
WKB-Approximation
WKB Approximation
From Schrödinger Equation
From hbar expansion
Tunneling
Connection Formulas in Crossing Area
Sommerfeld Quantum Condition
Example
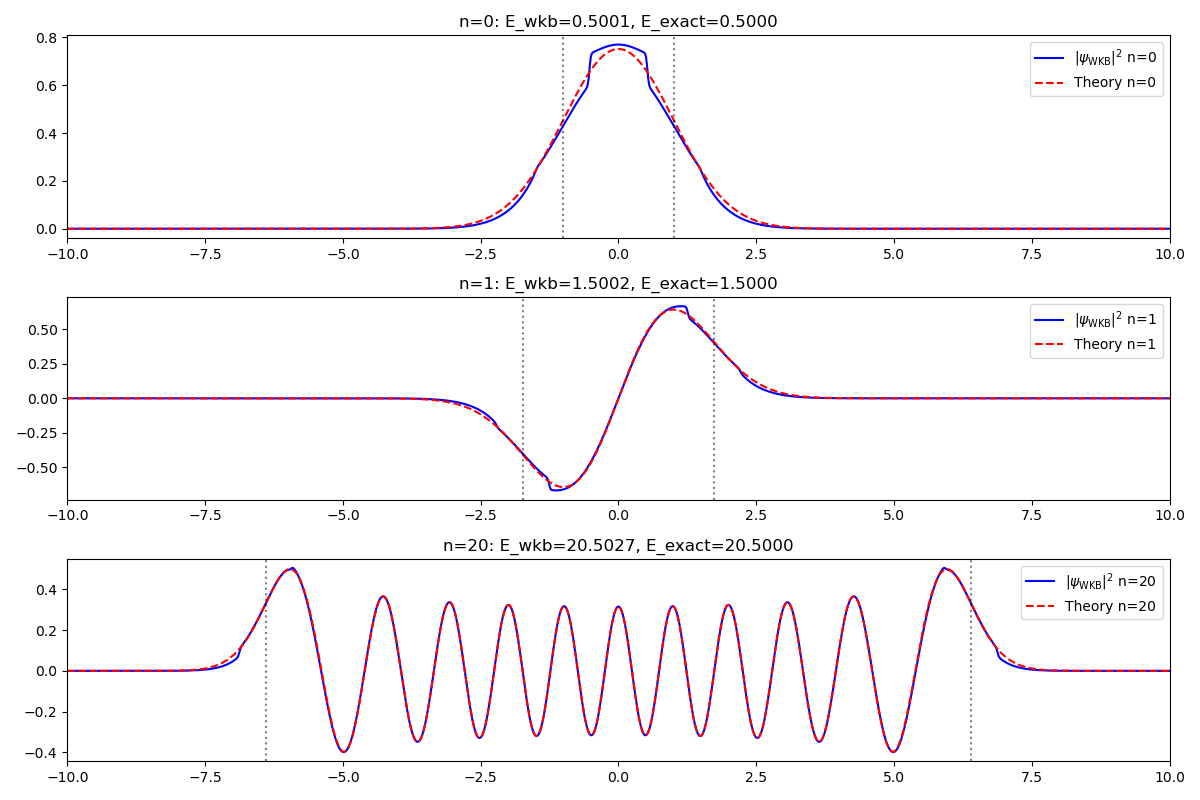
WKB近似是由Wentzel, Kramers和Brillouin三位科学家提出的,用于求解量子力学中的一维定态薛定谔方程(对于三维薛定谔方程的径向部分也是有帮助的)近似解的技术。其基本思想是,如果势能是一个常数,那么波函数可以写为正弦波动形式:
\psi(x)=Ae^{ikx}+Be^{-ikx},\quad k=\sqrt{\frac{2m(E-V)}{\hbar^2}}事实上,只要是势能变化不剧烈的部分,WKB近似就可以很好地应用。
如何衡量势能的变化程度呢?可以与波长$\lambda=\frac{2\pi}{k}$进行比较。当势能的变化范围远小于波长时,WKB近似是有效的。
对于能量小于势能的解,有类似的形式:
\psi(x)=Ce^{-\kappa x}+De^{\kappa ...
Time-Dependent-Perturbation
Time-dependent Problem
Interaction Picture
Example: Nuclear Magnetic Resonance
Time-dependet Perturbation
Dyson Series
Transition Probability
Constant Perturbation
Zero Order
First Order
Second Order
Harmonic Perturbation
Expotential Decay Perturbation-Energy Shift and Decay Width
First Order
Second Order
Lamb Shift
Time-dependent Problem从一阶微扰可以知道:
|n^1\rangle=\sum_k c_k|k\rangle随时间的演化:
|n^1(t)\rangle=\sum_k c_ke^{-\frac{iE_kt}{\hbar}}|k\rangle当我们考虑和哈密顿量和时间相关的时候
|n^1(t)\rangle=\sum_k c ...
Density-Matrix
密度矩阵的动机和历史
量子统计
复合系统
混合态和密度矩阵
纯态和混合态
从纯态引入密度算符
密度算符之于混合态
密度算符的运动方程
复合系统和约化密度矩阵
Schmidt分解定理
量子熵和极大熵原理
微正则系综
正则系综
巨正则系综
密度矩阵的动机和历史量子统计密度矩阵的概念起源于量子统计力学和量子测量理论,最早是由约翰·冯·诺伊曼在1927年提出的。当我们提到统计的时候,第一反应应该是量子力学中的系综是什么?系综是由许多不同的系统组成的,一个纯态$|\psi_j\rangle$可以类比为一个系统,而一堆纯态$\{|\psi_j\rangle:p_j\}$可以类比为一个系综。为了实现对系综的方便测量,比如测量其中$|m\rangle$态的比例/概率:
p(|m\rangle)=\sum_j p_j\langle \psi_j|\hat P_m|\psi_j\rangle其中$\hat P_m=|m\rangle\langle m|$是投影算符,$p_j$是系综中第$j$个纯态的概率。稍加化简,可以得到:
\begin{aligned}
p(|m\rangle)&=\s ...
量子力学的诞生
经典物理学的困境
黑体辐射
光电效应
原子结构
固体比热
量子力学的诞生
准备工作
量子力学的建立
量子力学公设和正则量子化
量子力学的五大公设
正则量子化
经典物理学的困境所有的所有都得从大家熟知的开尔文勋爵的那句名言开始:
经典物理学上空悬浮着两朵乌云:
电动力学中的电磁场如果依托于以太,为什么以太不被观测到?为什么天体可以无摩擦地穿行以太之中?
为什么物体的比热总是低于经典统计物理学的能均分定理给出的参考值?
第一个问题的回答是:电磁场本身就是物质的存在形式,以太是不存在的。回答第二个问题需要用到量子统计物理学——在低温时,部分自由度被冻结,在本质上涉及能量的量子化。
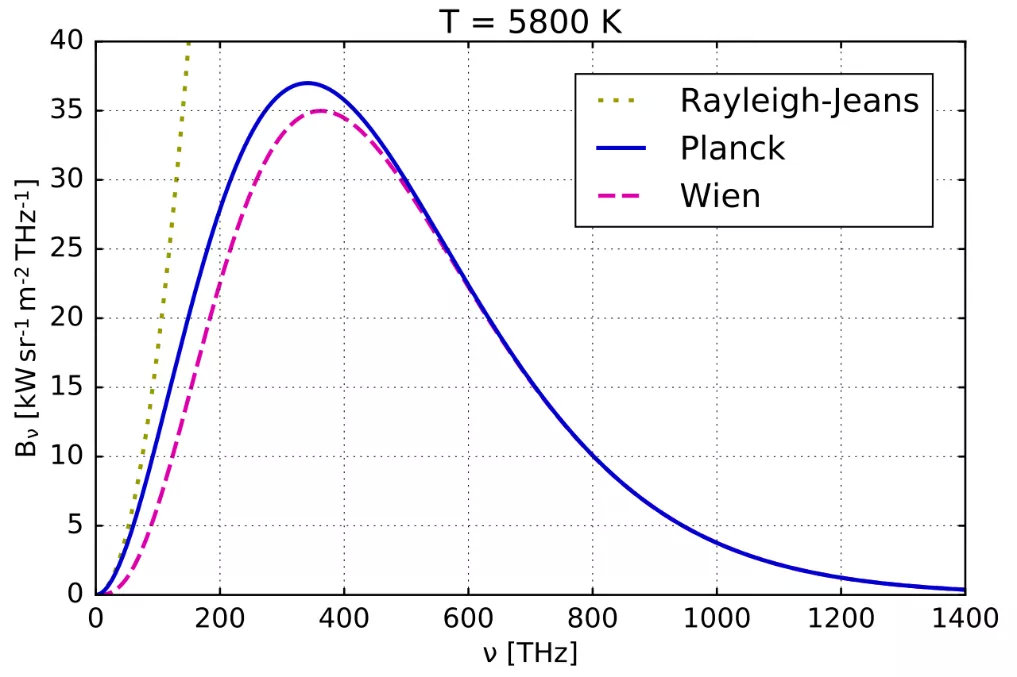
黑体辐射对热辐射的描述经历了很长一段时间,主要的成果有:
瑞利-金斯公式:$I(\nu,T)=\dfrac{8\pi kT \nu^2}{c^3}kT$,在长波段符合,却会导致紫外灾难。
维恩公式:$I(\nu,T)=\dfrac{8\pi h\nu^3}{c^3}\dfrac{1}{e^{h\nu/kT}}$,在短波段符合,但在长波段不符合。
普朗克公式:$I(\nu,T)=\dfrac ...