• WKB Approximation
  • From Schrödinger Equation
  • From hbar expansion
  • Tunneling
  • Connection Formulas in Crossing Area
  • Sommerfeld Quantum Condition
  • Example

WKB近似是由Wentzel, Kramers和Brillouin三位科学家提出的，用于求解量子力学中的一维定态薛定谔方程（对于三维薛定谔方程的径向部分也是有帮助的）近似解的技术。其基本思想是，如果势能是一个常数，那么波函数可以写为正弦波动形式：

$$\psi(x)=Ae^{ikx}+Be^{-ikx},\quad k=\sqrt{\frac{2m(E-V)}{\hbar^2}}$$

事实上，只要是势能变化不剧烈的部分，WKB近似就可以很好地应用。

如何衡量势能的变化程度呢？可以与波长$\lambda=\frac{2\pi}{k}$进行比较。当势能的变化范围远小于波长时，WKB近似是有效的。

对于能量小于势能的解，有类似的形式：

$$\psi(x)=Ce^{-\kappa x}+De^{\kappa x},\quad \kappa=\sqrt{\frac{2m(V-E)}{\hbar^2}}$$

现在只有一个地方让WKB近似不能很好地适用，那就是经典转折点附近，即$V(x)=E$的地方。此时，波长$\lambda$变为无穷大，WKB近似失效。在这个区域可以使用线性势近似处理。

WKB Approximation

WKB近似公式有两种推导方式，这里都写上来。

From Schrödinger Equation

一般一个波函数可以用振幅函数和相位函数表示：

$$\psi(x)=A(x)e^{i\phi(x)}$$

对其求二阶导：

$$\frac{d^2\psi}{dx^2}=\left[A''(x)+2A'(x)i\phi'(x)+iA(x)\phi''(x)-A(x)\phi'(x)^2\right]e^{i\phi(x)}$$

将其代入薛定谔方程中：

$$\frac{d^2\psi}{dx^2}=-\frac{p^2}{\hbar^2}\psi,\quad p=\sqrt{2m[E-V(x)]}$$

可以得到关于实部和虚部两个方程：

$$\begin{cases} A''(x)-A(x)\phi'(x)^2=-\frac{p^2}{\hbar^2}A(x)\\ 2A'(x)i\phi'(x)+iA(x)\phi''(x)=0 \end{cases}$$

第二个方程稍加变形即可得到：

$$\left[A(x)\phi'(x)\right]'=0\Rightarrow A^2(x)\phi'(x)=C^2\Rightarrow A(x)=\frac{C}{\sqrt{\phi'(x)}}$$

第一个方程很难求解，所以一般假设振幅函数变化缓慢，即$A’’(x)$可以忽略，得到：

$$-A(x)\phi'(x)^2=-\frac{p^2}{\hbar^2}A(x)\Rightarrow \phi'(x)=\pm\frac{p}{\hbar}\Rightarrow \phi(x)=\pm\frac{1}{\hbar}\int pdx$$

合起来就是：

$$\boxed{\psi(x)=\frac{C}{\sqrt{p(x)}}e^{\pm\frac{i}{\hbar}\int pdx}}$$

对其就模方：

$$|\psi(x)|^2=\frac{C^2}{p(x)}$$

这说明粒子出现在$x$附近的概率与动量$p(x)$成反比。这和经典图像是一致的。

From hbar expansion

将波函数写为平面波的形式，不过幂部分是个复函数：

$$\psi(x)=e^{if(x)/\hbar}$$

代入薛定谔方程：

$$\frac{d^2\psi}{dx^2}=-\frac{p^2}{\hbar^2}\psi,\quad p=\sqrt{2m[E-V(x)]}$$

得到：

$$i\hbar f''-(f')^2+p^2=0$$

对$f(x)$按$\hbar$做级数展开：

$$f(x)=f_0(x)+\hbar f_1(x)+\hbar^2 f_2(x)+\cdots$$

将其代入方程中，得到：

$$[p^2-(f_0')^2]+\hbar(if_0''-2f_0'f_1')+\hbar^2\cdots=0$$

系数对应后，得到：

$$\begin{cases} f_0'=\pm p\\ f_1'=i\dfrac{f_0''}{2f_0'} \end{cases}$$

解得：

$$\begin{cases} f_0=\pm\int p\,dx\\ f_1=\dfrac{i}{2}\ln |p| \end{cases}$$

代入即可得到WKB近似公式：

$$\boxed{\psi(x)=\frac{C}{\sqrt{p(x)}}e^{\pm\frac{i}{\hbar}\int pdx}}$$

这一种方法用于分析WKB近似的条件是很有帮助的。要想$\hbar$级数展开是成立的，就必须要求：

$$\frac{|\hbar(if_0''-2f_0'f_1')|}{|p^2-(f_0')^2|} \ll 1$$

代入$f_0’=\pm p, f_1’=i\dfrac{f_0’’}{2f_0’}$：

$$\frac{|\hbar(if_0''-2f_0'f_1')|}{|p^2-(f_0')^2|}=\frac{|\hbar f_0''|}{|p^2|}=\frac{|\hbar p'|}{|p^2|}=\frac{|\hbar p'|}{|p^2|}=\frac{\hbar}{2\sqrt{2m|E-V|}}\frac{|V'|}{|E-V|}=\frac{\lambda}{4\pi}\frac{|V'|}{|E-V|}$$

这说明要满足WKB近似，一方面要求$V’$很小，另一方面要求$E-V$很大（这不仅要求远离过渡区域，还要求经典区域$E-V$不能很小，典型粒子是谐振子势中$n$较小的时候误差很大）。

Tunneling

对于$E<<V(x)$的情况，此时唯一的区别是$p(x)=\sqrt{2m(E-V)}$变为虚数，所以只需要给WKB近似加上绝对值就行（虚数拉出来与$\dfrac{i}{\hbar}$相乘，并舍去发散的情况）：

$$\boxed{\psi(x)=\frac{C}{\sqrt{|p(x)|}}e^{-\frac{1}{\hbar}\int |p|dx}}$$

这个式子对我们了解隧穿效应是有启发的，对于一段长L的势垒，粒子穿过势垒的概率与势垒的宽度和高度有关：

$$\frac{A_{out}}{A_{in}}=\exp\left(-\frac{1}{\hbar}\int_L |p|dx\right)$$

其中宽度L直接影响积分的区间大小，而势垒高度则影响动量$p(x)$的大小。

Connection Formulas in Crossing Area

对于势能曲线和能量平行线交叉的区域，以上WKB近似失效，不过我们可以用线性势来近似这里的势能变化：

$$V(x)=E+V'(0)x$$

只需要求解：

$$\frac{d^2\psi}{dx^2}=\frac{2mV'(0)}{\hbar^2}x\psi$$

一般变为：

$$\frac{d^2\psi}{dz^2}=z\psi,\quad z=\alpha x,\quad \alpha=\sqrt[3]{\frac{2mV'(0)}{\hbar^2}}$$

这个方程就是艾里方程，具体解见 特殊函数和方程 ，这里直接写出：

$$\psi(z)=C_1Ai(z)+C_2Bi(z)$$

其中$Ai(z)$和$Bi(z)$分别是艾里函数的第一类和第二类解。经过与WKB近似解的系数比较，可以得到：

$$\psi(x)=\begin{cases} \frac{1}{\sqrt{p(x)}}\sin\left[\frac1\hbar\int_{x'}^0 pdx'+\frac\pi4\right],& x<x_0\\ \frac{1}{2\sqrt{|p(x)|}}\exp\left[\frac1\hbar\int_0^{x'} |p|dx'\right],& x>x_0 \end{cases}$$

这是对于$x<0,V<<E$的情况。另一种情况也是相似的。

Sommerfeld Quantum Condition

对于两个相近的经典转折点$a$和$b$，波函数必须同时满足：

$$C_1\frac{1}{\sqrt{p(x)}}\sin\left[\frac1\hbar\int_a^{x'} pdx'+\frac\pi4\right]=C_2\frac{1}{\sqrt{p(x)}}\sin\left[\frac1\hbar\int_{x'}^b pdx'+\frac\pi4\right]$$

记$\theta=\dfrac1\hbar\int_a^{x’} pdx’+\dfrac\pi4,\quad \sigma=\dfrac1\hbar\int_a^{b} pdx’+\dfrac\pi2$，则有：

$$C_1\sin\theta=C_2\sin(\sigma-\theta)$$

要使上恒成立，必须要有：

$$C_1=C_2, \sigma=2n\pi\quad \text{or} \quad C_1=-C_2, \sigma=(2n+1)\pi$$

合起来的条件是：

$$\sigma=n\pi,\quad \dfrac1\hbar\int_a^{b} pdx'+\dfrac\pi2=n\pi\Rightarrow \dfrac1{2\pi\hbar}\oint pdx'=n+\frac12$$

这是著名的索末菲量子化条件。将其用在谐振子势中，可以得到：

$$\int_a^b pdx=\pi\hbar\left(n+\frac12\right)$$

其中$a=-\frac{\sqrt{2E_n}}{\omega}, b=\frac{\sqrt{2E_n}}{\omega},p=\sqrt{2m(E-\frac12\omega^2x^2)}$。代入得到：

$$\int_{-\frac{\sqrt{2E_n}}{\omega}}^{\frac{\sqrt{2E_n}}{\omega}} \sqrt{2m\left(E-\frac12\omega^2x^2\right)}dx=\pi\hbar\left(n+\frac12\right)$$

这是一个标准的圆面积积分，容易解得：

$$E_n=\hbar\omega\left(n+\frac12\right)$$

Example

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import brentq
from scipy.special import airy, hermite, factorial

def Xi(x):
    return 1.0 / (1.0 + np.exp(-20 * (x - 0.5)))

def potential(x):
    return 0.5 * x ** 2

def ho_energy(n):
    return n + 0.5

def ho_psi(n, x):
    coeff = 1.0 / np.sqrt(2 ** n * factorial(n)) * (1/np.pi) ** 0.25
    Hn = hermite(n)
    return coeff * np.exp(-x ** 2 / 2) * Hn(x)

def sol_fun(fun, x_min, x_max, step):
    i = np.arange(x_min, x_max + step, step)
    root_E = []
    for ii in range(len(i) - 1):
        if fun(i[ii]) * fun(i[ii+1]) < 0:
            try:
                r = brentq(fun, i[ii], i[ii+1])
                root_E.append(r)
            except:
                pass
    return np.array(root_E)

def sol_ab(fun, x_min, x_max, step, E_n):
    y = lambda x: fun(x) - E_n
    root = sol_fun(y, x_min, x_max, step)
    if len(root) == 0:
        return np.array([[-np.inf, np.inf]]), np.array([[-np.inf, np.inf]])
    d_root = np.zeros_like(root)
    eps = 1e-6
    for i in range(len(root)):
        d_root[i] = (y(root[i]+eps) - y(root[i]-eps)) / (2*eps)
    ab = []
    ab_not = []
    for ii in range(len(d_root)):
        if d_root[ii] < 0:
            if ii != len(d_root)-1 and ii != 0:
                a, b = root[ii], root[ii+1]
                ab.append([a, b])
                ab_not.append([root[ii-1], root[ii]])
            elif ii == len(d_root)-1:
                a, b = root[ii], np.inf
                ab.append([a, b])
                ab_not.append([root[ii-1], root[ii]])
            elif ii == 0:
                a, b = root[ii], root[ii+1]
                ab.append([a, b])
                ab_not.append([-np.inf, root[ii]])
        else:
            if ii == 0:
                a, b = -np.inf, root[ii]
                ab.append([a, b])
            elif ii == len(d_root)-1:
                ab_not.append([root[ii], np.inf])
    return np.array(ab), np.array(ab_not)

def sol_energy(fun, xs, n, E_0):
    E_n = n + 0.5
    x_min, x_max = np.min(xs), np.max(xs)
    step = 10 * (xs[1] - xs[0])
    delta = 5
    ab, _ = sol_ab(fun, x_min, x_max, step, E_0)
    if ab[0,0] < -1e5 or ab[-1,1] > 1e5:
        return E_0
    def p(x, En):
        return np.sqrt(2 * np.abs(En - fun(x))) / np.pi
    end_ab = []
    for a_b in ab:
        xx = np.linspace(a_b[0], a_b[1], 400)
        end_ab.append(np.trapz(p(xx, E_0), xx) - E_n)
    while np.max(end_ab) < 0:
        E_0 = E_0 + delta
        ab, _ = sol_ab(fun, x_min, x_max, step, E_0)
        end_ab = []
        for a_b in ab:
            xx = np.linspace(a_b[0], a_b[1], 400)
            end_ab.append(np.trapz(p(xx, E_0), xx) - E_n)
    E_a = E_0 - delta
    E_b = E_0
    for i in range(20):
        E_mid = (E_a + E_b) / 2
        ab, _ = sol_ab(fun, x_min, x_max, step, E_mid)
        end_ab = []
        for a_b in ab:
            xx = np.linspace(a_b[0], a_b[1], 400)
            end_ab.append(np.trapz(p(xx, E_mid), xx) - E_n)
        if np.max(end_ab) < 0:
            E_a = (E_a + E_b) / 2
        else:
            E_b = (E_a + E_b) / 2
    return E_b

class WKB:
    def __init__(self, potential, xx, n, E_0):
        self.potential_sys = potential
        self.coordinate = xx
        self.potential = potential(xx)
        self.energy_leval = n
        self.energy = sol_energy(potential, xx, n, E_0)
        x_min, x_max = np.min(xx), np.max(xx)
        step = xx[1] - xx[0]
        self.root_E, self.ab_not = sol_ab(potential, x_min, x_max, step, self.energy)

    def WKB_psi_allow(self, x, a, b):
        p = lambda xx: np.sqrt(2 * np.abs(self.energy - self.potential_sys(xx)))
        int_p = np.zeros_like(x)
        psi = np.zeros_like(x)
        if a > -1e5:
            for i in range(len(x)):
                xx_ = np.linspace(a, x[i], 200)
                int_p[i] = np.trapz(p(xx_), xx_)
            psi = 1.0 / np.sqrt(p(x)) * np.cos(int_p - np.pi/4)
        else:
            for i in range(len(x)):
                xx_ = np.linspace(b, x[i], 200)
                int_p[i] = np.trapz(p(xx_), xx_)
            psi = 1.0 / np.sqrt(p(x)) * np.cos(int_p + np.pi/4)
        return psi

    def WKB_psi_forbidden(self, x):
        a = self.ab_not[np.where(self.ab_not[:,0] <= x[0])[0][-1], 0] if np.any(self.ab_not[:,0] <= x[0]) else -np.inf
        b = self.ab_not[np.where(self.ab_not[:,1] >= x[-1])[0][0], 1] if np.any(self.ab_not[:,1] >= x[-1]) else np.inf
        p = lambda xx: np.sqrt(2 * np.abs(self.energy - self.potential_sys(xx)))
        int_pa = np.zeros_like(x)
        int_pb = np.zeros_like(x)
        psi = np.zeros_like(x)
        if a < -1e5:
            for i in range(len(x)):
                xx_ = np.linspace(x[i], b, 200)
                int_pb[i] = np.trapz(p(xx_), xx_)
            psi = 1.0 / (2 * p(x)) * np.exp(-int_pb)
        elif b > 1e5:
            for i in range(len(x)):
                xx_ = np.linspace(a, x[i], 200)
                int_pa[i] = np.trapz(p(xx_), xx_)
            psi = 1.0 / (2 * p(x)) * np.exp(-int_pa)
        else:
            for i in range(len(x)):
                xx1 = np.linspace(a, x[i], 200)
                xx2 = np.linspace(x[i], b, 200)
                int_pa[i] = np.trapz(p(xx1), xx1)
                int_pb[i] = np.trapz(p(xx2), xx2)
            psi = 1.0/(2*p(x))*np.exp(-int_pa) + 1.0/(2*p(x))*(np.exp(-int_pb)-np.exp(-int_pa))*Xi((x-a)/(b-a))
        return psi

    def WKB_airy(self, x, F, ab):
        F = float(F)
        pref = np.sqrt(np.pi) / (2 * np.abs(F))**(1/6)
        if F < 0:
            F = -F
            arg = (2*F)**(1/3) * (ab - x)
        else:
            arg = (2*F)**(1/3) * (x - ab)
        return pref * airy(arg)[0]

    def approx_psi(self, delta, delta_tran):
        x = self.coordinate
        ab = self.root_E
        size_ab = ab.shape
        psi = np.zeros_like(x)
        for num_ab in range(size_ab[0]):
            a, b = ab[num_ab,0], ab[num_ab,1]
            # 数值微分
            F_a = (self.potential_sys(a + 1e-4) - self.potential_sys(a - 1e-4)) / 2e-4
            F_b = (self.potential_sys(b + 1e-4) - self.potential_sys(b - 1e-4)) / 2e-4
            # allowed
            i_a = np.argmax(x > a + delta + delta_tran)
            i_b = len(x) - np.argmax(x[::-1] < b - delta - delta_tran) - 1
            psi[i_a:i_b+1] = self.WKB_psi_allow(x[i_a:i_b+1], a, b)
            # airy a
            if a > -1e5:
                i_a = np.argmax(x > a - delta)
                i_b = len(x) - np.argmax(x[::-1] < a + delta) - 1
                psi[i_a:i_b+1] = self.WKB_airy(x[i_a:i_b+1], F_a, a)
            # airy b
            if b < 1e5:
                i_a = np.argmax(x > b - delta)
                i_b = len(x) - np.argmax(x[::-1] < b + delta) - 1
                psi[i_a:i_b+1] = ((-1)**self.energy_leval) * self.WKB_airy(x[i_a:i_b+1], F_b, b)
            # 拼接
            if a >= -1e5:
                i_a1 = np.argmax(x > a + delta)
                i_b1 = len(x) - np.argmax(x[::-1] < a + delta + delta_tran) - 1
                i_a2 = np.argmax(x > a - delta - delta_tran)
                i_b2 = len(x) - np.argmax(x[::-1] < a - delta) - 1
                xx1 = x[i_a1:i_b1+1]
                xx2 = x[i_a2:i_b2+1]
                if F_a > 0:
                    psi[i_a1:i_b1+1] = self.WKB_airy(xx1, F_a, a) + (self.WKB_psi_forbidden(xx1) - self.WKB_airy(xx1, F_a, a))*Xi((xx1-a-delta)/delta_tran)
                    psi[i_a2:i_b2+1] = self.WKB_psi_allow(xx2, a, b) + (self.WKB_airy(xx2, F_a, a) - self.WKB_psi_allow(xx2, a, b))*Xi((xx2-a+delta+delta_tran)/delta_tran)
                else:
                    psi[i_a1:i_b1+1] = self.WKB_airy(xx1, F_a, a) + (self.WKB_psi_allow(xx1, a, b) - self.WKB_airy(xx1, F_a, a))*Xi((xx1-a-delta)/delta_tran)
                    psi[i_a2:i_b2+1] = self.WKB_psi_forbidden(xx2) + (self.WKB_airy(xx2, F_a, a) - self.WKB_psi_forbidden(xx2))*Xi((xx2-a+delta+delta_tran)/delta_tran)
            if b <= 1e5:
                i_a1 = np.argmax(x > b + delta)
                i_b1 = len(x) - np.argmax(x[::-1] < b + delta + delta_tran) - 1
                i_a2 = np.argmax(x > b - delta - delta_tran)
                i_b2 = len(x) - np.argmax(x[::-1] < b - delta) - 1
                xx1 = x[i_a1:i_b1+1]
                xx2 = x[i_a2:i_b2+1]
                if F_b > 0:
                    psi[i_a1:i_b1+1] = ((-1)**self.energy_leval)*(self.WKB_airy(xx1, F_b, b)+(self.WKB_psi_forbidden(xx1)-self.WKB_airy(xx1, F_b, b))*Xi((xx1-b-delta)/delta_tran))
                    psi[i_a2:i_b2+1] = self.WKB_psi_allow(xx2, a, b)+(((-1)**self.energy_leval)*self.WKB_airy(xx2, F_b, b)-self.WKB_psi_allow(xx2, a, b))*Xi((xx2-b+delta+delta_tran)/delta_tran)
                else:
                    psi[i_a1:i_b1+1] = ((-1)**self.energy_leval)*self.WKB_airy(xx1,F_b,b)+(self.WKB_psi_allow(xx1,a,b)-((-1)**self.energy_leval)*self.WKB_airy(xx1,F_b,b))*Xi((xx1-b-delta)/delta_tran)
                    psi[i_a2:i_b2+1] = ((-1)**self.energy_leval)*self.WKB_psi_forbidden(xx2)+(self.WKB_airy(xx2,F_b,b)-self.WKB_psi_forbidden(xx2))*Xi((xx2-b+delta+delta_tran)/delta_tran)
            # 禁止区多段
            num_a_before = np.where(self.ab_not[:,0] < a)[0]
            num_b_end = np.where(self.ab_not[:,1] > b)[0]
            if len(num_a_before) > 0:
                a_before = self.ab_not[num_a_before[-1],0]
                i_a = np.argmax(x > a_before + delta + delta_tran)
                i_b = len(x) - np.argmax(x[::-1] < a - delta - delta_tran) - 1
                psi[i_a:i_b+1] = self.WKB_psi_forbidden(x[i_a:i_b+1])
            if len(num_b_end) > 0:
                b_end = self.ab_not[num_b_end[0],1]
                i_a = np.argmax(x > b + delta + delta_tran)
                i_b = len(x) - np.argmax(x[::-1] < b_end - delta - delta_tran) - 1
                psi[i_a:i_b+1] = ((-1)**self.energy_leval)*self.WKB_psi_forbidden(x[i_a:i_b+1])
        norm = np.sqrt(np.sum((x[1]-x[0]) * psi**2))
        psi = psi / norm
        rho = psi
        return rho, norm

# 波函数模方、1/p对比
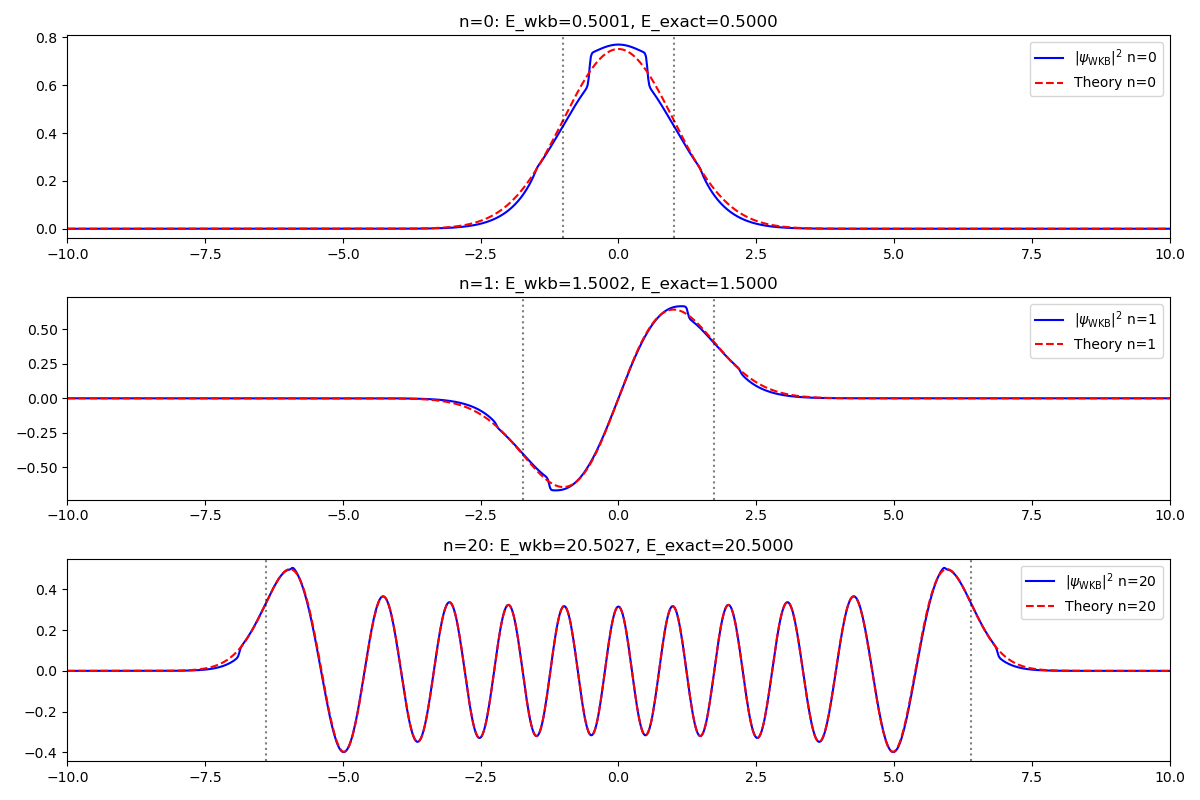
if __name__ == "__main__":
    N_list = [0, 1, 20]
    x_grid = np.linspace(-15, 15, 1201)
    delta = 0.35
    delta_tran = 0.25

    plt.figure(figsize=(12, 8))
    for idx, n in enumerate(N_list):
        wkb = WKB(potential, x_grid, n, ho_energy(n))
        psi_wkb, _ = wkb.approx_psi(delta, delta_tran)
        psi_th = ho_psi(n, x_grid)
        sign = np.sign(np.trapz(psi_wkb * psi_th, x_grid))
        psi_wkb *= sign
        norm_th = np.sqrt(np.trapz(psi_th ** 2, x_grid))
        psi_th /= norm_th
        plt.subplot(len(N_list), 1, idx+1)
        plt.plot(x_grid, psi_wkb, label=f'$|\\psi_{{\\rm WKB}}|^2$ n={n}', color='blue')
        plt.plot(x_grid, psi_th, '--', label=f'Theory n={n}', color='red')
        for ab in wkb.root_E:
            plt.axvline(ab[0], color='k', linestyle=':', alpha=0.5)
            if ab[1] < 1e5:
                plt.axvline(ab[1], color='k', linestyle=':', alpha=0.5)
        plt.title(f"n={n}: E_wkb={wkb.energy:.4f}, E_exact={ho_energy(n):.4f}")
        plt.legend()
        plt.xlim(-15, 15)
    plt.tight_layout()
    plt.show()

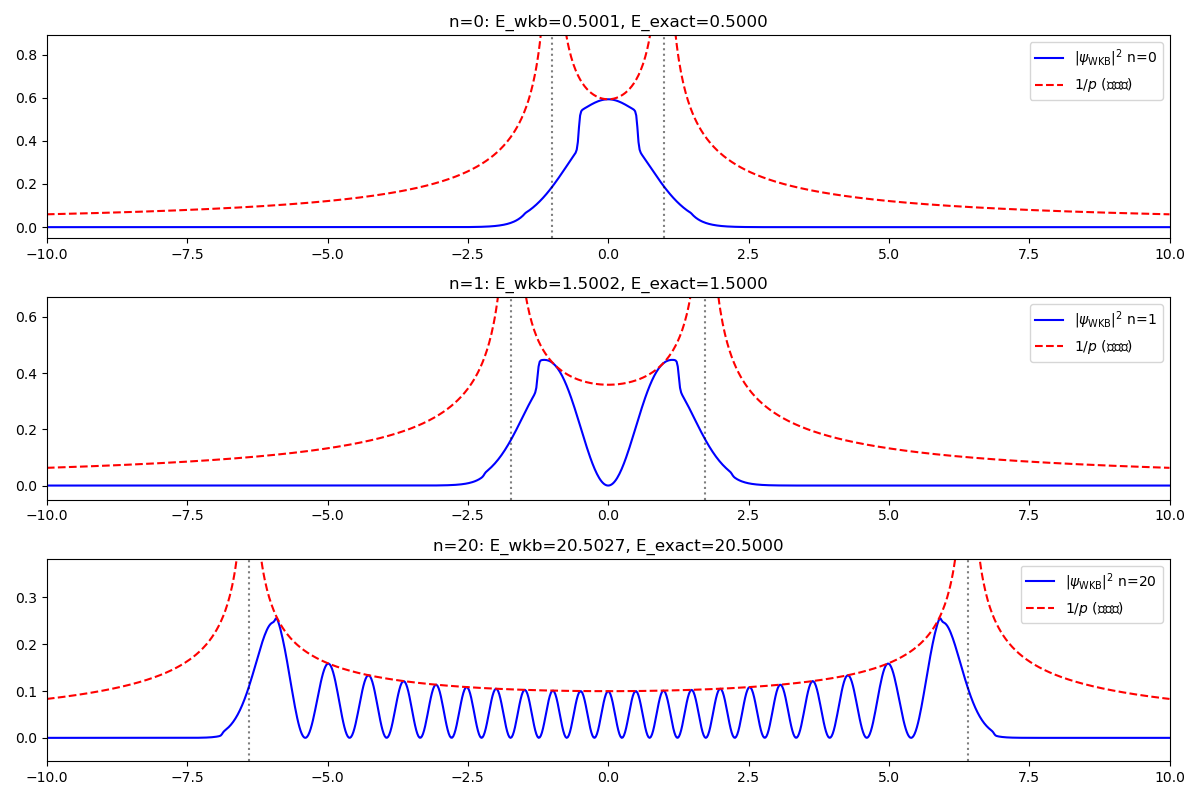
    plt.figure(figsize=(12, 8))
    for idx, n in enumerate(N_list):
        wkb = WKB(potential, x_grid, n, ho_energy(n))
        psi_wkb, norm = wkb.approx_psi(delta, delta_tran)
        psi_mod = psi_wkb**2
        # 1/p 曲线
        p = np.sqrt(2 * np.abs(wkb.energy - wkb.potential))
        # 避免除0
        p[p==0] = np.nan
        invp = 1/norm**2 / p
        plt.subplot(len(N_list), 1, idx+1)
        plt.plot(x_grid, psi_mod, label=f'$|\\psi_{{\\rm WKB}}|^2$ n={n}', color='blue')
        plt.plot(x_grid, invp, '--', label='$1/p$ (归一化)', color='red')
        for ab in wkb.root_E:
            plt.axvline(ab[0], color='k', linestyle=':', alpha=0.5)
            if ab[1] < 1e5:
                plt.axvline(ab[1], color='k', linestyle=':', alpha=0.5)
        plt.title(f"n={n}: E_wkb={wkb.energy:.4f}, E_exact={ho_energy(n):.4f}")
        plt.legend()
        plt.xlim(-15, 15)
        plt.ylim(-0.05, 1.1*np.max(psi_mod))
    plt.tight_layout()
    plt.show()