量子力学的诞生

• 经典物理学的困境
  • 黑体辐射
  • 光电效应
  • 原子结构
  • 固体比热
• 量子力学的诞生
  • 准备工作
  • 量子力学的建立
• 量子力学公设和正则量子化
  • 量子力学的五大公设
  • 正则量子化

经典物理学的困境

所有的所有都得从大家熟知的开尔文勋爵的那句名言开始：

经典物理学上空悬浮着两朵乌云：

• 电动力学中的电磁场如果依托于以太，为什么以太不被观测到？为什么天体可以无摩擦地穿行以太之中？
• 为什么物体的比热总是低于经典统计物理学的能均分定理给出的参考值？

第一个问题的回答是：电磁场本身就是物质的存在形式，以太是不存在的。回答第二个问题需要用到量子统计物理学——在低温时，部分自由度被冻结，在本质上涉及能量的量子化。

黑体辐射

对热辐射的描述经历了很长一段时间，主要的成果有：

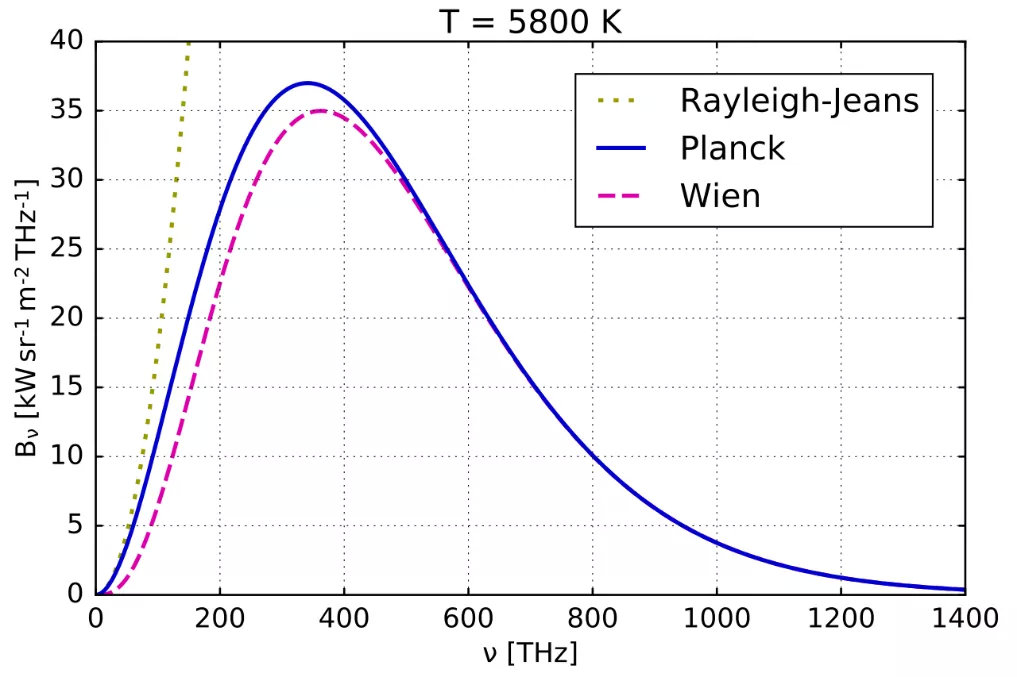
• 瑞利-金斯公式：$I(\nu,T)=\dfrac{8\pi kT \nu^2}{c^3}kT$，在长波段符合，却会导致紫外灾难。
• 维恩公式：$I(\nu,T)=\dfrac{8\pi h\nu^3}{c^3}\dfrac{1}{e^{h\nu/kT}}$，在短波段符合，但在长波段不符合。
• 普朗克公式：$I(\nu,T)=\dfrac{8\pi h\nu^3}{c^3}\dfrac{1}{e^{h\nu/kT}-1}$，在所有波段都符合。

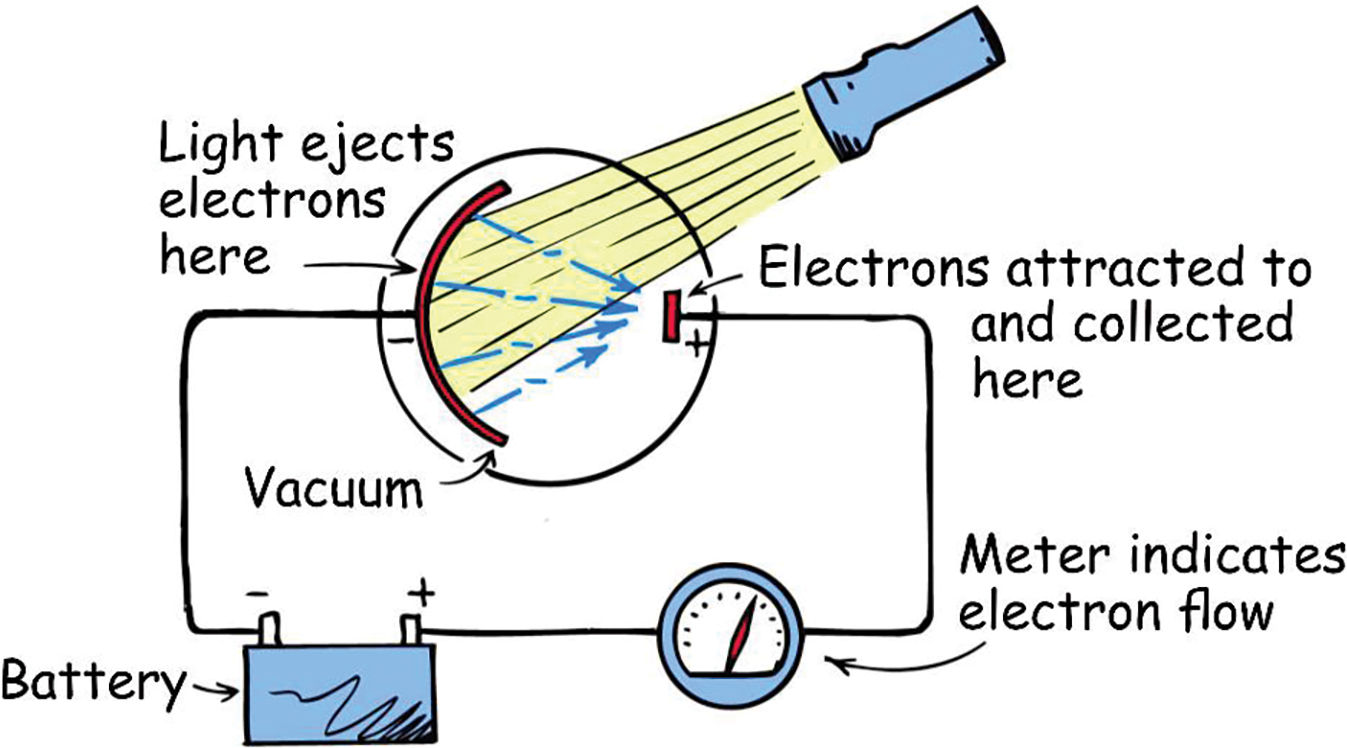
光电效应

光电效应是指光照射到金属表面时，金属表面会发射出电子。经典物理学认为光是波动现象，能量与振幅成正比，因此光的强度越大，电子的动能就越大。然而实验发现：

• 对于一定金属，有一个确定的截止频率$\nu_0$，只有当光的频率大于这个截止频率时，才会有电子被发射出来。（与强度无关）
• 每个光电子的能量只与光的频率有关，而与光的强度无关。
• 无论光多么微弱，只要光一照射到金属表面，就会立即（$\sim 10^{-9}s$）发射出电子。

定性上，经典物理学无法解释光的能量与强度无关，以及截止频率的存在；定量上，经典电磁理论计算的逸出时间远大于实验测得的时间。

原子结构

在 原子的结构 中提到了原子光谱的实验现象：原子在激发后会发射出特定频率的光：

$$\nu=R\left(\dfrac{1}{n_1^2}-\dfrac{1}{n_2^2}\right)$$

这些频率与原子的结构有关。经典物理学无法解释为什么原子只发射特定频率的光，而不是连续的光谱。同时，物理学家也无法解释原子的稳定性，即电子在运动过程中不会辐射能量而坠入原子核。

固体比热

在 玻尔兹曼统计 、 晶格动力学 和 金属电子论 中计算了声子的热容（爱因斯坦理论和德拜理论）和电子的热容。

按照经典理论，固体的比热应该是：

$$C_V=3R$$

然而实验发现，固体的比热在低温时远低于这个值（趋于零）。这其实是因为低温下，高能量的自由度被冻结，只有低能量的自由度参与热容的贡献。

量子力学的诞生

准备工作

在量子力学的诞生之前，物理学家们已经积累了大量的实验数据和理论成果。普朗克提出了光量子理论，解决了黑体辐射问题；爱因斯坦在光量子理论的基础上解释了光电效应；康普顿散射实验则进一步证实了光的量子性。

在光谱的启发下，玻尔提出了原子的量子模型，从而解释了原子光谱的现象。玻尔假设原子具有一系列能量不连续的定态，电子在定态上运动时不会辐射能量，而只有在跃迁到其他定态时才会发射或吸收光子。

我们在之后也会谈论波函数的定态问题。这里定态的意思都是一样的。

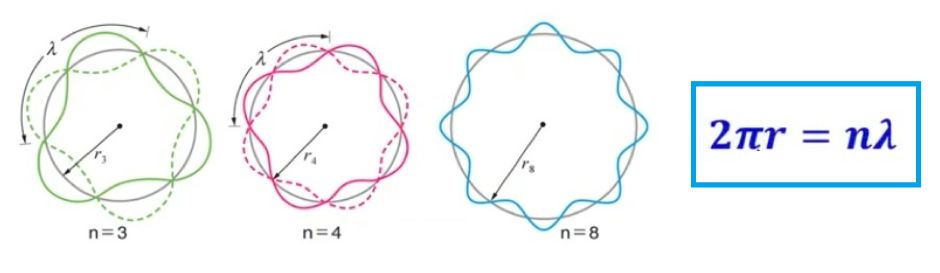
玻尔的定态假设毕竟牵强，德布罗意则把定态和物质波的驻波联系起来。在光的波粒二象性基础上，德布罗意认为实物粒子也具有波动性，提出了物质波的概念。德布罗意假设粒子的波长与其动量成反比：

$$\lambda = \frac{h}{p}$$

再联系驻波条件：

$$\lambda = \frac{2\pi r}{n}$$

自然得到了角动量量子化条件：

$$L = rp=\frac{rh}{\lambda}=\frac{nh}{2\pi}=n\hbar$$

物质波理论虽然简陋，但实物粒子的波动性却在之后被直接证明。1927年，戴维森和革末尔通过电子衍射实验直接证明了电子的波动性，验证了德布罗意的假设。

量子力学的建立

在 哈密顿力学 中曾提到，量子力学至少有三种等价表述：

分析力学	量子力学
泊松括号（刘维尔定理）	矩阵力学（海森堡方程）
哈密顿-雅可比方程	波动力学（薛定谔方程）
拉格朗日力学	路径积分

其中矩阵力学（1925）和波动力学（1926）几乎是同时提出的。对于矩阵力学，海森堡把每一个物理量对应一个矩阵，其代数运算规则遵循不可对易的代数，导出的海森堡方程形式上和刘维尔方程接近。在这个过程中，玻尔的对应原理起到了重要作用。

对于波动力学，薛定谔等人发展了德布罗意波的思想，提出了薛定谔方程。薛定谔还证明了矩阵力学和波动力学是等价的。

量子理论建立之后，玻恩提出了波函数的统计诠释，解决了量子力学的自洽性和物理意义问题。狄拉克在提出了相对论的量子力学，预言了正电子。玻色提出了玻色-爱因斯坦统计，爱因斯坦在此基础上提出了玻色-爱因斯坦凝聚，建立了量子统计物理学。泡利提出了泡利不相容原理，费米和狄拉克则发展了费米-狄拉克统计。

这些几乎都是在20世纪20年代完成的。在40年代，费曼提出了等价的路径积分表述，进一步丰富了量子力学的理论框架。

量子力学公设和正则量子化

本学期的学习中并不看重公理化体系的引入，不过这里还是简单的介绍一下，学完量子力学不免有的疑问在这里可以稍作解答。这里采用普遍认同的量子力学公设系统，并解释其中一次量子化和二次量子化的部分。

量子力学的五大公设

1. 波函数公设：

   • 波函数$\psi(\vec{r})$用于描述量子系统的状态。更数学地讲，希尔伯特空间中的矢量$\left|\psi\right\rangle$可以描述微观系统的状态，那么波函数是态矢量在某一表象下的投影
   • 关于波函数的物理意义，比较公认的是玻恩的统计诠释，即波函数的模方描述在空间中某点发现粒子的概率幅： $$dP(\vec{r})=|\psi(\vec{r})|^2d\vec{r}=\langle \psi|\vec{r}\rangle\langle \vec{r}|\psi\rangle d\vec{r}$$ 结合后面谈到的完备性基底，可以证明概率幅是归一化的： $$\int dP(\vec{r})=\int \langle \psi|\vec{r}\rangle\langle \vec{r}|\psi\rangle d\vec{r}=\langle \psi|\psi\rangle=1$$

   • 态叠加原理：如果$\psi_1$和$\psi_2$是两个可能的态，那么它们的线性组合也是一个可能的态，且系数服从统计诠释（正比于概率）：

     $$\text{discrete } |\psi\rangle=\sum_i\lvert a_i\rangle c_i , c_i=\langle a_i\rvert \psi\rangle ,P=c_i^*c_i$$ $$\text{continuous } |\psi\rangle=\int\lvert a\rangle \psi(a)da , \psi(a)=\langle a\rvert \psi\rangle ,P=\psi(a)^*\psi(a)$$

     态叠加原理意味着量子力学是一个线性的理论，具体而言，如果两个态的叠加是一个态，那么也应该满足薛定谔方程，即哈密顿算符应该是个线性算符。

2. 算符公设：希尔伯特空间中的厄密算符可以描述微观系统的物理量，而物理量的具体数值，取决于算符的本征值。至于为什么必须是厄密算符，是因为实验中的测量都是实数：

   $$\hat A|\psi\rangle = \lambda|\psi\rangle\Rightarrow \langle\psi|\hat A\psi\rangle=\langle\hat A^\dagger\psi|\psi\rangle = \lambda\langle\psi|\psi\rangle\Rightarrow \hat A^\dagger=\hat A$$
3. 测量公设：对物理量进行测量的时候，测量结果一定是本征值之一，且概率遵从态矢量的玻恩统计诠释（即态矢量中包含了“多少”该本征矢量）。测量结束后，态矢量坍缩为相应本征态矢量。测量的行为可以用投影算符描述： $$\hat P_a=|\psi_a\rangle\langle\psi_a|,\hat P_a |\psi\rangle=P_a|\psi_a\rangle$$ 其中$|\psi_a\rangle$是本征态矢量，$\hat P_a$是投影算符。测量后，态矢量变为： $$|\psi\rangle\rightarrow|\psi_a\rangle$$ 可以将厄米算符进行谱分解： $$\hat A=\sum_a a\hat P_a=\sum_a a|\psi_a\rangle\langle\psi_a|$$

4. 演化公设：波函数或态矢量的演化由薛定谔方程决定：

   $$\mathrm{i}\hbar\frac\partial{\partial t}|\psi(t)\rangle=H|\psi(t)\rangle$$

   定义时间演化算符：

   $$|\psi(t)\rangle=\hat{\Lambda}(t,t_0)|\psi(t_0)\rangle$$

   波函数的归一化要求$\hat{\Lambda}(t,t_0)$是幺正的，即：

   $$\langle\psi(t)|\psi(t)\rangle=1\Rightarrow\hat{\Lambda}(t,t_0)\hat{\Lambda}^\dagger(t,t_0)=1$$

   初值条件同时需要：

   $$\lim_{t\rightarrow 0}\hat{\Lambda}(t,t_0)=1$$

   转写为等价形式：

   $$\hat{\Lambda}(t,t_0)=e^{i\hat{\Omega}(t-t_0)}$$

   对演化后的态矢量求导：

   $$\frac{\partial}{\partial t}|\psi(t)\rangle=i\hat{\Omega}|\psi(t)\rangle$$

   这就有点薛定谔方程的雏形了，令$\hat{H}=-i\hbar\hat{\Omega}$，即可得到

   $$\mathrm{i}\hbar\frac\partial{\partial t}|\psi(t)\rangle=\hat{H}|\psi(t)\rangle$$

   这似乎预示着算符是比方程更根本的东西，我们同样可以定义空间算符，详见 对称性和守恒律 。

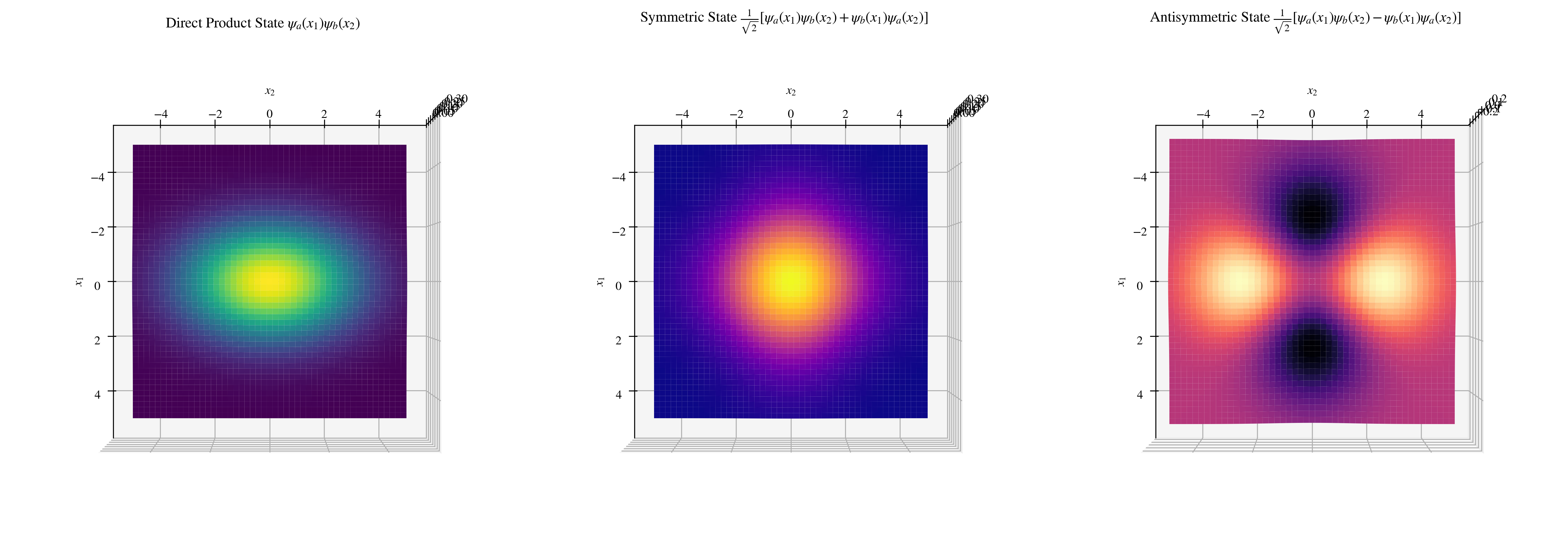
5. 全同性原理：全同粒子指的是内禀属性（质量、电荷、自旋等）完全相同的粒子。对于多粒子系统，出于全同粒子的不可分辨性，其概率幅随着粒子的交换而不变，也就是说波函数要么是对称的，要么是反对称的：

   $$\psi(x_1,x_2,\ldots,x_n)=\pm\psi(x_{\sigma(1)},x_{\sigma(2)},\ldots,x_{\sigma(n)})$$

   满足正号的波函数是玻色子（对称），满足负号的波函数是费米子（反对称）。

正则量子化

有的地方会把量子化条件纳入公设的范围，这里不作评价，仅讨论其中的逻辑。在历史上，狄拉克注意到了算符演化：

$$\frac{d}{dt}\langle \hat{O}\rangle=\frac{1}{i\hbar}\langle[\hat{O},\hat{H}]\rangle+\langle\frac{\partial \hat{O}}{\partial t}\rangle$$

和经典哈密顿力学中的物理量演化：

$$\frac{d}{dt}O=\{O,H\}+\frac{\partial O}{\partial t}$$

的相似关系，并提出通过建立对易子和泊松括号的桥梁——这正是正则量子化的思想。对于经典力学中的正则坐标和正则动量，其泊松括号和对易子分别为：

$$\{P_i,X_j\}=\delta_{ij},[P_i,X_j]=i\hbar\delta_{ij}$$

这中间只相差了一个系数$i\hbar$（事实上对于大部分物理量都是如此，但并非恒成立），这被称为一次量子化。相应地，上述量子化无法处理多粒子体系，因而需要新的量子化。对经典场论的量子化被称为二次量子化：

$$\text{boson } [\hat{a}_i,\hat{a}_j]=0,[\hat{a}_i^\dagger,\hat{a}_j^\dagger]=0, [\hat{a}_i,\hat{a}_j^\dagger]=\delta_{ij}$$ $$\text{fermion } \{\hat{c}_i,\hat{c}_j\}=0,\{\hat{c}_i^\dagger,\hat{c}_j^\dagger\}=0, \{\hat{c}_i,\hat{c}_j^\dagger\}=\delta_{ij}$$