转动群

SO(3)群的描述

在 刚体力学 中曾谈到了欧拉转动角表述。现在我们用同样的办法（但是不同的约定）来描述SO(3)群的元素：

$$\begin{aligned} \mathbf{R} &= \mathbf{R}_{z''}(\gamma) \mathbf{R}_{y'}(\beta) \mathbf{R}_{z}(\alpha) \\ &=\begin{pmatrix} \cos\alpha & -\sin\alpha & 0 \\ \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{pmatrix} \begin{pmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} \cos\alpha\cos\beta\cos\gamma-\sin\alpha\sin\gamma & -\cos\alpha\cos\beta\sin\gamma-\sin\alpha\cos\gamma & \cos\alpha\sin\beta \\ \sin\alpha\cos\beta\cos\gamma+\cos\alpha\sin\gamma & -\sin\alpha\cos\beta\sin\gamma+\cos\alpha\cos\gamma & \sin\alpha\sin\beta \\ -\sin\beta\cos\gamma & \sin\beta\sin\gamma & \cos\beta \end{pmatrix}\end{aligned}$$

这里的转动约定是：

• 先绕$z$轴转动$\alpha$角；
• 再绕$y’$轴转动$\beta$角；
• 最后绕$z’’$轴转动$\gamma$角。

SU(2)群的描述

考虑SU(2)群的酉表示：

$$\mathbf{U} =\begin{pmatrix} a & b \\ -b^* & a^* \end{pmatrix}$$

其中$a,b\in\mathbb{C}$，满足归一化条件：

$$|a|^2 + |b|^2 = 1$$

SO(3)和SU(2)的关系

直观理解

令$a=x_1+ix_2$，$b=x_3+ix_4$，则SU(2)的归一化条件等价于：

$$x_1^2 + x_2^2 + x_3^2 + x_4^2 = 1$$

这是一个四维球面方程，共有三个自由度。

而SO(3)的转动角$\alpha,\beta,\gamma$同样反映了三个自由度。这说明SO(3)和SU(2)之间存在一种对应关系（但并非一一对应，而是二重覆盖，我们后面会谈到）。现在我们用知乎·東雲正樹和知乎·高堡名人的回答来理解这一问题。

SO(3)群的元素对应了三维空间的转动，该转动可以用三维空间的矢量$\vec{\omega}$来描述，矢量的方向即是转动轴，大小即是转动角。SO(3)群的元素可以表示为三维空间中半径为$\pi$的球内的点。

但要注意的是，在球面上，由于$\vec{\omega}$和$-\vec{\omega}$表示同一个转动（顺时针转动$\pi$和逆时针转动$\pi$），因此SO(3)群的元素实际上对应于了一个开球$x_1^2+x_2^2+x_3^2<\pi^2$和半个球面$x_1^2+x_2^2+x_3^2=\pi^2,x_3>0$（专业称呼为对径认同）。

而SU(2)群的元素对应于四维空间中的单位球面$x_1^2+x_2^2+x_3^2+x_4^2=1$，这实际上是对应了两个SO(3)群的三维球：

$$\begin{cases} x_1^2+x_2^2+x_3^2<1,x_4>0 &\oplus&x_1^2+x_2^2+x_3^2=1,x_3>0,x_4=0\\ x_1^2+x_2^2+x_3^2<1,x_4<0 &\oplus&x_1^2+x_2^2+x_3^2=1,x_3<0,x_4=0 \end{cases}$$

故而SU(2)群的元素可以看作是SO(3)群的元素的二重覆盖，即SU(2)到SO(3)的同态映射是二对一的。

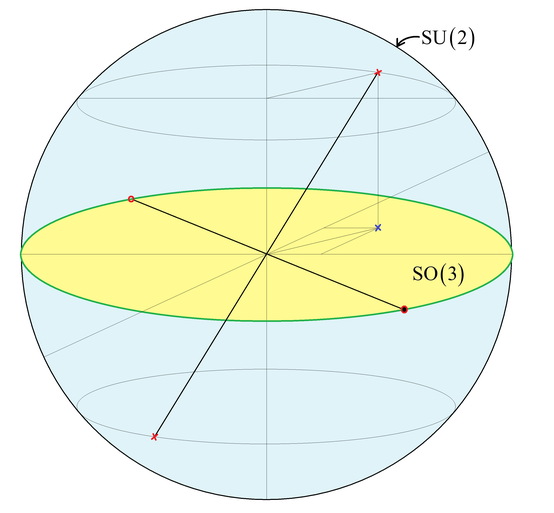
可以参考此图进行理解。将三维球面$S^3$的SU(2)降维到如图所示的蓝色二维球面$S^2$，将对径认同的的三维球体$B^3$的SO(3)降维到如图所示的黄色二维圆盘。此时，非边界（绿色圈）处的蓝色球面上的两个红色叉对应黄色圆盘上的蓝色叉，边界处的两个红色圈（由于径认同）对应黑色圈。

你可能早就见过如下表达式了：

$$SU(2):U(\vec{n},\omega)=e^{i\omega\vec{n}\cdot\vec{\sigma}/2}=\cos(\omega/2)I+i\sin(\omega/2)(n_x\sigma_x+n_y\sigma_y+n_z\sigma_z)$$ $$SO(3):R(\vec{n},\omega)=e^{i\omega\vec{n}\cdot\vec{J}}$$

从这里看，二重覆盖关系是显然的，但是我们在下面推导二者关系的时候使用欧拉角表述，也可以看到二重覆盖关系。

数学描述

通过泡利矩阵：

$$\sigma_x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad \sigma_y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}, \quad \sigma_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$$

可以将二维矩阵和空间矢量联系起来：

$$h=x\sigma_x+y\sigma_y+z\sigma_z=\begin{pmatrix} z & x-iy \\ x+iy & -z \end{pmatrix}$$

现在空间矢量有两种表示形式，且可以被SU(2)和SO(3)群的元素作用。理论上，两种作用应该等价：

$$\vec{r}=\vec{r}(h)\to \begin{cases}\text{使用二维矩阵表示：} & \mathbf{U} h \mathbf{U}^{-1} = h' \\ \text{使用空间矢量表示：} & \mathbf{R} \vec{r} = \vec{r}'\end{cases}\to \vec{r}'=\vec{r}'(h')$$

使用SU(2)元素对该矩阵作用：

$$\mathbf{U} h \mathbf{U}^{-1} = \begin{pmatrix} a & b \\ -b^* & a^* \end{pmatrix} \begin{pmatrix} z & x-iy \\ x+iy & -z \end{pmatrix} \begin{pmatrix} a^* & -b \\ b^* & a \end{pmatrix}=h'$$

使用SO(3)元素对该矢量作用：

$$\mathbf{R} \begin{pmatrix}x \\ y \\ z\end{pmatrix} = \begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}$$

二者联立，可确定了从SU(2)到SO(3)的映射关系：

$$\mathbf{U} =\begin{pmatrix} a & b \\ -b^* & a^* \end{pmatrix}\to R = \left( \begin{array}{ccc} \frac{1}{2}\left(a^{2} + a^{* 2} - b^{2} - b^{*2}\right) & -\frac{i}{2}\left(a^{2} - a^{* 2} + b^{2} - b^{*2}\right) & -\left(a b + a^{*}b^{*}\right) \\ \frac{i}{2}\left(a^{2} - a^{* 2} - b^{2} + b^{*2}\right) & \frac{1}{2}\left(a^{2} + a^{* 2} + b^{2} + b^{*2}\right) & i\left(a^{*} b^{*} - b a\right) \\ a^{*} b + b^{*} a & i\left(a^{*} b - b^{*} a\right) & a a^{*} - b b^{*} \end{array} \right)$$

显然，反解该关系可以得到SO(3)到SU(2)的映射关系：

$$\mathbf{R}= \begin{pmatrix} \cos\alpha\cos\beta\cos\gamma-\sin\alpha\sin\gamma & -\cos\alpha\cos\beta\sin\gamma-\sin\alpha\cos\gamma & \cos\alpha\sin\beta \\ \sin\alpha\cos\beta\cos\gamma+\cos\alpha\sin\gamma & -\sin\alpha\cos\beta\sin\gamma+\cos\alpha\cos\gamma & \sin\alpha\sin\beta \\ -\sin\beta\cos\gamma & \sin\beta\sin\gamma & \cos\beta \end{pmatrix}\to \mathbf{U} = \begin{pmatrix} \cos \frac{\beta}{2} e^{-i(\alpha+\gamma)/2} & -\sin \frac{\beta}{2} e^{-i(\alpha-\gamma)/2} \\ \sin \frac{\beta}{2} e^{i(\alpha-\gamma)/2} & \cos \frac{\beta}{2} e^{i(\alpha+\gamma)/2} \end{pmatrix}$$

其中，$\mathbf{U}$同样可以被分解为三个转动矩阵：

$$\begin{aligned} \mathbf{U} &= \mathbf{U}_{z''}(\gamma) \mathbf{U}_{y'}(\beta) \mathbf{U}_{z}(\alpha)\\ &=\begin{pmatrix} e^{-i\alpha/2} & 0 \\ 0 & e^{i\alpha/2} \end{pmatrix}\begin{pmatrix} \cos\frac{\beta}{2} & -\sin\frac{\beta}{2} \\ \sin\frac{\beta}{2} & \cos\frac{\beta}{2} \end{pmatrix}\begin{pmatrix} e^{-i\gamma/2} & 0 \\ 0 & e^{i\gamma/2} \end{pmatrix}\\ &=\begin{pmatrix} \cos \frac{\beta}{2} e^{-i(\alpha+\gamma)/2} & -\sin \frac{\beta}{2} e^{-i(\alpha-\gamma)/2} \\ \sin \frac{\beta}{2} e^{i(\alpha-\gamma)/2} & \cos \frac{\beta}{2} e^{i(\alpha+\gamma)/2} \end{pmatrix}\end{aligned}$$

SU(2)和SO(3)的不可约表示

求解SU(2)和SO(3)的不可约表示的基本思路如下：

• 构建线性函数空间$\mathcal{L}^j$，$j$是不可约表示的标记；选取每一个函数空间中的基函数组： $$\{\psi_m^j|m=-j,-j+1,\ldots,j\}$$ 其中，基函数可以选取为： $$\psi_m^j(\vec{x})=\psi_m^j(x_1,x_2)=\frac{(-1)^{j-m}}{\sqrt{(j+m)!(j-m)!}}x_1^{j-m}x_2^{j+m}$$
• 定义SU(2)的群元对应的作用算符$\hat P_{\mathbf{U}}$，它可以把多项式基函数映射到另一个多项式函数，具体的作用方式如下（由群的性质限制）： $$\hat P_{\mathbf{U}} \psi_m^j = \psi_m^j(\mathbf{U}^{-1} \vec{x})$$
• 同时，出于基函数组的完备性，任意一个多项式函数都可以用基函数组展开： $$\hat P_{\mathbf{U}} \psi_m^j = \sum_{m'=-j}^{j} D^{(j)}_{m'm} \psi_{m'}^j(\vec{x})$$ 和上式联立，即可得到$D^{(j)}_{m’m}$的具体形式。$D^{(j)}$是SU(2)的以$j$标记的不可约表示。

先计算三种最简单的情况，分别对应$\alpha=0,\beta=0,\gamma=0$。

1. $\alpha=0$时（$\gamma=0$同理）：

   $$\mathbf{U}^{-1}=\begin{pmatrix} e^{i\alpha/2} & 0 \\ 0 & e^{-i\alpha/2} \end{pmatrix};\quad \psi_m^j(\mathbf{U}^{-1} \vec{x})=\psi_m^j(e^{i\alpha/2}x_1,e^{-i\alpha/2}x_2)=\psi_m^j(x_1,x_2)e^{-im\alpha}$$

   所以：

   $$D^{(j)}_{m'm} = e^{-im\alpha}\delta_{m'm}$$

2. $\beta=0$时：

   $$\mathbf{U}^{-1}=\begin{pmatrix} \cos\frac{\beta}{2} & \sin\frac{\beta}{2} \\ -\sin\frac{\beta}{2} & \cos\frac{\beta}{2} \end{pmatrix};\quad \psi_m^j(\mathbf{U}^{-1} \vec{x})=\psi_m^j(\cos\frac{\beta}{2}x_1+\sin\frac{\beta}{2}x_2,-\sin\frac{\beta}{2}x_1+\cos\frac{\beta}{2}x_2)$$

   利用二项式定理展开：

   $$\begin{aligned} &\psi_m^j(\cos\frac{\beta}{2}x_1+\sin\frac{\beta}{2}x_2,-\sin\frac{\beta}{2}x_1+\cos\frac{\beta}{2}x_2)\\ &=\frac{(-1)^{j-m}}{\sqrt{(j+m)!(j-m)!}}(\cos\frac{\beta}{2}x_1+\sin\frac{\beta}{2}x_2)^{j-m}(-\sin\frac{\beta}{2}x_1+\cos\frac{\beta}{2}x_2)^{j+m}\\ &=\frac{(-1)^{j-m}}{\sqrt{(j+m)!(j-m)!}}\left(\sum_{k=0}^{j-m} \binom{j-m}{k} (\cos\frac{\beta}{2}x_1)^{j-m-k}(\sin\frac{\beta}{2}x_2)^k\right)\times\left(\sum_{r=0}^{j+m} \binom{j+m}{r} (-\sin\frac{\beta}{2}x_1)^{j+m-r}(\cos\frac{\beta}{2}x_2)^r\right)\\ &=(-1)^{j-m}\sum_{k=0}^{j-m} \sum_{r=0}^{j+m} (-1)^{j+m-r}\frac{\sqrt{(j+m)!(j-m)!}}{k!r!(j-m-k)!(j+m-r)!} (\cos\frac{\beta}{2})^{j-m-k+r}(\sin\frac{\beta}{2})^{j+m+k-r} x_1^{2j-k-r} x_2^{k+r}\\ \end{aligned}$$

   现在把$x$的幂指数换元为$x_1^{j-m’}x_2^{j+m’}$的形式：

   $$2j-k-r\to j-m';\quad k+r\to j+m'\Rightarrow r=j+m'-k$$

   于是：

   $$\begin{aligned} &\psi_m^j(\cos\frac{\beta}{2}x_1+\sin\frac{\beta}{2}x_2,-\sin\frac{\beta}{2}x_1+\cos\frac{\beta}{2}x_2)\\ &=\sum_{m'=j}^{-j}\sum_{k=0}^{j-m} (-1)^{j-m'+k}\frac{\sqrt{(j+m)!(j-m)!}}{k!(j+m'-k)!(j-m-k)!(m-m'+k)!} (\cos\frac{\beta}{2})^{2j-m+m'-2k}(\sin\frac{\beta}{2})^{m-m'+2k} x_1^{j-m'} x_2^{j+m'}\\ &=\sum_{m'=j}^{-j}\left[\sum_{k=0}^{j-m} (-1)^{k}\frac{\sqrt{(j+m)!(j-m)!(j+m')!(j-m')!}}{k!(j+m'-k)!(j-m-k)!(m-m'+k)!} (\cos\frac{\beta}{2})^{2j-m+m'-2k}(\sin\frac{\beta}{2})^{m-m'+2k}\right]\frac{(-1)^{j-m'}}{\sqrt{(j+m')!(j-m')!}}x_1^{j-m'}x_2^{j+m'}\\ &=\sum_{m'=j}^{-j}\left[D^{(j)}_{m'm}\right]\psi_{m'}^j(x_1,x_2)\\ \end{aligned}$$

   所以：

   $$D^{(j)}_{m'm} = \sum_{k=0}^{j-m} (-1)^{k}\frac{\sqrt{(j+m)!(j-m)!(j+m')!(j-m')!}}{k!(j+m'-k)!(j-m-k)!(m-m'+k)!} (\cos\frac{\beta}{2})^{2j-m+m'-2k}(\sin\frac{\beta}{2})^{m-m'+2k}$$

   考虑阶乘内部不能有负数，因此求和范围为：

   $$D^{(j)}_{m'm} = \sum_{k=\max\{0,m-m'\}}^{\min\{j-m,j+m'\}} (-1)^{k}\frac{\sqrt{(j+m)!(j-m)!(j+m')!(j-m')!}}{k!(j+m'-k)!(j-m-k)!(m-m'+k)!} (\cos\frac{\beta}{2})^{2j-m+m'-2k}(\sin\frac{\beta}{2})^{m-m'+2k}$$

把三种情况组合起来，就是：

$$D^{(j)}_{m'm} = e^{-im'\alpha}e^{-im\gamma}\sum_{k=\max\{0,m-m'\}}^{\min\{j-m,j+m'\}} (-1)^{k}\frac{\sqrt{(j+m)!(j-m)!(j+m')!(j-m')!}}{k!(j+m'-k)!(j-m-k)!(m-m'+k)!} (\cos\frac{\beta}{2})^{2j-m+m'-2k}(\sin\frac{\beta}{2})^{m-m'+2k}$$

另一种表示是：

$$D^{(j)}_{m'm} = \sum_{k=\max\{0,m-m'\}}^{\min\{j-m,j+m'\}} (-1)^{k+m-m'}\frac{\sqrt{(j+m)!(j-m)!(j+m')!(j-m')!}}{k!(j+m'-k)!(j-m-k)!(m-m'+k)!} a^{j+m'-k}{a^*}^{j-m-k}b^{k}{b^*}^{k+m-m'}$$

可以计算出一些具体的不可约表示：

• $j=0$时：是平凡表示： $$D^{(0)} = 1$$
• $j=1/2$时： $$D^{(1/2)}=\begin{pmatrix} \cos \frac{\beta}{2} e^{-i(\alpha+\gamma)/2} & -\sin \frac{\beta}{2} e^{-i(\alpha-\gamma)/2} \\ \sin \frac{\beta}{2} e^{i(\alpha-\gamma)/2} & \cos \frac{\beta}{2} e^{i(\alpha+\gamma)/2} \end{pmatrix}=\begin{pmatrix} a & b \\ -b^* & a^* \end{pmatrix}$$
• $j=1$时： $$D^{(1)}=\begin{pmatrix} \frac12(1+\cos\beta)e^{-i(\alpha+\gamma)}&-\frac1{\sqrt{2}}\sin\beta e^{-i\alpha}&\frac12(1-\cos\beta) e^{-i(\alpha-\gamma)}\\ \frac1{\sqrt{2}}\sin\beta e^{-i\gamma}& \cos\beta& -\frac1{\sqrt{2}}\sin\beta e^{i\gamma}\\ \frac12(1-\cos\beta)e^{i(\alpha-\gamma)}& \frac1{\sqrt{2}}\sin\beta e^{i\alpha}& \frac12(1+\cos\beta)e^{i(\alpha+\gamma)} \end{pmatrix}=\begin{pmatrix} a^2&\sqrt{2}ab& b^2 \\ -\sqrt{2}ab^*& a^*a-b^*b& -\sqrt{2}a^*b \\ {b^*}^2& -\sqrt{2}a^*b^*& {a^*}^2 \end{pmatrix}$$

可以看到，矩阵满足：

$$D^{(j)}(u)=(-1)^{2j} D^{(j)}(-u)$$

所以当$j$为整数时，$D^{(j)}(-u)=D^{(j)}(u)$，而当$j$为半整数时，$D^{(j)}(-u)=-D^{(j)}(u)$。其对应图如下：

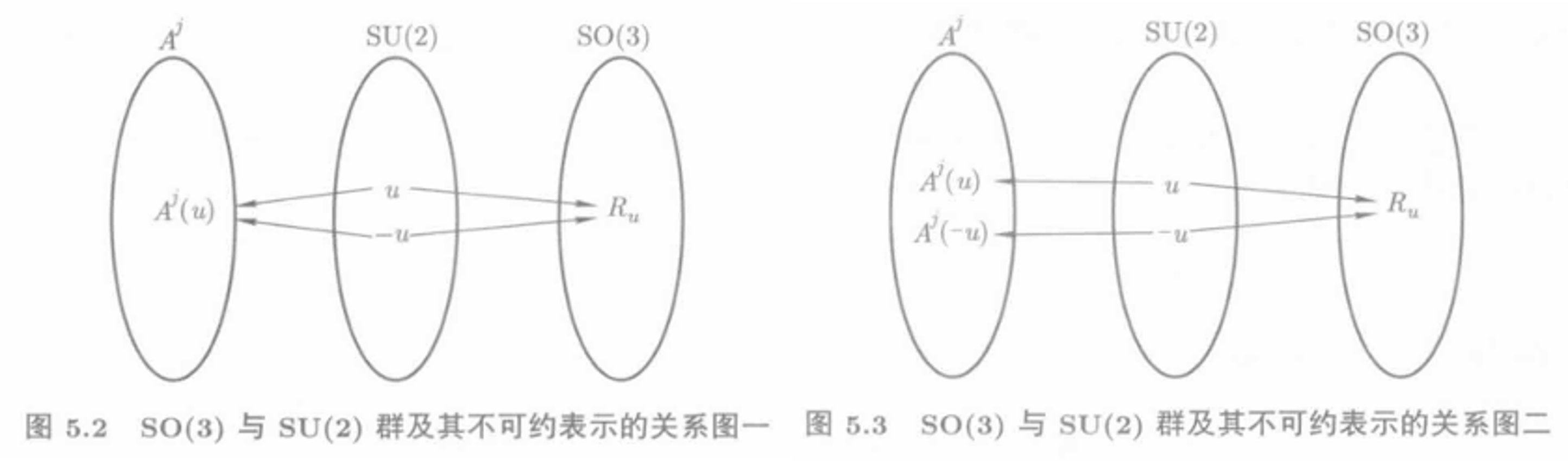
可见当$j$为整数和半整数时，构成SU(2)的所有不可约表示；当$j$为整数时，构成SO(3)的所有不可约表示。