小振动

理论框架

矩阵方程

我们接下来讨论保守力学系统在稳定平衡位形附近作小振动的情况。解析写出拉格朗日量：

$$L=T-V=\sum_{i,j=1}^n \frac{m_{ij}}{2} \dot{x}_i\dot{x}_j- V(x_1, x_2, \cdots, x_n)$$

在平衡位置附近，势能可以用泰勒公式展开：

$$\begin{aligned} V(x_1, x_2, \cdots, x_n) &= V(x_{10}, x_{20}, \cdots, x_{n0}) \\&+ \sum_{i=1}^n \left( \frac{\partial V}{\partial x_i} \right)_0(x_i - x_{i0}) \\ &+ \frac{1}{2} \sum_{i,j=1}^n \left( \frac{\partial^2 V}{\partial x_i \partial x_j} \right)_0 (x_i - x_{i0})(x_j - x_{j0})\\ &+ \cdots \end{aligned}$$

平衡位置处$\left( \dfrac{\partial V}{\partial x_i} \right)_0 = 0$，保留至二次项，取$x_{i0}=0,V(x_{10}, x_{20}, \cdots, x_{n0}) =0$：

$$\begin{aligned} L&=\sum_{i,j=1}^n \frac{m_{ij}}{2} \dot{x}_i\dot{x}_j - \frac{1}{2} \sum_{i,j=1}^n \left( \frac{\partial^2 V}{\partial x_i \partial x_j} \right)_0 (x_i - x_{i0})(x_j - x_{j0})\\ &=\frac12 \dot{\vec{x}}^T \mathbf{M} \dot{\vec{x}} - \frac{1}{2} \vec{x}^T \mathbf{K} \vec{x} \end{aligned}$$

$\mathbf{M}$和$\mathbf{K}$是天然的正定二次型，这点将在后续证明特征值小于零用到。代入欧拉-拉格朗日方程：

$$\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}_i} \right) - \frac{\partial L}{\partial x_i} = 0$$

得到

$$\mathbf{M}\ddot{\vec{x}} + \mathbf{K} \vec{x} = 0$$

对于$n$个自由度的系统，该矩阵方程最多确定n个特征值$\lambda_i$，满足：

$$\dot{\vec{x}}_i=\lambda_i \vec{x}_i,\ddot{\vec{x}}_i = \lambda_i^2 \vec{x}_i$$

将其代入矩阵方程，得到特征值方程：

$$(\mathbf{M} \lambda_i^2 + \mathbf{K})\vec{x}_i = 0$$

这个方程若有非零解，则必须满足行列式为零：

$$\det(\mathbf{M} \lambda_i^2 + \mathbf{K}) = 0$$

最终的运动解可以使用特征解的线性组合表示：

$$\vec{x}(t) = \sum_{i=1}^n c_i\vec{x}_{i} e^{\lambda_i t}$$

特征频率

从该方程：

$$(\mathbf{M} \lambda_i^2 + \mathbf{K})\vec{x} = 0$$

进行变形，可以得到：

$$\lambda^2_i = -\frac{\vec{x}^T \mathbf{K} \vec{x}}{\vec{x}^T \mathbf{M} \vec{x}}<0$$

由于$\mathbf{K}$是正定的，$\vec{x}^T \mathbf{K} \vec{x}>0$，而$\mathbf{M}$也是正定的，$\vec{x}^T \mathbf{M} \vec{x}>0$，因此特征值$\lambda_i$都是小于零的，说明都是虚数。引入特征频率：

$$\lambda_i = i \omega_i$$

最终的运动解可以写成：

$$\vec{x}(t) = \sum_{i=1}^n c_i \vec{x}_{i} e^{i \omega_i t}$$

相应的矩阵方程变为：

$$\det(-\mathbf{M} \omega_i^2 + \mathbf{K}) = 0$$

不难发现，求解特征频率的过程实际上是求解一个广义特征值问题：

$$\mathbf{K}\vec{x}=\omega_i^2\mathbf{M}\vec{x}$$

我们的目的是确定特征值矩阵$\mathbf{\Omega}^2$和相似变换矩阵$\mathbf{U}$：

$$\mathbf{\Omega}^2 = \text{diag}(\omega_1^2, \omega_2^2, \cdots, \omega_n^2)，\mathbf{U}=[\vec{x}_1, \vec{x}_2, \cdots, \vec{x}_n]$$

此时，可令：

$$\mathbf{U}^T \mathbf{M} \mathbf{U} = \mathbf{I}$$

同时：

$$\mathbf{U}^T \mathbf{K} \mathbf{U} = \mathbf{\Omega}^2$$

这意味着两个矩阵是同时被对角化的。代入拉格朗日量：

$$\begin{aligned} L &= \frac{1}{2} \dot{\vec{x}}^T \mathbf{M} \dot{\vec{x}} - \frac{1}{2} \vec{x}^T \mathbf{K} \vec{x} \\&= \frac{1}{2} \dot{\vec{y}}^T \mathbf{U}^T \mathbf{M} \mathbf{U} \dot{\vec{y}} - \frac{1}{2} \vec{y}^T \mathbf{U}^T \mathbf{K} \mathbf{U} \vec{y}\\&= \frac{1}{2} \dot{\vec{y}}^T \dot{\vec{y}} - \frac{1}{2} \vec{y}^T \mathbf{\Omega}^2\vec{y}\\&=\sum_i(\frac12\dot{y_i}^2-\frac12\omega_i^2y_i^2)\\&=\sum_i L_i \end{aligned}$$

至此，我们将拉格朗日量分解为$n$个独立的简正模式系统。

双摆

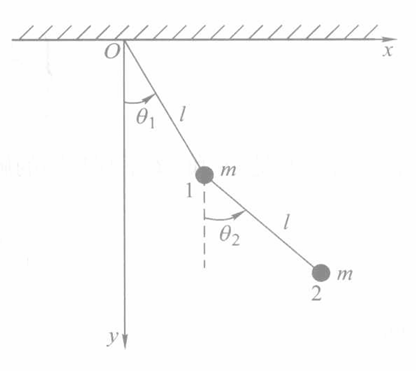
此前我们曾得到了双摆的拉格朗日量：

$$L = T - V=\frac12(m_1+m_2)l_1^2\dot{\theta}_1^2 + m_2 l_1 l_2 \dot{\theta}_1 \dot{\theta}_2 \cos(\theta_1 - \theta_2) + \frac12 m_2 l_2^2 \dot{\theta}_2^2 + (m_1 + m_2) g l_1\cos\theta_1+m_2 g l_2\cos\theta_2$$

在小角近似下：

$$L = T - V=\frac12(m_1+m_2)l_1^2\dot{\theta}_1^2 + m_2 l_1 l_2 \dot{\theta}_1 \dot{\theta}_2 + \frac12 m_2 l_2^2 \dot{\theta}_2^2 -\frac12 (m_1 + m_2) g l_1\theta_1^2-\frac12m_2 g l_2\theta_2^2$$

将其写成矩阵形式：

$$\mathbf{M} = \begin{pmatrix} (m_1 + m_2) l_1^2 & m_2 l_1 l_2 \\ m_2 l_1 l_2 & m_2 l_2^2 \end{pmatrix}, \quad \mathbf{K} = \begin{pmatrix} (m_1 + m_2) g l_1 & 0\\ 0& \frac12m_2 g l_2 \end{pmatrix}$$

求解特征值方程：

$$\det(-\mathbf{M} \omega^2 + \mathbf{K}) = 0$$

得到以下方程：

$$l_1l_2x^2-\frac{m_1+m_2}{m_1}g(l_1+l_2)x+\frac{m_1+m_2}{m_1}g^2=0,x=\omega^2$$

解得：

$$\omega^2=\frac{g}{2l_1l_2}\left[ \frac{m_1+m_2}{m_1}(l_1+l_2) \pm \sqrt{\left( \frac{m_1+m_2}{m_1} \right)^2(l_1+l_2)^2 - 4\frac{m_1+m_2}{m_1}l_1l_2} \right]$$

对于质量相等$m_1=m_2=m$，摆长相等的情况，可以进一步简化为：

$$\omega^2=\frac{g}{l}\left[2 \pm \sqrt{2} \right]$$

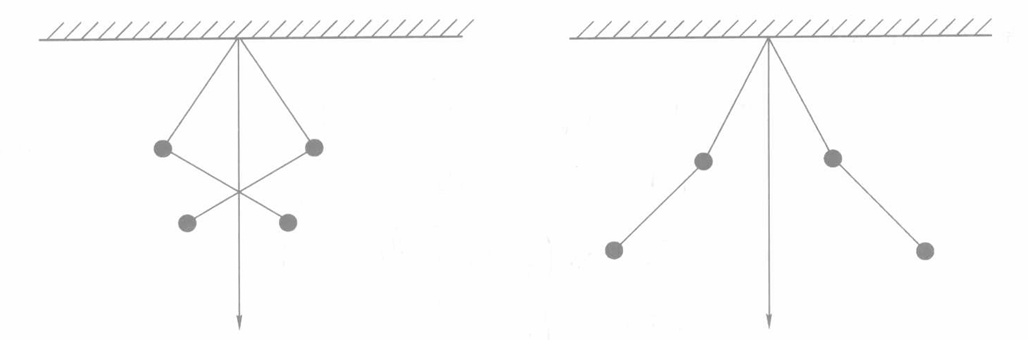
分别对应两种振动模式：

耦合摆

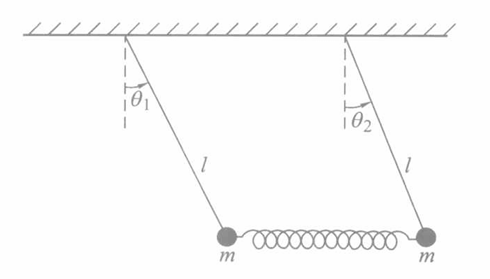
写出拉格朗日量：

$$T =\frac12 m_1 l^2 \dot{\theta}_1^2 + \frac12 m_2 l^2 \dot{\theta}_2^2$$ $$V = \frac12 k l^2(\theta_1 - \theta_2)^2 +\frac12 m_1 g l \theta_1^2 +\frac12 m_2 g l \theta_2^2$$

将其写成矩阵形式：

$$\mathbf{M} = \begin{pmatrix} m_1 l^2 & 0 \\ 0 & m_2 l^2 \end{pmatrix}, \quad \mathbf{K} = \begin{pmatrix} k l^2 + m_1 g l & -k l^2 \\ -k l^2 & k l^2 +m_2 g l \end{pmatrix}$$

解得：

$$\omega_1^2 = \frac{k(m_1+m_2)}{m_1 m_2 } +\frac{g}{l}$$ $$\omega_2^2 = \frac{g}{l}$$

分别对应两种振动模式：