刚体运动学

刚体的自由度

刚体指的是系统内各质点间距离保持不变的物体。这是一种完整约束，因而可以参与自由度的减少。常见的运动对应的自由度如下：

运动类型	平动自由度	旋转自由度	总自由度
定轴转动	0	1	1
定点转动	0	3	3
平动	3	0	3
平面平行运动	2	1	3

刚体的转动描述

描述刚体的平动是简单的，只需要三个质心坐标$(x_c, y_c, z_c)$即可。描述刚体的转动是复杂的，一种被动的观点是描述刚体坐标架的转动矩阵$\mathbf{U}$：

$\begin{pmatrix} i'\\ j'\\ k' \end{pmatrix} = \mathbf{U} \begin{pmatrix} i\\ j\\ k \end{pmatrix}$

这是一个实正交矩阵。另一种主动观点为描述转动矢量或张量，而坐标架不动。

显然，刚体的位置和转动的次序是相关的，即矩阵乘法不能交换次序：

$\mathbf{U}_1 \mathbf{U}_2 \neq \mathbf{U}_2 \mathbf{U}_1$

每一个旋转操作对应一个逆操作：

$\mathbf{U}^{-1} = \mathbf{U}^T$

欧拉转动定理告诉我们，对于任意一个转动操作$\mathbf{U}$，都存在一根轴$\mathbf{n}$，使得：

$\mathbf{U}\mathbf{n} = \mathbf{n}$

这一点可以通过证明$\det (\mathbf{U}-\mathbf{I})=0$来得到。

证明：
$\begin{aligned} \det (\mathbf{U}-\mathbf{I}) &= \det (\mathbf{U}-\mathbf{U}\mathbf{U}^T) \\ &=\det (\mathbf{U})\det (\mathbf{I}-\mathbf{U}^T)\\ &=\det (\mathbf{I}-\mathbf{U}^T) \\ &=\det (\mathbf{I}-\mathbf{U}) \\ &= (-1)^3\det (\mathbf{U}-\mathbf{I}) = 0 \end{aligned}$

因此，任意一个转动操作都简化为了一根拥有两个自由度的轴和一个自由度的转动角度。以z轴为例：

$\mathbf{U} = \begin{pmatrix} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{pmatrix}$

其本征值分别为：

$\lambda_1=1, \quad \lambda_2 = e^{i\theta}, \quad \lambda_3 = e^{-i\theta}$

对于无三维任意轴的转动，可以用欧拉角分三步描述如何从坐标轴$XYZ$转到$xyz$：

alt

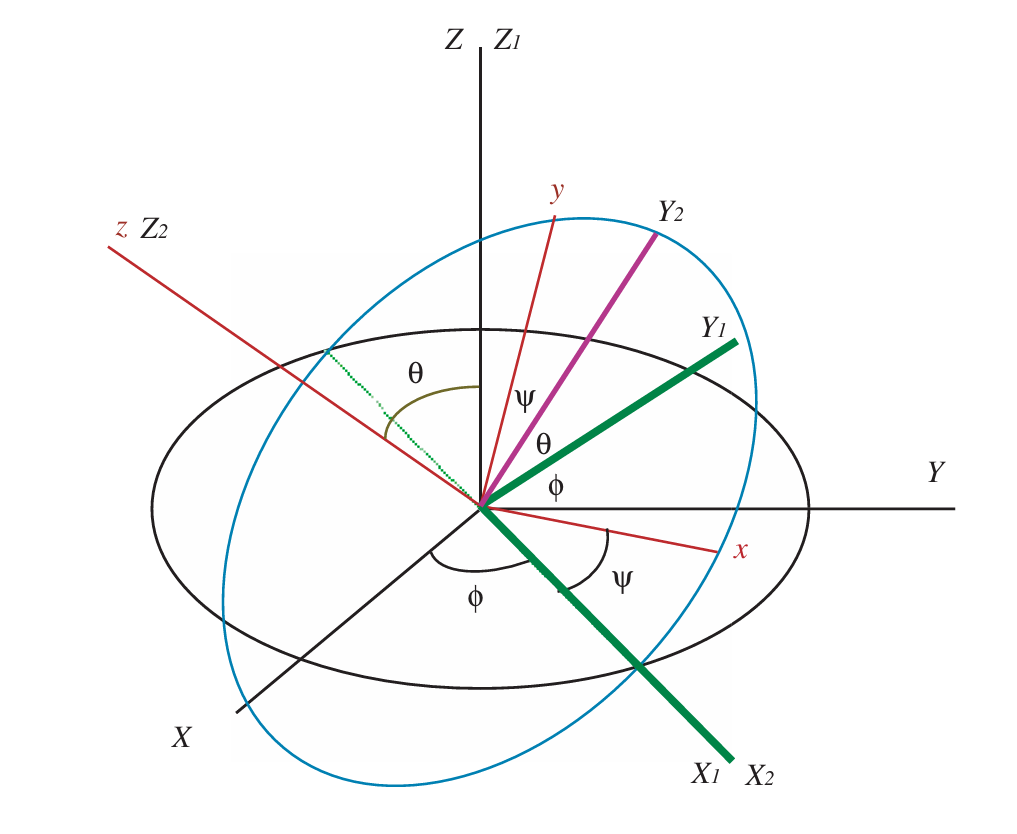
先绕着$Z$轴转动$\phi$角度（进动角），得到新的坐标架$X_1Y_1Z_1$；
再绕着$X_1$轴转动$\theta$角度（章动角），得到新的坐标架$X_2Y_2Z_2$；
最后绕着$Z_2$轴转动$\psi$角度（自转角），得到新的坐标架$xyz$。

三个转动矩阵分别为：

$\mathbf{U}_1 = \begin{pmatrix} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{pmatrix}, \quad \mathbf{U}_2 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta \end{pmatrix}, \quad \mathbf{U}_3 = \begin{pmatrix} \cos \psi & \sin \psi & 0 \\ -\sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{pmatrix}$

最终的转动矩阵为：

$\mathbf{U} = \mathbf{U}_3 \mathbf{U}_2 \mathbf{U}_1 = \begin{pmatrix} \cos \phi \cos \psi - \sin \phi \sin \psi \cos \theta & \sin \phi \cos \psi + \cos \phi \sin \psi \cos \theta & \sin \theta \sin \psi\\ -\sin \phi \cos \psi - \sin \phi \cos \psi \cos \theta & -\sin \phi \sin \psi + \cos \phi \cos \psi \cos \theta & \sin \theta \cos \psi\\ \sin \theta \sin \phi & -\sin \theta \cos \phi & \cos \theta \end{pmatrix}$

刚体的转动速度描述

定义转动速度从主动的观点更加合适。考虑已知转轴$\hat{n}$和转动角度$\phi$，则原有矢量$\vec{r}$在转动后变为：

$\vec{r}' = (\vec{r}\cdot\hat{n})\hat{n}+ [\vec{r}-(\vec{r}\cdot\hat{n})\hat{n}] \cos \phi + (\hat{n} \times \vec{r})\sin \phi$

考虑无穷小转动$\delta \phi$，则有：

$\vec{r}' = \vec{r} + \delta \phi (\hat{n} \times \vec{r})$

转动速度可以定义为：

$\vec{v}=\dot{\phi} (\hat{n} \times \vec{r})=\vec{\omega}\times\vec{r}$

其中$\vec{\omega}=\dot{\phi}\hat{n}$是转动速度矢量。

无穷小的转动是可以交换的，因此虽然角位移不是一个矢量，但角速度可以定义为矢量。

利用图解法，可以归纳角速度和欧拉角的关系：

$\begin{cases} \Omega_x=\dot{\phi}\sin\theta\sin\psi + \dot{\theta}\cos\psi\\ \Omega_y=\dot{\phi}\sin\theta\cos\psi - \dot{\theta}\sin\psi\\ \Omega_z=\dot{\phi}\cos\theta + \dot{\psi} \end{cases}$

刚体的转动惯量

利用上式定义的转动速度，可以定义刚体的转动角动量：

$\begin{aligned} L&=\sum_i m_i (\vec{r}_i \times \vec{v}_i) \\ &= \sum_i m_i (\vec{r}_i \times (\vec{\omega} \times \vec{r}_i))\\ &= \sum_i m_i (\vec{r}_i \cdot \vec{r}_i) \vec{\omega} - \sum_i m_i (\vec{r}_i \cdot \vec{\omega}) \vec{r}_i\\ &=\sum_i m_i (x_i^2+y_i^2+z_i^2) (\omega_x\hat{i}+\omega_y\hat{j}+\omega_z\hat{k}) - \sum_i m_i(x_i\omega_x+y_i\omega_y+z_i\omega_z) (x_i\hat{i}+y_i\hat{j}+z_i\hat{k})\\ &=\mathbf{I} \vec{\omega} \\ \end{aligned}$

其中，$\mathbf{I}$是转动惯量张量：

$\mathbf{I} = \begin{pmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{pmatrix} = \sum_i m_i \begin{pmatrix} y_i^2+z_i^2 & -x_iy_i & -x_iz_i \\ -x_iy_i & x_i^2+z_i^2 & -y_iz_i \\ -x_iz_i & -y_iz_i & x_i^2+y_i^2 \end{pmatrix}$

显然这是一个实对称矩阵，因此可以对其进行对角化：

$\mathbf{I} = \begin{pmatrix} I_1 & 0 & 0 \\ 0 & I_2 & 0 \\ 0 & 0 & I_3 \end{pmatrix}$

相应的坐标系被称为惯量主轴，$I_1, I_2, I_3$分别是主转动惯量。

如果已经知道了一个刚体关于质心的转动惯量$I_c$，则可以通过平行轴定理计算出距离$d$外的平行于质心轴的转动惯量：

$I = I_c + m d^2$

证明：
$\begin{aligned} I &= \sum_i m_i (\vec{r}_i+\vec{d})^2 \\ &= \sum_i m_i (\vec{r}_i^2 + 2\vec{r}_i \cdot \vec{d} + \vec{d}^2) \\ &= \sum_i m_i \vec{r}_i^2 + 2\vec{d} \cdot \sum_i m_i \vec{r}_i + \sum_i m_i \vec{d}^2 \\ &= I_c + m \vec{d}^2 \end{aligned}$

如果已知一个平面刚体关于垂直于平面的轴的转动惯量$I_z$，则可以通过垂直轴定理给出平行于平面的互相垂直轴的转动惯量的关系：

$I_z= I_x + I_y$

证明：
$\begin{aligned} I_z &= \sum_i m_i (x_i^2+y_i^2) \\ &= \sum_i m_i x_i^2 + \sum_i m_i y_i^2 \\ &= I_x + I_y \end{aligned}$
常见刚体的转动惯量：

长为$L$，质量为$m$的细长杆绕着其中心垂直于杆的轴的转动惯量为： $I_c = \frac{1}{12} m L^2$

长为$L$，质量为$m$的细长杆绕着其一端垂直于杆的轴的转动惯量为： $I = \frac{1}{3} m L^2$

半径为$R$，质量为$m$的圆盘绕着其中心垂直于盘面的轴的转动惯量为： $I_c = \frac{1}{2} m R^2$

半径为$R$，质量为$m$的圆盘绕着其一端垂直于盘面的轴的转动惯量为： $I = \frac{1}{2} m R^2 + m \left(\frac{R}{2}\right)^2 = \frac{3}{4} m R^2$

半径为$R$，质量为$m$的圆盘绕着平面上的中心轴的转动惯量为： $I = \frac{1}{4} m R^2$

刚体的动能

定点运动的刚体的转动动能可以写为：

$\begin{aligned} T &= \frac{1}{2} \sum_i m_i \vec{v_i}^2 \\ &= \frac{1}{2} \sum_i m_i \vec{v_i}\cdot (\vec{\omega}\times \vec{r}_i) \\ &= \frac{1}{2} \sum_i m_i \vec{\omega}\cdot (\vec{r}_i\times \vec{v_i}) \\ &= \frac{1}{2} \vec{\omega}\cdot \sum_i m_i (\vec{r}_i\times \vec{v_i}) \\ &= \frac{1}{2} \vec{\omega}\cdot \vec{L}\\ &= \frac{1}{2} \mathbf{\omega}^T\mathbf{I}\mathbf{\omega}\\ \end{aligned}$

一般可以简化为$T=\frac12 I \omega^2$，其中$I$是转动惯量，$\omega$是转动速度。

对于一般运动，刚体的动能可以写为：

$\begin{aligned} T &= \frac{1}{2} \sum_i m_i (\vec{v}_0+\vec{\omega}\times \vec{r}_i)^2 \\ &= \frac{1}{2} \sum_i m_i \vec{v}_0^2 + \sum_i m_i \vec{v}_0\cdot (\vec{\omega}\times \vec{r}_i) + \frac{1}{2} \sum_i m_i (\vec{\omega}\times \vec{r}_i)^2 \\ &= \frac{1}{2} m v_c^2 + \vec{\omega}\cdot \vec{L}_{\vec{v}_0} + T_{rot} \\ \end{aligned}$

其中，$v_c$是质心的速度。当且仅当旋转轴穿过质心的时候，$\vec{L}_{\vec{v}_0}$为零，这时候，刚体的动能可以简化为：

$T = \frac{1}{2} m v_c^2 + \frac{1}{2}I \omega^2$

其中，$m$是刚体的质量。

刚体力学