Bloch电子动力学
在能带论的基础上,我们不再满足经典的Drude模型和Sommerfeld模型,而是希望基于能带论建立半经典模型。
Bloch电子动力学
Bloch电子的速度
我们此前已经证明,周期性势场中的单电子薛定谔方程的本征函数可以写成Bloch波形式:
其中,$u_k^n(\vec{r})$是一个周期函数,满足$u_k^n(\vec{r}+\vec{R})=u_k^n(\vec{r})$,$\vec{R}$为晶格矢量。总的来说,Bloch波是由$u_k^n(\vec{r})$调幅的平面波。
将Bloch波代入薛定谔方程,得到:
这里存在一个等效哈密顿量:
它告诉我们,平面波部分贡献了动量$\hbar \vec{k}$,这部分动量称为晶格动量,它是电子动量$\hat{p}\psi=(\hat{p}+\hbar \vec{k})u$的一部分。
按照速度的定义,电子的速度为:
同时,对$\hat{H}_k u_k^n(\vec{r})=E_n(k)u_k^n(\vec{r})$两边求导$\nabla_{\vec{k}}$,得到:
左乘$u_k^{n*}(\vec{r})$,得到:
由$\hat{H}_k$算符的厄密性,得到:
自然得到速度公式:
由于Bloch波是与时间无关的定态,则平均速度会永远保持不变,意思就是理想晶体金属拥有无穷大的电导率。实际上,由于缺陷的存在(或者晶格的振动),电子会受到散射,不能被无限加速。这一机制可以被碰撞和弛豫时间描述,我们在 金属电子论 已然谈到(尽管动机和假设不同)。
半经典模型
每个电子具有确定的位置$\vec{r}$、波矢$\vec{k}$和能带指标$n$,对于给定的能带$E_n(k)$,电子在外电场$\vec{E}(\vec{r},t)$和磁场$\vec{B}(\vec{r},t)$下的运动遵循以下规则:
- 能带指标是守恒量,忽略电子跃迁的可能;
- 电子的速度为:
- 电子的动力学方程:
从两条基本方程出发,可以导出加速度公式:
写入动量,可以得到更有物理意义的形式:
这样就得到了有效质量的表达式:
我们在 能带论 中已经讨论过了简单立方晶体的有效质量。注意到可以通过合理选取主轴使得有效质量张量对角化,得到有效质量的三个主值:
对于上下延展的能带,从表达式可知有效质量较小;而对于横向延展的能带,有效质量较大。从紧束缚模型的角度看,是因为后者更为局域,就像质量较大的粒子一样。
在 金属电子论 中提到了电子比热容的表达式:
所以有效质量可以通过测量比热容来得到:
恒定电场磁场中Bloch电子的运动
恒定电场
对于自由电子,由于$\hbar\vec{k}$就是电子动量,所以电子会被无线加速。
对于Bloch电子,速度的变化为:
然而速度函数是一个有界周期函数,所以电子的速度会在一个周期内来回振荡,周期为:
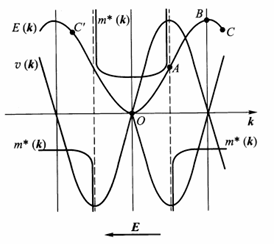
在直流电场下产生交流电流,被称为Bloch振荡(因为晶格缺陷,散射周期$\tau$远小于布里渊区周期$T$)。具体来说,电子越过A点后,有效质量变为负数,则速度不增反减,越过C点后,进入C’点,开启新的周期运动。
显然,如果能带被填满,那么由于$\vec{k}$和$-\vec{k}$的对称性,电子的平均速度为0,电流为0。如果不加入散射机制,能带被部分填充时,也不会有净电流。必须让散射机制起作用,才能打破这种对称性,让电子停留在非对称态。

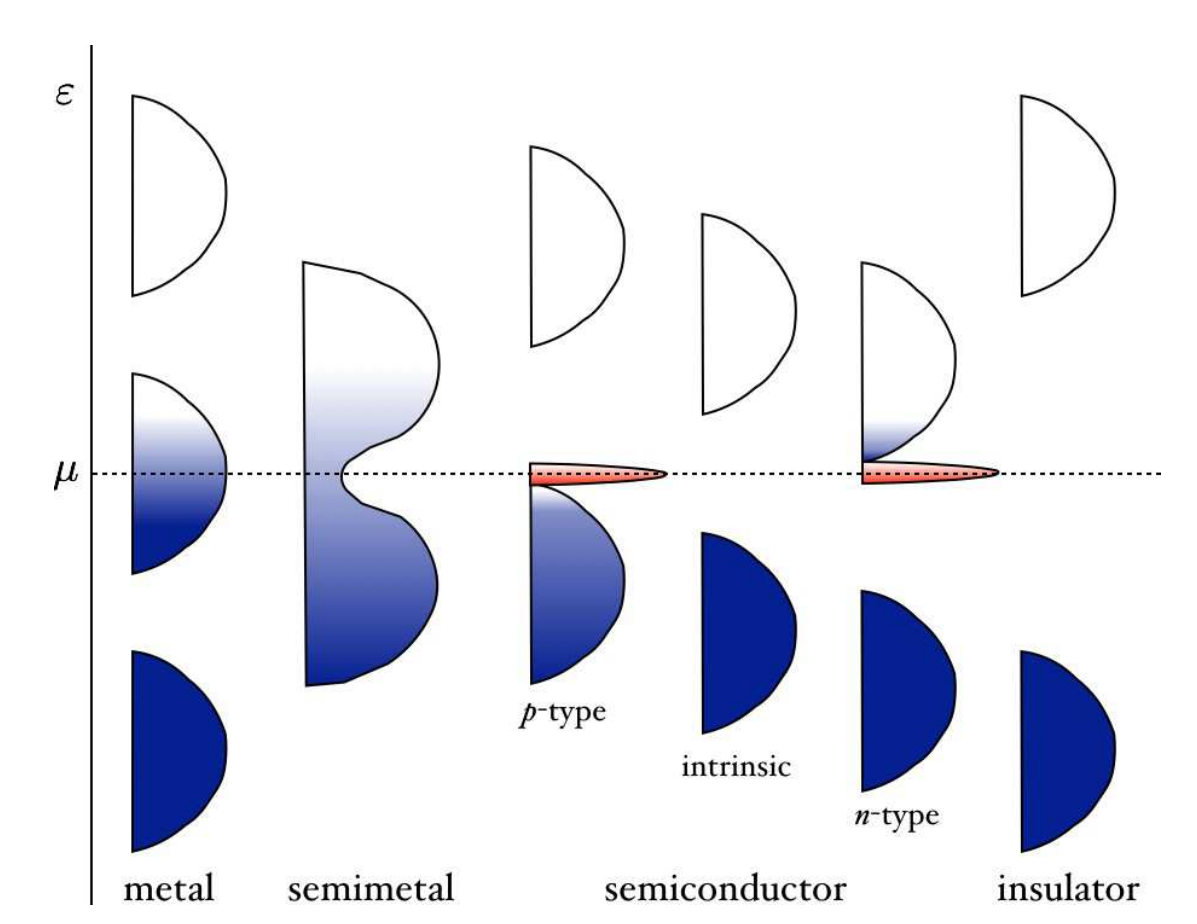
利用非经典模型可以结合能带解释导电现象。对于导体(conductor),其费米面刚好在能带之内;对于半导体(semiconductor)和绝缘体(insulator),费米面在带隙之中,但是半导体的带隙较小,一般在$0\sim2eV$之间,绝缘体的带隙较大。半导体在有限温度时,价带(valence band)中的部分电子被热激发到导带(conduction band)中,形成导电电子和空穴。杂质贡献不明显的叫做本征半导体(intrinsic),杂质贡献明显的叫做非本征半导体(extrinsic)。
考虑一个含有n个电子、N个元胞的晶体,每个能带上有2N个能态(考虑泡利不相容原理)。由于$\frac{n}{N}$表示每个元胞的电子个数,是个整数;那么$\frac{n}{2N}$表示被电子占据的平均能态数,是个整数或半整数。也就是说,对于理想晶体,只有全填充和半填充两种情况。
这样说来,二价金属应当是绝缘体,但由于s带和p带的重叠,形成了一个小的导带,所以二价金属仍然是导体。
恒定磁场
不考虑散射,电子在k空间的运动可以写为:
显然,上面这条式子暗示了两件事情:
- $\hbar\dot{\vec{k}}\cdot \vec{B}=0$,即$\dot{\vec{k}}$与$\vec{B}$垂直($\vec{k}_z$是个守恒量);
- $\hbar\dot{\vec{k}}\cdot \vec{v}=0$,即$\dot{\vec{k}}$与$\vec{v}$垂直(结合$\vec{v}=\frac{1}{\hbar} \nabla_{\vec{k}}E_n(k)$,这说明能量守恒);
因此,电子在k空间的运动轨道是等能面和与磁场垂直的平面的交线。自由电子的等能面是一个球面,因此自由电子在k空间的运动轨道是圆形,对应到实空间就是螺旋轨道。
Bloch电子的等能面不是一个球面,所以其运动轨道会更加复杂,可能呈现出非圆形的轨迹,甚至是非闭合的,具体见下图:
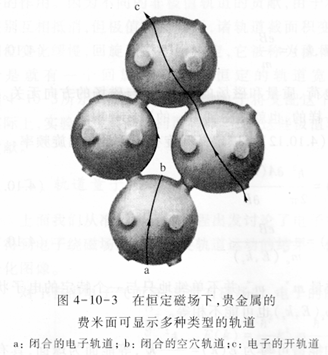
可以写出理论上电子的运动周期:
由于k空间的能量满足:
因此可以得到:
其中,$A(E,\vec{k}_z)$是等能面的面积,积分$\oint{\Delta kdk}$刚好是两个轨道之间的面积。将周期写为$T=\frac{2\pi}{\omega_c}$,可以得到等效回旋质量的定义:
以自由电子为例,能量为$E=\frac{\hbar^2 k^2}{2m}$,在最大圆上的等效回旋质量为:
对于Bloch电子,费米面非常复杂,一般考虑横截面为极值的轨道,称为极值轨道。在极值轨道上,等效回旋质量和回旋频率几乎恒定。
以上图像都是准经典的,实际上,描述电子在磁场中的运动应当用到 Quantum Dynamics & Quantum Geometry 中学到的朗道能级:
其中,$\omega_c=\frac{eB}{m}$是朗道频率。朗道能级的分布是离散的,能级间隔为$\hbar\omega_c$,因此在磁场中电子的运动轨迹是量子化的。
利用朗道能级可以解释De Haas-van Alphen效应。体系的磁矩随体系能量和外场的关系为:
如果用准经典模型,则体系的自由能不会随磁场改变,因为电子密集填充在费米面下。但是对于朗道能级,由于磁场变大时朗道能级间隔变大,体系的能量会类似下图经历周期性变化,尤其在极值轨道非常明显:
这种磁矩随磁场的变化被称为De Haas-van Alphen效应,利用它可以测量机制轨道的面积,进而测定费米面的形状。
霍尔效应
单能带模型
考虑散射的情况下,电子同时在电场和磁场中运动:
定态时,电子的速度为:
电流密度$\vec{J}=-ne\vec{v}$,写成矩阵的形式:
其中$\sigma_0=\dfrac{n\tau e^2}{m}$是零场电导,我们在 金属电子论 中推到过。
这里的电阻率是一个张量,同理,可以写出电导率的张量:
当电流只能从$x$方向流动时,$J_y=0$,得到霍尔效应:
霍尔系数为:
与此同时,同方向的电流密度为:
这说明磁场的增加并没有带来额外的电阻(即磁滞电阻)。这是因为该理论忽略了能带的结构,认为所有电子具有一样的速度、质量和弛豫时间。我们以一个简单的双能带模型来说明。
双能带模型
考虑一个双能带模型,电子具有两种有效质量和弛豫时间:
总的电流密度为$\vec{J}=\vec{J}_{1}+\vec{J}_{2}$:
- 低磁场情况下,$\omega_1\tau_1\ll 1$,$\omega_2\tau_2\ll 1$,可以近似为:解$J_y=0$得到:霍尔系数为:这意味着总的霍尔系数是各个能带霍尔系数的加权平均。同理,可以算出此时的电阻率(不给出计算过程):其中,$\mu_i=\frac{e\tau_i}{m_i}$是各个电子的迁移率。当两种电子的迁移率相等的时候,上述式子退化为$\Delta\rho=0$,即没有磁滞电阻。
- 高磁场情况下,$\omega_1\tau_1\gg 1$,$\omega_2\tau_2\gg 1$,可以得到:这说明在高磁场下,霍尔系数不再是各个能带霍尔系数的加权平均,而是总的载流子浓度的倒数。此时,磁滞电阻为:趋向于一个饱和值。