激光原理

激光(Laser)的全名是受激光辐射放大(Light Amplification by Stimulated Emission of Radiation)，是通过受激辐射过程产生的相干光源。激光具有高度的单色性、方向性和相干性。

跃迁理论

光的发射和吸收是光场与物质作用的结果。光场与物质作用使得组成物质的原子 （或分子）从一个本征态 （能级） 跃迁到另一个本征态，与此伴随着光场某一波型内增加或减少一个光子，这就是单光子的发射和吸收行为，这种行为包括三种基本过程，即自发辐射、受激辐射和受激吸收。

自发辐射

原子中处于高能级$E_2$的电子自发地向低能级$E_1$跃迁，并发射出一个能量为$h\nu=E_2-E_1$的光子的现象，叫自发辐射。

自发辐射的速度可以用以下公式描述：

$$\frac{dN_2}{dt}|_{sp}=-A_{21}N_2$$

对于没有外界扰动的情况下，可以描述为：

$$N_2(t)=N_2(0)e^{-A_{21}t}$$

平均寿命为：

$$\tau_{21}=\frac{1}{A_{21}}$$

常见的自发辐射的例子包括荧光和磷光。前者的寿命大概在纳秒级别，而后者的寿命由于存在自旋禁阻，大概在秒量级。

受激辐射

当外来光子的频率满足$h\nu=E_2-E_1$时，使原子中处于高能级的电子在外来光子的激发下向低能级跃迁而发光的现象，叫受激辐射。

受激辐射的速度可以用以下公式描述：

$$\frac{dN_2}{dt}|_{sp}=W_{21}N_2$$

其中，受激辐射速度和外来光场的单色能量密度正比：

$$W_{21}=B_{21}\rho(\nu)$$

受激吸收

当外来光子的频率满足$h\nu=E_2-E_1$时，使原子中处于低能级的电子在外来光子的激发下向高能级跃迁的现象，叫受激吸收。

受激吸收的速度可以用以下公式描述：

$$\frac{dN_1}{dt}|_{sp}=-W_{12}N_1$$

其中，受激吸收速度和外来光场的单色能量密度正比：

$$W_{12}=B_{12}\rho(\nu)$$

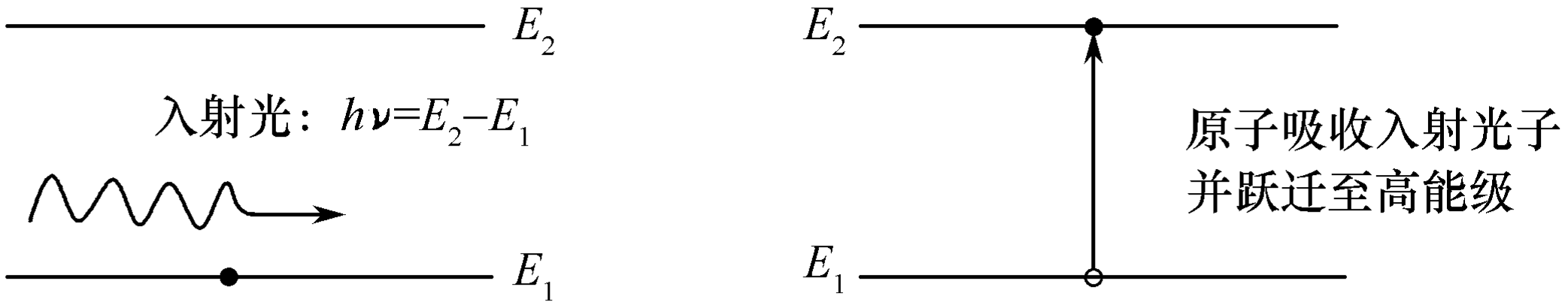
三个辐射和吸收速率，也叫爱因斯坦系数。

三个爱因斯坦系数的关系

处于热平衡条件时，三个系数满足：

$$A_{21}N_2+B_{21}\rho(\nu)N_2=B_{12}\rho(\nu)N_1$$

由此可以得到：

$$\frac{N_2}{N_1}=\frac{B_{12}\rho(\nu)}{A_{21}+B_{21}\rho(\nu)}$$

由玻尔兹曼分布得：

$$\frac{N_2}{N_1}=\frac{g_2}{g_1}e^{-\frac{E_2-E_1}{kT}}$$

联立反解出$\rho(\nu)$：

$$\rho(\nu)=\frac{A_{21}}{B_{21}}\dfrac{1}{\dfrac{B_{12}g_1}{B_{21}g_2}e^{\frac{E_2-E_1}{kT}}-1}$$

此外，根据黑体辐射公式：

$$\rho(\nu)=\frac{8\pi h\nu^3}{c^3}\frac{1}{e^{\frac{h\nu}{kT}}-1}$$

联立可得：

$$\frac{A_{21}}{B_{21}}=\frac{8\pi h\nu^3}{c^3}$$ $$g_1B_{12}=g_2B_{21}$$

光的增益

忽略自发辐射，令$g_1=g_2$，则有：

$$B\triangleq B_{12}=B_{21}$$

一定长度的介质中，满足：

$$\frac{dI}{dz}=B(N_2-N_1)I\Rightarrow I(z)=I(0)e^{B(N_2-N_1)z}$$

意味着要想实现激光放大，必须满足$N_2>N_1$，即必须有粒子数反转。根据玻尔兹曼分布，这意味着$T<0$。要想打破热平衡状态，必须向介质内输入能量，这也意味着光的放大不打破能量守恒。

这就像蓄水库，长期的蓄水是为了放水的时候足够快。

粒子数反转

想要实现粒子数反转，必须满足以下条件：

1. 介质中至少存在多个能级；（水库有高低差）
2. 激发态的能级寿命要长；（水库要稳定）

下面证明二能级系统无法实现粒子数反转。

二能级系统

对于激发态：

$$\frac{dN_2}{dt}=-A_{21}N_2-B\rho(\nu)N_2+B\rho(\nu)N_1$$

稳态时：

$$\frac{N_2}{N_1}=\frac{B\rho(\nu)}{A_{21}+B\rho(\nu)}<1$$

这意味着二能级系统无法实现粒子数反转。

直观理解，由于自发辐射的存在，向下跃迁的速率总会大于向上跃迁的速率。

三能级系统

对于三能级系统，假设$E_1<E_2<E_3$，如果亚稳态$E_2$的寿命足够长，且$E_3$的寿命足够短（快速弛豫到亚稳态），则可以实现粒子数反转。

对于亚稳态：

$$\frac{dN_2}{dt}=-A_{21}N_2-B_{21}\rho(\nu)N_2+B_{32}\rho(\nu)N_3$$

对于抽运高能级：

$$\frac{dN_3}{dt}=-A_{31}N_3-B_{32}\rho(\nu)N_3+B_{13}\rho(\nu)N_1$$

令$B_{32}\gg 1,B_{21}\approx0$，则有：

$$\frac{dN_2}{dt}=-A_{21}N_2+B_{13}\rho(\nu)N_1$$

稳态时：

$$\frac{N_2}{N_1}=\frac{B_{13}\rho(\nu)}{A_{21}}$$

记饱和光强$I_{sat}=A_{21}/B_{13}$，外光强超过饱和光强，即可实现粒子数反转：

$$\frac{N_2}{N_1}=\frac{\rho(\nu)}{I_{sat}}>1$$

三能级系统的粒子数反转是通过快速抽运高能级$E_3$到亚稳态$E_2$实现的。

四能级系统

同样的道理，假设$E_0<E_1<E_2<E_3$：

$$\frac{dN_2}{dt}=-A_{21}N_2+B_{03}\rho(\nu)N_0$$ $$\frac{dN_1}{dt}-A_{10}N_1-B_{10}\rho(\nu)N_1$$

当$B_{10}\gg1$时，$N_1\approx0$，自然实现了粒子数反转。

四能级系统比三能级系统更容易实现粒子数反转，因为$N_1$也被快速抽运至$E_0$。

为什么不选择$N_0$和$N_2$比较呢？这是因为粒子数反转涉及的能级为$E_1$和$E_2$，在四能级系统中，基态出了作为中间态。并不参与激光的跃迁。

激光器的基本结构

激光器的基本结构包括增益介质、泵浦源和谐振腔。

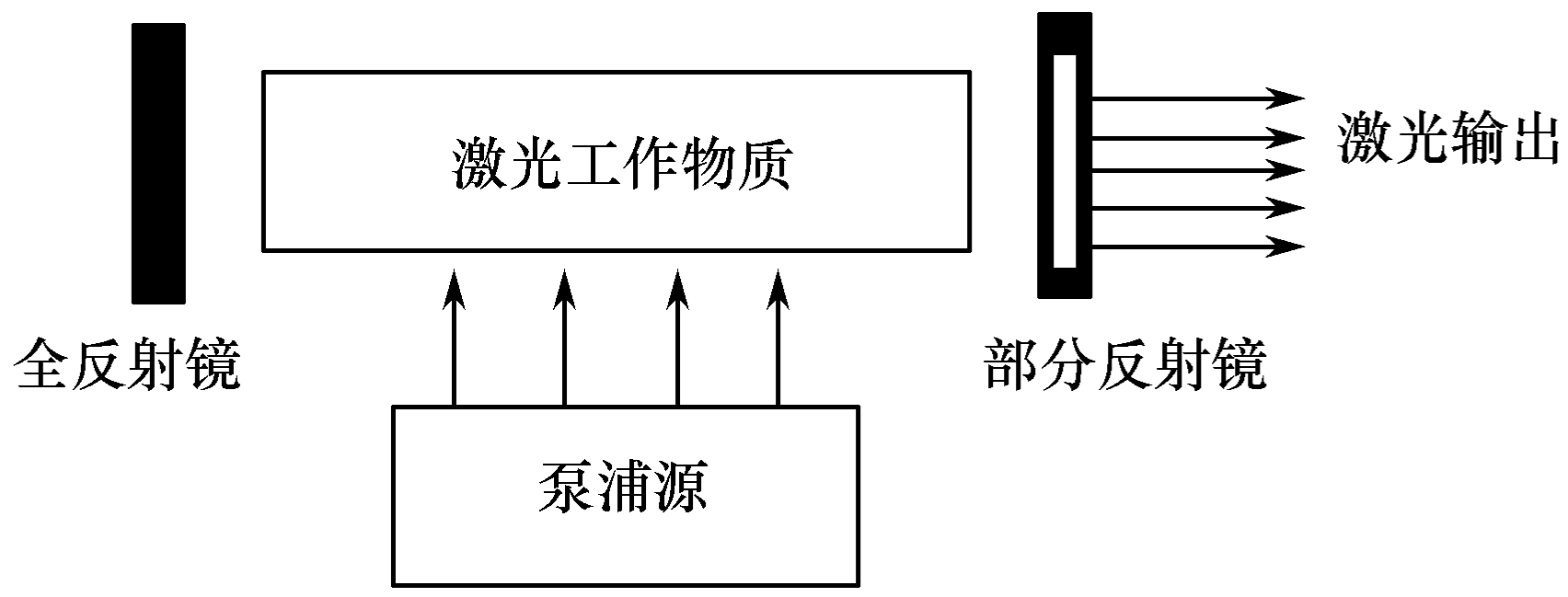
泵浦源：对激光工作物质进行激励，将激活粒子从基态抽运到高能级，以实现粒子数反转。

谐振腔：增加工作介质的有效长度。左边是全反射镜，右边是部分反射镜。全反射镜将光线全部反射回工作介质，部分反射镜则允许一部分光线透出，形成激光输出。

谐振腔除了进行光放大，还可以选择特定方向的光。

工作介质：实现粒子数反转并产生光的受激辐射放大作用的物质体系。激光介质可以是气体、液体、固体和半导体，要求存在亚稳态能级。