以下介绍动力学（含时）模型。

分子马达

分子马达是细胞内负责运输和运动的蛋白质机器。它们通过化学能（通常来自ATP水解）转换为机械能，推动细胞内的物质运输。

分子马达分为以下类型：

线动马达：如肌球蛋白，沿微丝（肌动蛋白）移动，主要负责细胞收缩和物质运输。
转动马达：如噬菌体包装DNA的马达和细菌鞭毛的马达。
聚合马达
易位马达

单态模型

描述分子马达需要区分内部态和外部态，其中内部态指的是马达的构象状态（如活动臂的位置和马达头部和不同分子的结合态），外部态指的是马达的具体位置。

扩散方程

仅考虑马达的外部态，假设其在外力F的作用下分别以速率$k_+(F)$和$k_-(F)$前后运动，其位置概率$p(n,t)$的演化方程为：

$p(n,t+\Delta t) = p(n-1,t)k_+\Delta t + p(n+1,t)k_-\Delta t+p(n,t)(1-k_-\Delta t-k_+\Delta t)$

移项得到差分格式：

$\frac{p(n,t+\Delta t)-p(n,t)}{\Delta t} = k_+ p(n-1,t) - (k_+ + k_-) p(n,t) + k_- p(n+1,t)$

即：

$\frac{\partial p(n,t)}{\partial t} = k_+ p(n-1,t) - (k_+ + k_-) p(n,t) + k_- p(n+1,t)$

将位置概率写为连续变量$p(x,t)$，泰勒展开：

$p(x\pm a,t)\approx p(x,t) \pm a\frac{\partial p}{\partial x} + \frac{a^2}{2}\frac{\partial^2 p}{\partial x^2}$

代入差分方程：

$\begin{aligned} \frac{\partial p(x,t)}{\partial t} &= k_+ p(x-a,t) - (k_+ + k_-) p(x,t) + k_- p(x+a,t)\\ &= k_+ \left(p(x,t) - a\frac{\partial p}{\partial x} + \frac{a^2}{2}\frac{\partial^2 p}{\partial x^2}\right) - (k_+ + k_-) p(x,t) + k_- \left(p(x,t) + a\frac{\partial p}{\partial x} + \frac{a^2}{2}\frac{\partial^2 p}{\partial x^2}\right)\\ &= -(k_+ - k_-) a\frac{\partial p}{\partial x} + \frac{a^2}{2}(k_+ + k_-) \frac{\partial^2 p}{\partial x^2}\\ \end{aligned}$

这是一个有外势场的扩散方程：

$\frac{\partial p(x,t)}{\partial t} = D\frac{\partial^2 p}{\partial x^2} - v\frac{\partial p}{\partial x}$

其中$D = \frac{(k_+ + k_-) a^2}{2}$是扩散系数，$v = (k_+ - k_-) a$是漂移速度。

对于平衡态，马达的速率满足详细平衡条件：

$k_+(F) p(n-1,t) = k_-(F) p(n,t)$

因此：

$\frac{k_+(F=0)}{k_-(F=0)} = \frac{p(n,t)}{p(n-1,t)}= e^{-\beta \Delta G}$

其中，$\Delta G= G(n) - G(n-1)$。有外力的时候，$\Delta G’= G(n) - G(n-1) + F a$，因此：

$\frac{k_+(F)}{k_-(F)} = e^{-\beta \Delta G'} = e^{-\beta (\Delta G+ F a)}$

速率与外力的关系

现在我们只知道$k_+(F)$和$k_-(F)$的比值，假设外力只影响前向速率$k_+(F)$，而后向速率$k_-(F)$不受影响，则有：

$k_+(F) = k_- e^{-\beta(\Delta G+ F a)}$

则步进速率：

$v = (k_+ - k_-) a = k_- a (e^{-\beta(\Delta G+ F a)} - 1)$

反之，如果外力只影响后向速率$k_-(F)$，而前向速率$k_+(F)$不受影响，则有：

$v = (k_+ - k_-) a = k_+ a (1 - e^{-\beta(\Delta G+ F a)})$

通过实验得到，外力其实影响后向速率$k_-(F)$。

速率与ATP浓度的关系

考虑A个ATP、D个ADP和P个磷酸根在$\Omega$个格子中，对于n态，其权重为：

$w_n=\frac{\Omega!}{A!D!P!(\Omega-A-D-P)!}e^{-\beta A\epsilon_{bound}}$

其中$\epsilon_{bound}$是ATP结合能。对于n+1态，其权重为：

$w_{n+1}=\frac{\Omega!}{(A-1)!(D+1)!(P+1)!(\Omega-A-D-P-1)!}e^{-\beta (A-1)\epsilon_{bound}}$

因此，ATP水解自由能的贡献为：

$e^{-\beta\Delta G_{hydrolysis}} = \frac{w_{n+1}}{w_n} = \frac{A}{DP} e^{\beta \epsilon_{bound}}$

如果只有前进速率$k_+$受ATP浓度影响，而后退速率$k_-(F)$不受影响，则有：

$\begin{cases}k_+=\Gamma_+ e^{-\beta(\Delta G_{barrier}+\Delta G_{hydrolysis})}\\ k_-=\Gamma_- e^{-\beta(\Delta G_{barrier})}\end{cases}$

速率为：

$v = (k_+ - k_-) a = a(k_+^0[A] - k_-)$

其中，$k_+^0 = \Gamma_+ e^{-\beta \Delta G_{barrier}}/[A]$，$[A]$是标准ATP浓度。ATP水解促进向前的步进，所以$\Delta G_{hydrolysis}<0$。该模型指出了线性关系，但是ATP浓度饱和时，却没有指出速率的饱和。

如果只有后退速率$k_-(F)$受ATP浓度影响，而前进速率$k_+(F)$不受影响，则有：

$\begin{cases}k_+=\Gamma_+ e^{-\beta(\Delta G_{barrier})}\\ k_-=\Gamma_- e^{-\beta(\Delta G_{barrier}-\Delta G_{hydrolysis})}\end{cases}$

速率为：

$v = (k_+ - k_-) a = a(k_+ - k_-^0[A])$

其中，$k_-^0 = \Gamma_- e^{-\beta \Delta G_{barrier}}/[A]$，$[A]$是标准ATP浓度。该模型指出了非线性关系，并且速率饱和，但是在ATP浓度较低时，速率会急剧下降。

双态模型

假设每个位点上存在两种构象状态：0和1，不同位点的跃迁即为$k_A$，同一位点的跃迁为$k_B$，则演化方程为：

$\frac{dp_0(n,t)}{dt} = k^+_A p_1(n-1,t) +k_B^-p_1(n,t)-k_A^- p_0(n,t) - k_B^+ p_0(n,t)$ $\frac{dp_1(n,t)}{dt} = k^-_A p_0(n+1,t) +k_B^+p_0(n,t)-k_A^+ p_1(n,t) - k_B^- p_1(n,t)$

记所有位点上不同状态的概率和为$P_0$和$P_1$，则有：

$\frac{dP_0}{dt} = k^+_A P_1 +k_B^-P_1-k_A^- P_0 - k_B^+ P_0$ $\frac{dP_1}{dt} = k^-_A P_0+k_B^+P_0-k_A^+ P_1- k_B^- P_1$

稳态时：

$\begin{cases} k^+_A P_1 +k_B^-P_1=k_A^- P_0 + k_B^+ P_0\\ P_0 + P_1 = 1 \end{cases}$

解得：

$P_0 = \frac{k^+_A +k_B^-}{k_A^- + k_B^+ + k^+_A + k_B^-}$ $P_1 = \frac{k_A^- + k_B^+}{k_A^- + k_B^+ + k^+_A + k_B^-}$

设不同状态的距离为$\delta$，不同位点的距离为$a$，速度计算为：

$v=\delta(P_0k_B^+ - P_1 k_B^-)+(a-\delta)(P_1 k_A^- - P_0 k_A^+)=a\frac{k_A^+k_B^- + k_A^-k_B^-}{k_A^- + k_B^+ + k^+_A + k_B^-}$

乌贼的巨型轴突：生物电

能斯特电势

细胞内的大分子主要带负电，如果膜对任何离子都没有通透性，那么膜两边的电位差为0。实际上，内部固定的负电荷会吸引正离子，使得膜内外的离子分布不均匀，形成电位差。

根据玻尔兹曼分布，在膜内外寻找到相应离子的概率为：

$p_{1/2}=\frac{1}{Z}e^{-\beta zeV_{1/2}}$

则浓度比为：

$\frac{C_1}{C_2}=\frac{p_1}{p_2}=e^{-\beta ze\Delta V}$

即可得到能斯特方程：

$\Delta V =\frac{k_BT}{ze}\ln{\frac{c_1}{c_2}}= \frac{RT}{zF} \ln \frac{c_1}{c_2}$

其中$F=N_Ae$是法拉第常数。

由于膜主要对$K^+$通透，因此能斯特电势主要由$K^+$决定。常见离子的膜内外浓度及其能斯特电势如下：

离子	内部浓度 (mM)	外部浓度 (mM)	能斯特电势 (mV)
$K^+$	155	4	-98
$Na^+$	12	145	+67
$Cl^-$	4	120	-90
$Ca^{2+}$	$10^{-4}$	1.5	+130

因此，膜的静息电位和接近于$K^+$的能斯特电势，约为-90mV。注意到$\frac{RT}{F} \approx 25.7$ mV，因此热运动导致的电势差在膜电位中起到了重要作用。

门开关模型

膜通道蛋白的开关和膜内外电势差有关。考虑一个二态模型，其处于开启状态的概率和此前推导的蛋白质双态模型一样：

$p_{open}=\frac{e^{-\beta \Delta G}}{1+e^{-\beta \Delta G} }$

其中$\Delta G $是开启和关闭状态的自由能差。由实验可知，膜通道在内外电势差极大的时候喜好关闭，我们可以用偶极子在电场中的能量来类比：

$\Delta G = \Delta G_{conf}-p\frac{V_{mem}}{d}$

其中，$\Delta G_{conf}$是构象能，$p$是偶极矩，$V_{mem}$是膜电位，$d$是膜的厚度。记：

$V^*=\frac{d\Delta G_{conf}}{p}$

则有：

$p_{open}=\frac{1}{1+\exp{[\beta (V^*-V_{mem})p/d]}}$

去极化

去极化是指膜电位从静息电位（通常为负值）变为更接近零或正值的过程，从而产生动作电位。去极化通常是由于膜通道的开放，允许正离子（如$Na^+$）进入细胞，导致膜内外电位差减小。

每次去极化的过程中转移的电荷对胞内离子浓度的扰动非常小。根据平行板电容器的公式：

$C/A=\frac{\varepsilon}{d}\approx 0.7\mu F/cm^2(d\approx 3nm)$

可以计算出每次去极化的电荷量：

$Q/V=C\Delta V /L\approx 0.7\mu F/cm^2 \times 100mV/20\mu m = 3.5\times 10^4nC/cm^3$

与此同时，细胞内离子的浓度为：

$Q/V=100\text{mmol/L}\times 6.02\times 10^{23}mol^{-1}\times 1.6\times 10^{-10}nC/mol\approx 1.0\times 10^{10}nC/cm^3$

去极化的电荷转移形成跨膜离子流，其正比于两端的化学势差和膜的电导率：

$I = g(\frac{k_BT}{ze}\ln{\frac{c_1}{c_2}} +V_{in}-V_{out})= g(V_{mem}-V_{Nernst})$

然而实际上的电流并非与电压线性相关，这启发我们固定与电导的线性关系，转而研究电导本身和门开关模型的关系。假设电导和通道开启的概率成正比，在超过阈值电压$V^*$时产生非线性跃变，即可解释膜电流的非线性特性。

带门开关的去极化模型

膜电位的微分方程为：

$C\frac{dV_{mem}}{dt} = g_K(V^K_{Nernst} - V_{mem}) + g_{Na}(V^{Na}_{Nernst} - V_{mem})$

可得稳定解：

$V_{mem} = \frac{g_K V^K_{Nernst} + g_{Na} V^{Na}_{Nernst}}{g_K + g_{Na}}$

我们作出以下假设：$g_K$对膜电位不敏感（其响应时间为5ms），而$g_{Na}$对膜电位敏感（其响应时间为1ms）：

$g_{Na} = g_{Na}^{open}\frac{1}{1+\exp{[\beta (V^* - V_{mem})p/d]}}$

则有：

当$V_{mem} < V^*$时，$g_{Na}$接近0，膜电位接近$V^K_{Nernst}$；
当$V_{mem} > V^*$时，$g_{Na}$接近$g_{Na}^{open}$，膜电位接近$V^{Na}_{Nernst}$。

电报方程

由数学物理方程中的典型波动方程可知，电报方程是描述电信号传播的偏微分方程：

$\frac{\partial^2 V}{\partial x^2}=LC\frac{\partial^2 V}{\partial t^2} + (RC+GL)\frac{\partial V}{\partial t}+RGV$

细胞电路中不存在电感$L$，因此电报方程简化为：

$\frac{\partial^2 V}{\partial x^2} = RC\frac{\partial V}{\partial t} + RGV$

其中，$RC$的单位是$[\Omega] [F]/[m]^2=[s]/[m]^2$，重新改写为以下膜电位传导的形式：

$\lambda^2 \frac{\partial^2 V}{\partial x^2} = \tau\frac{\partial V}{\partial t} +\frac{g_{Na}(V)}{g_K}[V-V_{Nernst}^{Na}]+[V-V_{Nernst}^{K}]$

其中，$\lambda$是膜电位的特征传播长度，$\tau$是膜电位的特征衰减时间。

通过数值求解，可以解出类似波传导的形式，且发现$v\propto \sqrt{d}$，这解释为什么乌贼的神经轴突很粗。

alt

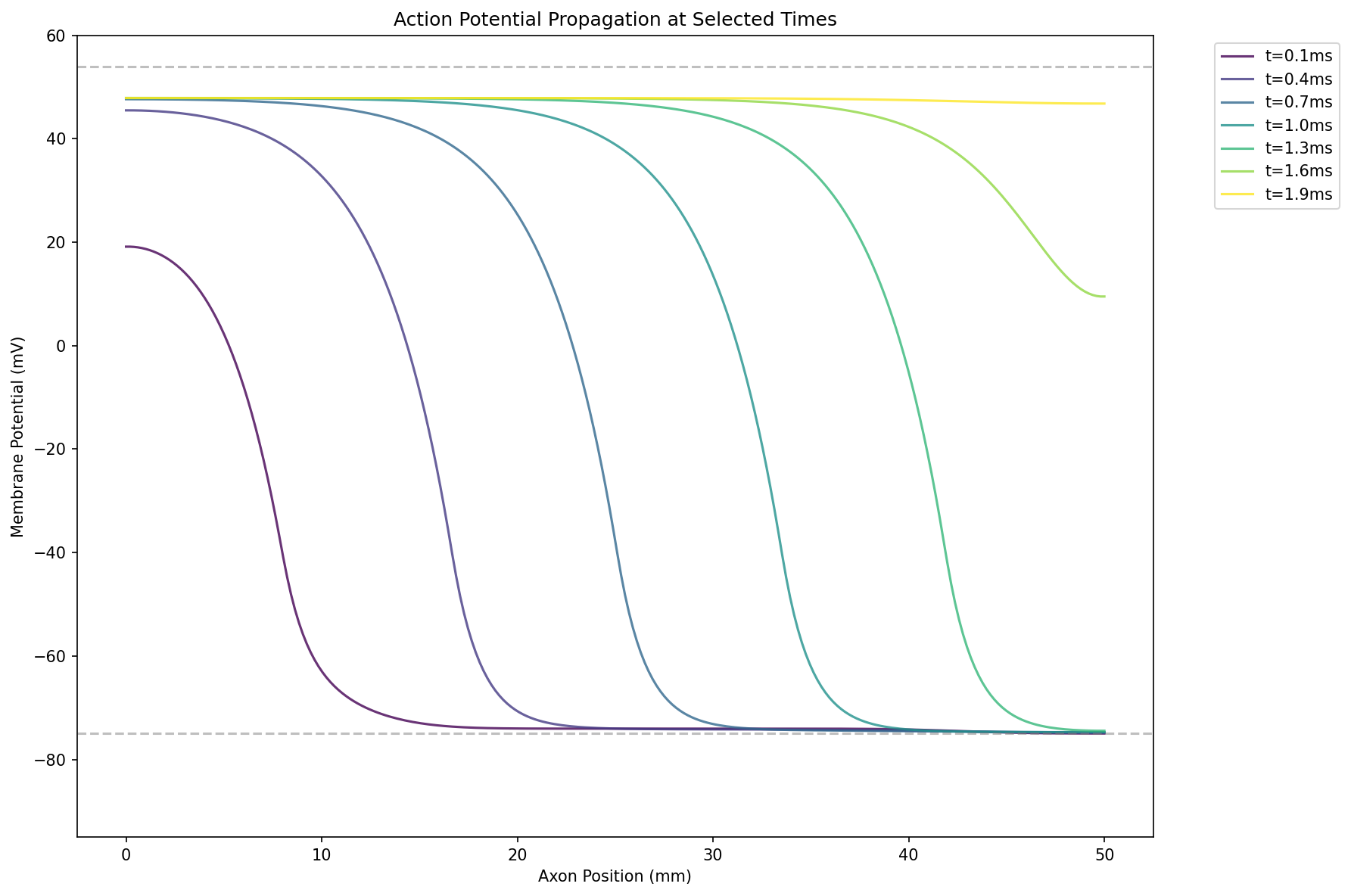
如果刺激很小，则膜电位近似指数衰减，不会产生动作电位：

alt

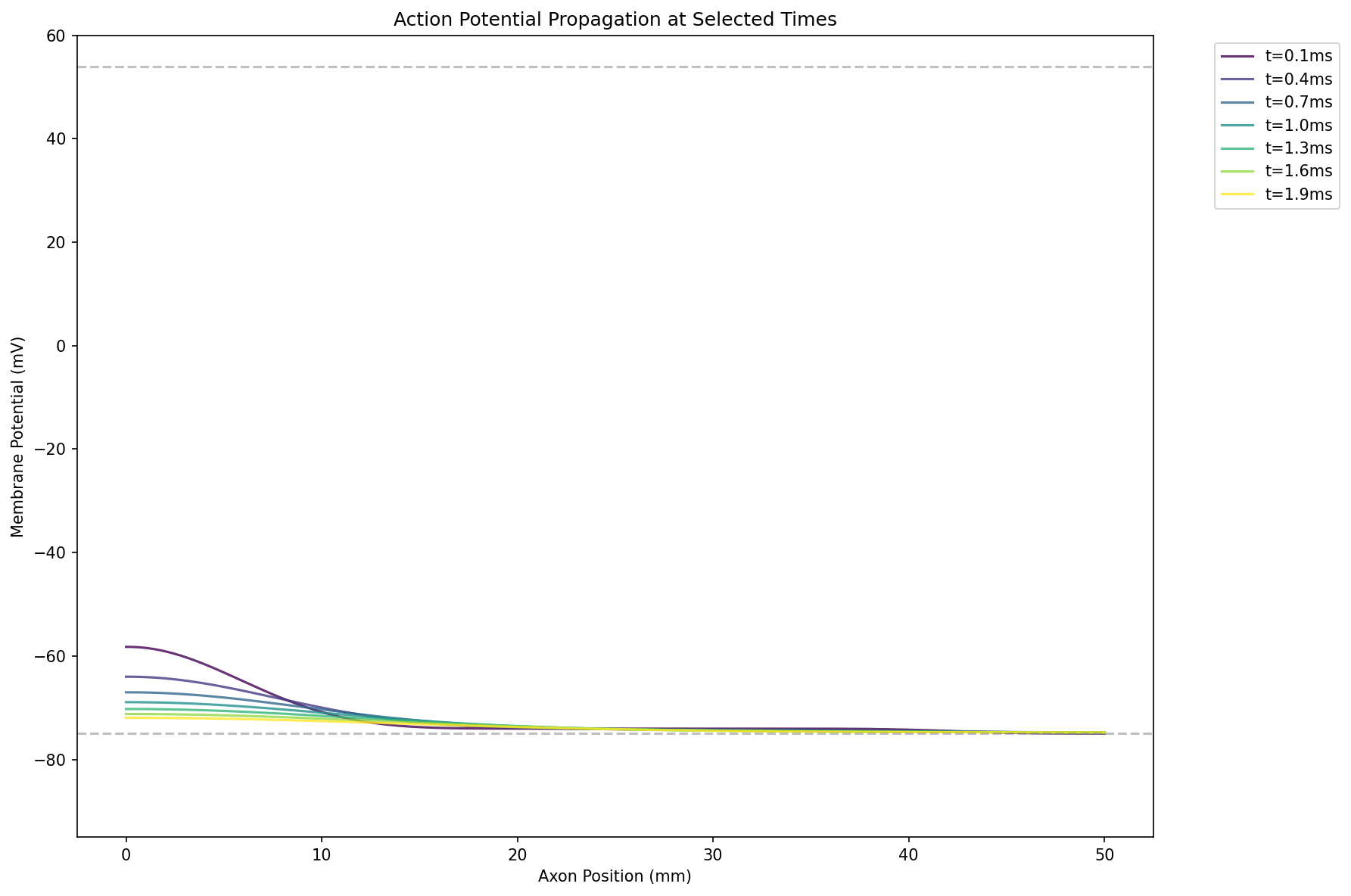
然而，目前的模型解出的波函数不能回到静息电位。这启发我们除了开启和关闭通道外，还需要考虑通道的失活。失活是指通道在开启后不久就会自动关闭，导致无法持续导电。

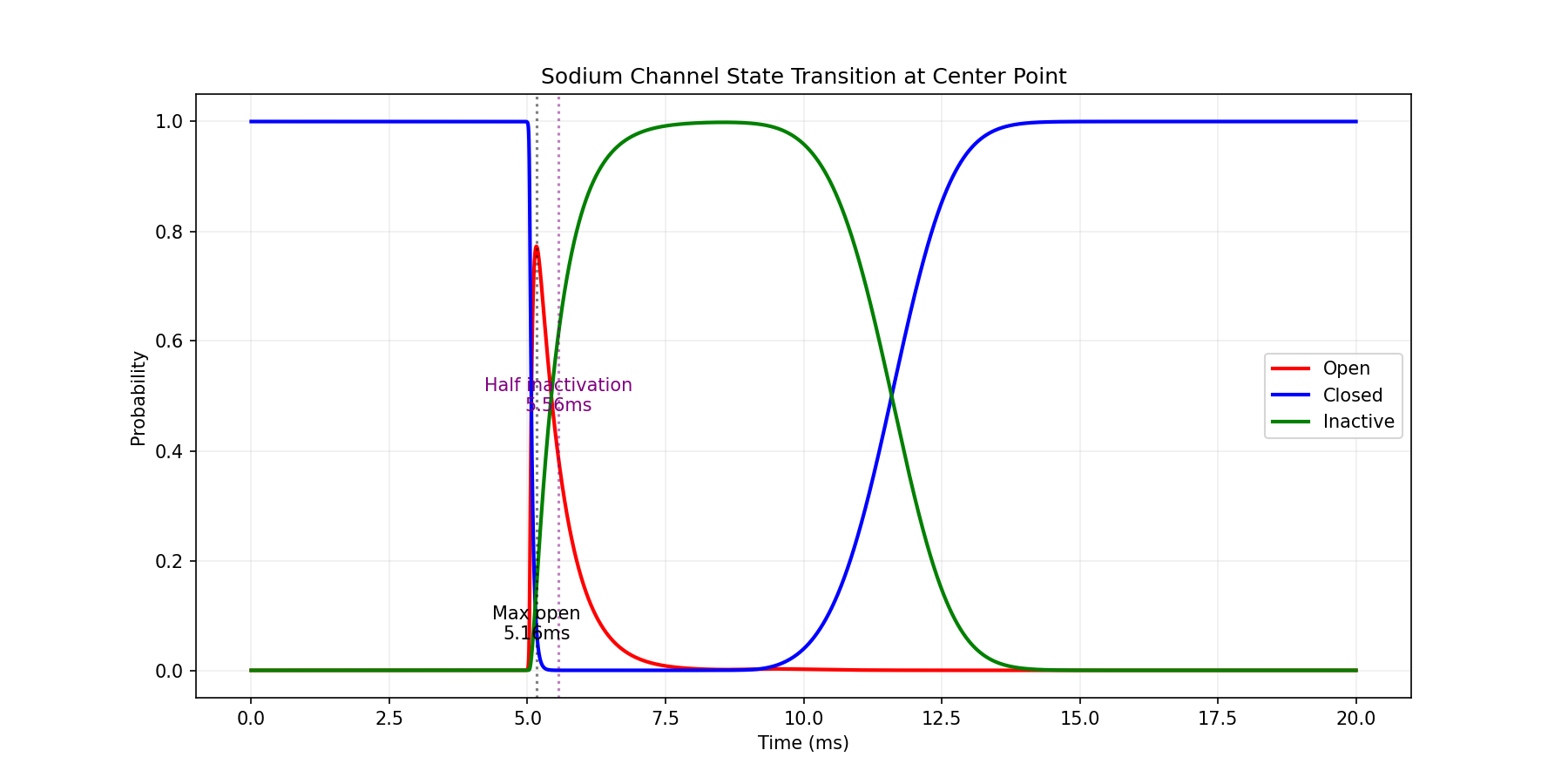
钠离子通道失活

假设存在以下状态间的转换：

$\text{closed}~\underset{k_{close}}{\overset{k_{open}}{\rightleftharpoons}}~ \text{open}\underset{k_{open}}{\overset{k_{inact}}{\rightleftharpoons}} \text{inactive}$

进行以下简化：

$\text{closed} \xrightarrow{k_{open}} \text{open} \xrightarrow{k_{inact}} \text{inactive}$

重新定义$g_{Na}$：

$g_{Na} = g_{Na}^{open} p_{open}+ g_{Na}^{closed} p_{closed}\approx g_{Na}^{open} p_{open}$

乍一看，这和上述模型相同，不过，现在的$p_{open}$是一个三态模型的概率：

$\begin{cases} \frac{dp_{closed}}{dt} = -k_{open} p_{closed}\\ \frac{dp_{open}}{dt} = k_{open} p_{closed} - k_{inact} p_{open}\\ \frac{dp_{inactive}}{dt} = k_{inact} p_{open} \end{cases}$

其中，通道开启速率与膜电位有关：

$k_{open} = k_{open}^{max} \frac{1}{1+\exp{[\beta (V^* - V_{mem})p/d]}}$

这就做到了动作电位产生后，通道会迅速失活，导致膜电位回到静息状态。

alt

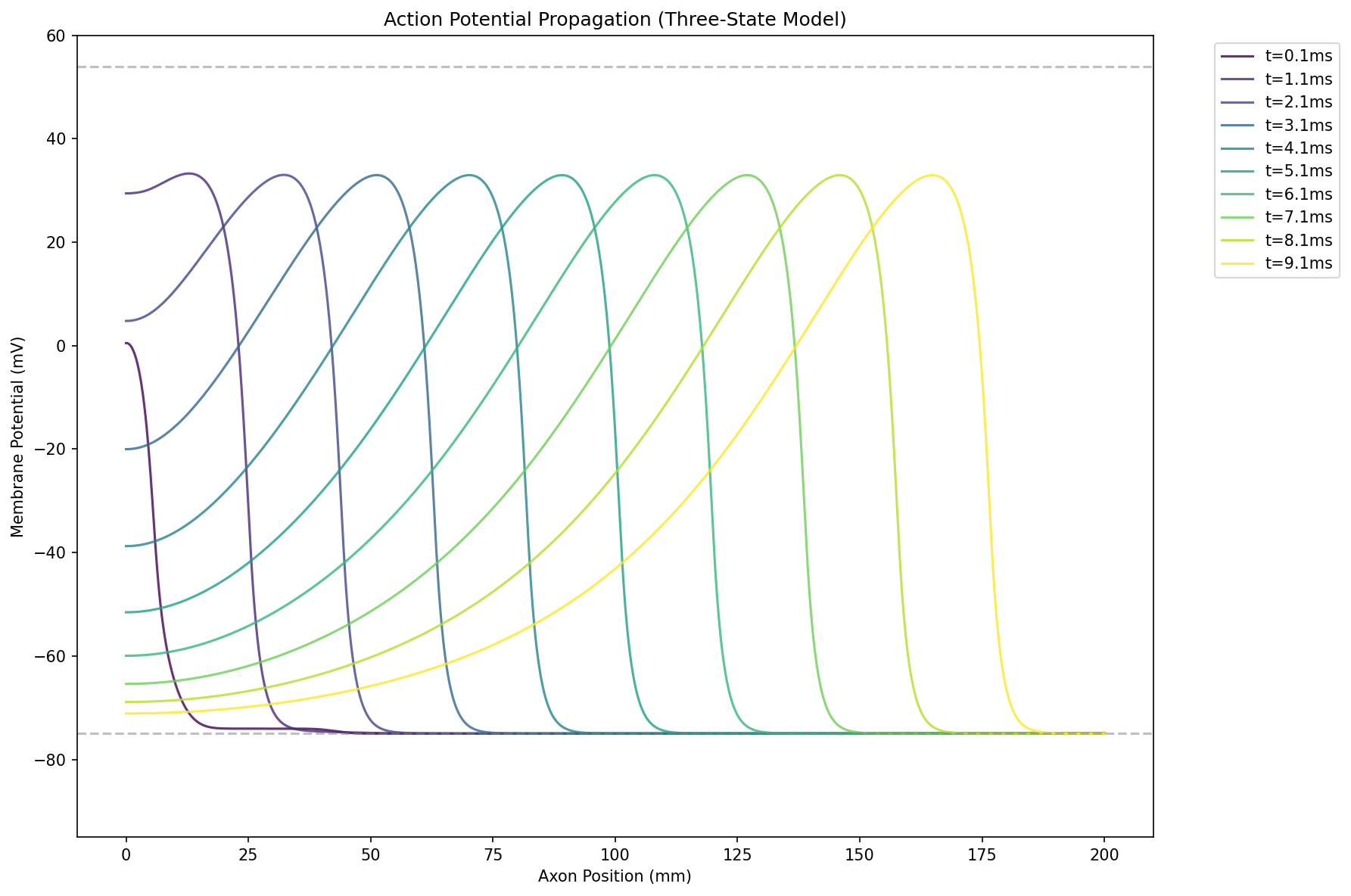
失活蛋白的回正

在原来的基础上作出以上修正：

$\begin{cases} \frac{dp_{closed}}{dt} = -k_{open} p_{closed}+k_{close} p_{inactive}\\ \frac{dp_{open}}{dt} = k_{open} p_{closed} - k_{inact} p_{open}\\ \frac{dp_{inactive}}{dt} = k_{inact} p_{open}-k_{close} p_{inactive} \end{cases}$

即可得到失活蛋白向关闭蛋白的转变（这里面需要类似门开关的机制）：

alt