拉格朗日动力学

拉格朗日方程

拉格朗日关系

将真实坐标用广义坐标表示：

$$\vec{r}_i = \vec{r}_i(q_1, q_2, \cdots, q_{N-k}, t)$$ $$\dot{\vec{r}}_i = \sum_{\alpha=1}^{N-k}\frac{\partial \vec{r}_i}{\partial q_\alpha}\dot{q}_\alpha + \frac{\partial \vec{r}_i}{\partial t}$$

分别对$\dot{q}_\beta$和$q_\beta$求导：

$$\begin{aligned} \frac{\partial \dot{\vec{r}}_i}{\partial \dot{q}_\beta} &= \frac{\partial}{\partial \dot{q}_\beta}\left(\sum_{\alpha=1}^{N-k}\frac{\partial \vec{r}_i}{\partial q_\alpha}\dot{q}_\alpha + \frac{\partial \vec{r}_i}{\partial t}\right)\\ &= \frac{\partial \vec{r}_i}{\partial q_\beta}\\ \frac{\partial \dot{\vec{r}}_i}{\partial q_\beta} &= \frac{\partial}{\partial q_\beta}\left(\sum_{\alpha=1}^{N-k}\frac{\partial \vec{r}_i}{\partial q_\alpha}\dot{q}_\alpha + \frac{\partial \vec{r}_i}{\partial t}\right)\\ &= \sum_{\alpha=1}^{N-k}\frac{\partial^2 \vec{r}_i}{\partial q_\beta\partial q_\alpha}\dot{q}_\alpha + \frac{\partial^2 \vec{r}_i}{\partial q_\beta\partial t}\\ &=\frac{\partial }{\partial t}\left(\frac{\partial \vec{r}_i}{\partial q_\beta}\right) + \frac{\partial }{\partial q_\alpha}\sum_{\alpha=1}^{N-k}\frac{\partial \vec{r}_i}{\partial q_\beta}\dot{q}_\alpha\\ &=\frac{d}{dt}\left(\frac{\partial \vec{r}_i}{\partial q_\beta}\right) \end{aligned}$$

拉格朗日方程的推导

广义坐标的达朗贝尔原理：

$$\sum_{j=1}^{N-k} \left(Q_j - \sum_{i=1}^n m_i\ddot{\vec{r}}_i\cdot\frac{\partial \vec{r}_i}{\partial q_j}\right)\delta q_j = 0$$

将拉格朗日关系代入，计算惯性力的部分：

$$\begin{aligned} \sum_{i=1}^n m_i\ddot{\vec{r}}_i\cdot\frac{\partial \vec{r}_i}{\partial q_j} &=\sum_{i=1}^n m_i\frac{d\dot{\vec{r}}_i}{dt}\cdot\frac{\partial \vec{r}_i}{\partial q_j}\\ &=\sum_{i=1}^n m_i\frac{d}{dt}\left(\dot{\vec{r}}_i\cdot\frac{\partial \vec{r}_i}{\partial q_j}\right)-\sum_{i=1}^n m_i\left(\dot{\vec{r}}_i\cdot\frac{d}{dt}\frac{\partial \vec{r}_i}{\partial q_j}\right)\\ &=\sum_{i=1}^n m_i\frac{d}{dt}\left(\dot{\vec{r}}_i\cdot\frac{\partial \dot{\vec{r}}_i}{\partial \dot{q}_j}\right)-\sum_{i=1}^n m_i\left(\dot{\vec{r}}_i\cdot\frac{\partial \dot{\vec{r}}_i}{\partial q_j}\right)\\ &=\frac{d}{dt}\frac{\partial }{\partial \dot{q}_j}\left(\sum_{i=1}^n\frac12m_i |\dot{\vec{r}}_i|^2\right)-\frac{\partial }{\partial q_j}\left(\sum_{i=1}^n\frac12m_i |\dot{\vec{r}}_i|^2\right)\\ &=\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_j}-\frac{\partial T}{\partial q_j}\\ \end{aligned}$$

也就是说：

$$Q_j=\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_j}-\frac{\partial T}{\partial q_j}$$

这就是欧拉-拉格朗日方程。如果广义力是保守力，则可以引入广义势能$V$，使得：

$$Q_j = -\frac{\partial V}{\partial q_j}$$

将其代入拉格朗日方程：

$$\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_j}-\frac{\partial L}{\partial q_j}= 0,L=T-V$$

从量纲上判断，$\frac{\partial L}{\partial \dot{q}_j}$是动量量纲，$\frac{\partial L}{\partial q_j}$是力量纲，这个方程的地位有点像牛顿第二定律$F=\frac{d}{dt}p$。这点在下面也会谈到。

如果你对变分原理熟悉，可以看出这其实是哈密顿作用量取极值的结果：

$$\delta S = \delta \int_{t_1}^{t_2} L(q,q';t) dt = 0$$

对于这样一个泛函，极值的条件为：

$$\frac{\partial L}{\partial q} - \frac{d}{dt}\frac{\partial L}{\partial q'} = 0$$

和上面的结果是一样的。

对于自由粒子，其拉格朗日量为$L=\frac12 m v^2$，则有：

$$ma = 0$$

对于保守系统，其拉格朗日量为$L=T-V$，则有：

$$ma= -\nabla V$$

双摆的拉格朗日方程

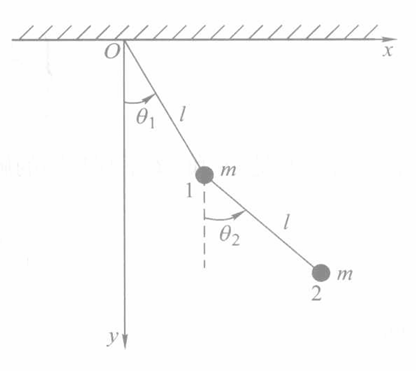
考虑双摆的广义坐标为$(\theta_1,\theta_2)$，对应的摆长为$l_1,l_2$，质量为$m_1,m_2$，真实坐标为$(x_1,y_1,x_2,y_2)$，则有：

$$\begin{aligned} x_1 &= l_1\sin\theta_1\\ y_1 &= -l_1\cos\theta_1\\ x_2 &= l_1\sin\theta_1 + l_2\sin\theta_2\\ y_2 &= -l_1\cos\theta_1 - l_2\cos\theta_2 \end{aligned}$$

则有：

$$\begin{aligned} \dot{x}_1 &= l_1\cos\theta_1\dot{\theta}_1\\ \dot{y}_1 &= l_1\sin\theta_1\dot{\theta}_1\\ \dot{x}_2 &= l_1\cos\theta_1\dot{\theta}_1 + l_2\cos\theta_2\dot{\theta}_2\\ \dot{y}_2 &= l_1\sin\theta_1\dot{\theta}_1 + l_2\sin\theta_2\dot{\theta}_2 \end{aligned}$$

动能写作：

$$\begin{aligned} T &= \frac12 m_1(\dot{x}_1^2 + \dot{y}_1^2) + \frac12 m_2(\dot{x}_2^2 + \dot{y}_2^2)\\ &= \frac12 m_1\left(l_1^2\cos^2\theta_1\dot{\theta}_1^2 + l_1^2\sin^2\theta_1\dot{\theta}_1^2\right) + \frac12 m_2\left((l_1\cos\theta_1\dot{\theta}_1 + l_2\cos\theta_2\dot{\theta}_2)^2 + (l_1\sin\theta_1\dot{\theta}_1 + l_2\sin\theta_2\dot{\theta}_2)^2\right)\\ &=\frac12(m_1+m_2)l_1^2\dot{\theta}_1^2 + m_2 l_1 l_2 \dot{\theta}_1 \dot{\theta}_2 \cos(\theta_1 - \theta_2) + \frac12 m_2 l_2^2 \dot{\theta}_2^2 \end{aligned}$$

势能写作：

$$\begin{aligned} V &= m_1 g y_1 + m_2 g y_2\\ &= -m_1 g l_1\cos\theta_1 - m_2 g (l_1\cos\theta_1 + l_2\cos\theta_2)\\ &= -m_1 g l_1\cos\theta_1 - m_2 g l_1\cos\theta_1 - m_2 g l_2\cos\theta_2\\ &= - (m_1 + m_2) g l_1\cos\theta_1 - m_2 g l_2\cos\theta_2 \end{aligned}$$

拉格朗日方程解为：

$$\begin{aligned} \text{Left}&= \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}_1}\\ &= (m_1 + m_2) l_1^2 \ddot{\theta}_1 + m_2 l_1 l_2 \frac{d}{dt} \dot{\theta}_2\cos(\theta_1 - \theta_2)\\ &= (m_1 + m_2) l_1^2 \ddot{\theta}_1 + m_2 l_1 l_2 \ddot{\theta}_2\cos(\theta_1 - \theta_2)- m_2 l_1 l_2 \dot{\theta}_2\sin(\theta_1 - \theta_2)(\dot{\theta_1}-\dot{\theta_2})\\ \text{Right}&= \frac{\partial L}{\partial \theta_1}\\ &= -m_2 l_1 l_2 \dot{\theta}_1 \dot{\theta}_2 \sin(\theta_1 - \theta_2) -(m_1 + m_2) g l_1 \sin\theta_1 \\ \end{aligned}$$

化简得到：

$$(m_1 + m_2) l_1 \ddot{\theta}_1 + m_2 l_2 \ddot{\theta}_2\cos(\theta_1 - \theta_2)+ m_2 l_2 \dot{\theta}_2^2\sin(\theta_1 - \theta_2)+(m_1 + m_2) g \sin\theta_1=0$$

对于$\theta_2$，可以得到另一个式子：

$$m_2 l_2\ddot{\theta}_2 + m_2 l_1 \ddot{\theta}_1\cos(\theta_1 - \theta_2) - m_2 l_1\dot{\theta}_1^2\sin(\theta_1 - \theta_2) +m_2g\sin\theta_2 = 0$$

对称性和守恒量

广义动量守恒

定义广义动量为：

$$p_j = \frac{\partial L}{\partial \dot{q}_j}$$

如果拉格朗日量中的势能不依赖于广义速度，则有：

$$p_j = \frac{\partial T}{\partial \dot{q}_j}$$

如果：

$$\frac{d}{dt}\frac{\partial L}{\partial \dot{q_j}} = 0$$

则可以积分出：

$$p_j =\frac{\partial L}{\partial \dot{q}_j} = C_j$$

其中$C_j$为常数。这个常数就是广义动量守恒量。

广义能量守恒

对拉格朗日函数求时间微分：

$$\begin{aligned} \frac{dL}{dt} &= \sum_{j=1}^{N-k}\left(\frac{\partial L}{\partial q_j}\dot{q}_j + \frac{\partial L}{\partial \dot{q}_j}\ddot{q}_j\right) + \frac{\partial L}{\partial t}\\ &=\sum_{j=1}^{N-k}\left[\left(\frac{d}{dt}\frac{\partial L}{\partial \dot{q_j}}\right)\dot{q}_j + \frac{\partial L}{\partial \dot{q}_j}\frac{d}{dt}\dot{q}_j\right] + \frac{\partial L}{\partial t}\\ &=\sum_{j=1}^{N-k}\left[\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_j}\dot{q}_j\right)\right] + \frac{\partial L}{\partial t}\\ \end{aligned}$$

如果拉格朗日量不显含时间，则有：

$$\frac{dL}{dt} - \sum_{j=1}^{N-k}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_j}\dot{q}_j\right)=0$$

这同样是一个守恒量。定义广义能量为：

$$H = \sum_{j=1}^{N-k}\frac{\partial L}{\partial \dot{q}_j}\dot{q}_j - L= \sum_{j=1}^{N-k}p_j\dot{q}_j - L$$

则有：

$$\frac{dL}{dt} = -\frac{dH}{dt}$$

这样或许能回答“拉格朗日函数$L=T-V$的物理意义是什么”了。可以观察到代入$p=mv$后，广义能量函数就是：

$$H=2T-(T-V)=T+V$$

诺特定理

诺特定理指出，连续对称性和守恒定律的一一对应。

• 如果拉格朗日量对某个广义坐标$q_j$不显含，则对应的广义动量$p_j$守恒；
• 如果拉格朗日量对时间不显含，则对应的广义能量$H$守恒。

具体的数学证明过于繁琐，这里不再赘述。