固定坐标系下的质点运动学

矢量力学通过科学抽象，将研究对象简化为刚体乃至质点。我们通过矢量来描述质点的诸多物理量：

选定参考系的原点，质点的位置由径向矢量 $\vec{r}=r\vec{\tau}$ 表示；
质点的运动通过径向矢量的变化——位移来表示：$\Delta \vec{r}=\vec{r}_2-\vec{r}_1$；
质点的平均速度由位移对时间的导数来表示：$\bar{\vec{v}}=\frac{\Delta \vec{r}}{\Delta t}$；
质点的平均加速度由速度对时间的导数来表示：$\bar{\vec{a}}=\frac{\Delta \vec{v}}{\Delta t}$。

很多时候，我们更关心质点的瞬时速度和瞬时加速度：

$\begin{aligned} \vec{v}&=\lim_{\Delta t \to 0} \frac{\Delta \vec{r}}{\Delta t}=\frac{d\vec{r}}{dt}=\dot{r}\vec{\tau}+r\dot{\vec{\tau}}\\ \vec{a}&=\lim_{\Delta t \to 0} \frac{\Delta \vec{v}}{\Delta t}=\frac{d\vec{v}}{dt}=\ddot{r}\vec{\tau}+2\dot{r}\dot{\vec{\tau}}+r\ddot{\vec{\tau}}\\ \end{aligned}$

代入$\dot{\vec{\tau}}=\dot{\theta}\vec{n},\dot{\vec{n}}=-\dot{\theta}\vec{\tau}$，其中$\vec{n}$为单位法向量：

$\begin{aligned} \vec{v}&=\dot{r}\vec{\tau}+r\dot{\theta}\vec{n}\\ \vec{a}&=\ddot{r}\vec{\tau}+2\dot{r}\dot{\theta}\vec{n}+r\ddot{\theta}\vec{n}-r\dot{\theta}^2\vec{\tau}\\ \end{aligned}$

如果我们不展开$\vec{v}$，可以得到：
$\begin{aligned} \vec{a}&=\dot{v}\vec{\tau}+v\dot{\theta}\dot{\vec{n}}\\ &=\dot{v}\vec{\tau}+v\frac{d\theta}{ds}\frac{ds}{dt}\dot{\vec{n}}\\ &=\dot{v}\vec{\tau}+v^2\rho\dot{\vec{n}}\\ \end{aligned}$
其中$\rho$为曲率。

一般我们会在具体的坐标系下进行计算，具体的坐标系会影响基矢的选取。

直角坐标系

在直角坐标系中：

$\begin{aligned} \vec{r}&=x\hat{i}+y\hat{j}+z\hat{k}\\ \vec{v}&=\dot{x}\hat{i}+\dot{y}\hat{j}+\dot{z}\hat{k}\\ \vec{a}&=\ddot{x}\hat{i}+\ddot{y}\hat{j}+\ddot{z}\hat{k}\\ \end{aligned}$

极坐标系

在极坐标系中：

$\begin{aligned} \vec{r}&=r\hat{\tau}\\ \vec{v}&=\dot{r}\hat{\tau}+r\dot{\theta}\hat{n}\\ \vec{a}&=\ddot{r}\hat{\tau}+2\dot{r}\dot{\theta}\hat{n}+r\ddot{\theta}\hat{n}-r\dot{\theta}^2\hat{\tau}\\ \end{aligned}$

其中，速度分为径向速度$\dot{r}$和切向速度$r\dot{\theta}$，加速度分为径向加速度$\ddot{r}-r\dot{\theta}^2$和切向加速度$r\ddot{\theta}+2\dot{r}\dot{\theta}$。其中径向加速度包括：

径向速度的大小变化：$\ddot{r}$；
向心加速度（横向速度的方向变化）：$-r\dot{\theta}^2$。

切向加速度包括：

横向速度的大小变化：$r\ddot{\theta}$；
径向速度的方向变化：$2\dot{r}\dot{\theta}$。

柱坐标系

在柱坐标系中：

$\begin{aligned} \vec{r}&=r\hat{\tau}+z\hat{k}\\ \vec{v}&=\dot{r}\hat{\tau}+r\dot{\theta}\hat{n}+\dot{z}\hat{k}\\ \vec{a}&=\ddot{r}\hat{\tau}+2\dot{r}\dot{\theta}\hat{n}+r\ddot{\theta}\hat{n}-r\dot{\theta}^2\hat{\tau}+\ddot{z}\hat{k}\\ \end{aligned}$

球坐标系

在球坐标系中：

$\begin{aligned} \vec{r}&=r\hat{\tau}\\ \vec{v}&=\dot{r}\hat{\tau}+r\dot{\theta}\hat{\theta}+r\dot{\phi}\sin\theta\hat{\phi}\\ \vec{a}&=(\ddot{r}-r\dot{\theta}^2-r\dot{\phi}^2\sin^2\theta)\hat{\tau}\\&+(2\dot{r}\dot{\theta}+r\ddot{\theta}-r\dot{\phi}^2\sin\theta\cos\theta)\hat{\theta}\\&+(r\ddot{\phi}\sin\theta+2\dot{r}\dot{\phi}\sin\theta+2r\dot{\theta}\dot{\phi}\cos\theta)\hat{\phi}\\ \end{aligned}$

推导该表达式，最关键是推导基矢的导数：一方面可以通过图像直接得出，另一方面可以通过在直角坐标系下表达，然后求导后反代。

另一种方法是通过拉格朗日方程：
$\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}})=\frac{\partial L}{\partial q},[L=\frac12m(\dot{r}^2+r^2\dot{\theta}^2+r^2\sin\theta^2\dot{\phi}^2)-V]$
来推出：
$\begin{aligned}\begin{cases}\dfrac{d}{dt}\left(\dfrac{\partial L}{\partial \dot{r}}\right)&=m\ddot{r}\\\left(\dfrac{\partial L}{\partial {r}}\right)&=mr(\dot{\theta}^2+\sin\theta^2\dot{\phi}^2)-\dfrac{\partial V}{\partial r}\end{cases}\\\Rightarrow \frac{\partial V}{\partial r}=a_r=m(\ddot{r}-r\dot{\theta}^2-r\sin\theta^2\dot{\phi}^2)\end{aligned}$

相对运动

描述运动的时候总会选择一个方便的参考系，但是到了求解具体问题的时候，根据问题选择的参考系显然更简便，这就需要不同参考系之间的互相转换。

已知质点相对于运动参考系$S’$的位置$\vec{r}’$、速度$\vec{v}’$、加速度$\vec{a}’$。另一个的参考系$S$相对于运动参考系的位置、速度、加速度分别为$\vec{R}$、$\vec{V}$、$\vec{A}$，当我们站在这个参考系内，我们认为这个参考系是固定的，这样会方便我们对问题的建模。

任意平动参考系

在新参考系的表示为：

$\begin{cases} \vec{r}(t)&=\vec{r}'+\vec{R}(t)\\ \vec{v}(t)&=\vec{v}'+\vec{V}(t)\\ \vec{a}(t)&=\vec{a}'+\vec{A}(t) \end{cases}$

在不涉及转动（即基矢变化）的新坐标系中，我们发现所有物理量都可以做简单平移来转化得到新的坐标系下的物理量。

旋转参考系

取时间$t=0$的时候两个坐标系基矢重合，则该时间零点瞬间，新坐标系下的物理量表达为：

$\begin{cases} \vec{r}&=\vec{r}'+\vec{\omega}\times\vec{r}dt\approx \vec{r}\\ \vec{v}&=\vec{v}'+\vec{\omega}\times\vec{r}\\ \vec{a}&=\vec{a}'+\vec{\beta}\times\vec{r}+2\vec{\omega}\times\vec{v}'+\vec{\omega}\times(\vec{\omega}\times\vec{r})\\ \end{cases}$

这里不区分两个坐标系下的位置矢量，因为在$t=0$时刻两个坐标系的原点重合，所以位置矢量相同。

这里给出证明：

$\begin{aligned} \vec{a}(t)&=\frac{d\vec{v}(t)}{dt}\\ &=\frac{d}{dt}(\vec{v}'+\vec{\omega}\times\vec{r})\\ &=\frac{d}{dt}\sum(v_i\vec{i}'+\epsilon_{ijk}\omega_i r_j\vec{k}')\\ &=\sum[(a_i'\vec{i}'+v_i'\vec{\omega}\times\vec{i}')+(\epsilon_{ijk}\beta_i r_j\vec{k}'+\epsilon_{ijk}\omega_i v_j'\vec{k}'+\epsilon_{ijk}\omega_i r_j\vec{\omega}\times\vec{k}')]\\ &=\vec{a}'+\vec{\beta}\times\vec{r}+2\vec{\omega}\times\vec{v}'+\vec{\omega}\times(\vec{\omega}\times\vec{r})\\ \end{aligned}$

这里也有更优美的证明。利用以下结论：
$(\frac{d}{dt}\vec{A})_{Still}=(\frac{d}{dt}\vec{A})_{Rotating}+\vec{\omega}\times\vec{A}$
可以得到：
$\begin{aligned} \vec{v}&=\frac{d\vec{r}}{dt}\\ &=\vec{v}'+\vec{\omega}\times\vec{r} \end{aligned}$ $\begin{aligned} \vec{\beta}&=\frac{d\vec{\omega}}{dt}\\ &=\frac{d}{dt}\vec{\omega}'+\vec{\omega}\times\vec{\omega}\\ &=\vec{\beta}' \end{aligned}$
代入下式：
$\begin{aligned} \vec{a}&=\frac{d\vec{v}}{dt}\\ &=\frac{d}{dt}(\vec{v}'+\vec{\omega}\times\vec{r})+\vec{\omega}\times(\vec{v}'+\vec{\omega}\times\vec{r})\\ &=\vec{a}'+\vec{\beta}'\times\vec{r}+2\vec{\omega}\times\vec{v}'+\vec{\omega}\times(\vec{\omega}\times\vec{r})\\ \end{aligned}$

三项牵连加速度，分别是：

$\vec{\beta}\times\vec{r}$：由于参考系的旋转加速度引起的加速度（角加速度）；
$2\vec{\omega}\times\vec{v}’$：由于相对参考系的运动引起的加速度（科里奥利加速度）；
$\vec{\omega}\times(\vec{\omega}\times\vec{r})$：由于参考系的旋转引起的加速度（向心加速度）。

实际上应用的时候，是因为我们想计算非惯性系中的加速度才使用相对运动理论，所以不知道的一般是$\vec{a}’$，这说明我们要把上式移项变成：

$\vec{a}'=\vec{a}-\vec{\beta}\times\vec{r}-2\vec{\omega}\times\vec{v}'-\vec{\omega}\times(\vec{\omega}\times\vec{r})$

例子：一个质点做匀速圆周运动，如果在相对静止参考系（即同样转速的旋转参考系）下观察：
$\vec{a}=-\omega v,\quad -2\vec{\omega}\times\vec{v}'=0,\quad -\vec{\omega}\times(\vec{\omega}\times\vec{r})=\omega v$
所以能观察到物体静止。如果是一个质点本身静止，但是我在旋转参考系中观察，物体的加速度为：
$\vec{a}=0,\quad -2\vec{\omega}\times\vec{v}'=-2\omega v,\quad -\vec{\omega}\times(\vec{\omega}\times\vec{r})=\omega v$
所以在旋转参考系中观察到物体正常旋转，有向心加速度。

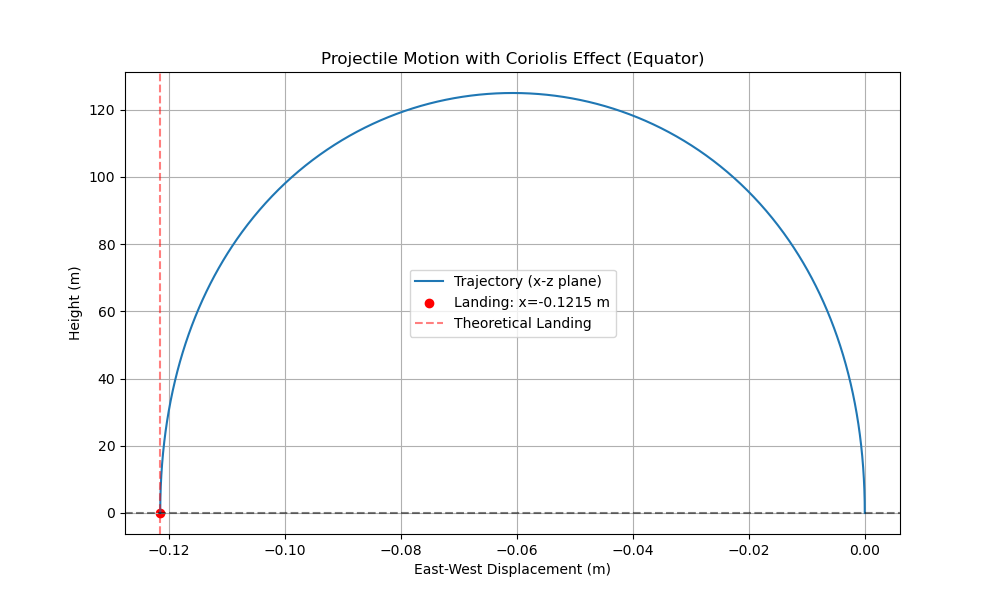
例子2：在赤道上抛出一个质点，显然上升过程中，科里奥利加速度的影响会使得物体的速度有个向西的分量，下降过程中的科里奥利加速度则会刚好抵消分量的增加，使得物体全过程向西偏移。可以很简单地推出理论公式：
$v_z(t)=v_0-gt,\quad a_x(t)=2\omega v_z(t),\quad v_x(t)=\int a_x(t)dt=2\omega(v_0t-\frac{1}{2}gt^2),\quad x(t)=\int v_x(t)dt=\omega(v_0t^2-\frac{1}{3}gt^3)$
代入$t=2v_0/g$，可以得到：
$x(t)=\omega\left(v_0\left(\frac{2v_0}{g}\right)^2-\frac{1}{3}g\left(\frac{2v_0}{g}\right)^3\right)=\frac{4\omega v_0^3}{g^2}-\frac{8\omega v_0^3}{3g^2}=\frac{4\omega v_0^3}{3g^2}$

科里奥利力

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# 常量
omega = 7.292e-5  # 地球自转角速度 (rad/s)
g = 10          # 重力加速度 (m/s²)
v0 = 50.0         # 初始上抛速度 (m/s)
h0 = 0.0          # 初始高度 (m)
lat = 0.0         # 赤道纬度 (rad)

# 运动方程：dy/dt = f(t, y), y = [x, y, z, vx, vy, vz]
def motion_eq(t, y):
    x, y, z, vx, vy, vz = y
    
    # 科里奥利加速度 (a_c = -2 ω × v)
    a_cx = -2 * omega * (-np.sin(lat) * vy + np.cos(lat) * vz)
    a_cy = -2 * omega * np.sin(lat) * vx
    a_cz = -2 * omega * np.cos(lat) * vx
    
    # 总加速度 (重力 + 科里奥利)
    ax = a_cx
    ay = a_cy
    az = -g + a_cz
    
    return [vx, vy, vz, ax, ay, az]

# 初始条件 [x, y, z, vx, vy, vz]
y0 = [0.0, 0.0, h0, 0.0, 0.0, v0]

# 模拟时间 (足够长以让质点落地)
t_span = (0, 10)  # 20秒足够上抛下落
t_eval = np.linspace(0, 10, 1000)

# 解微分方程
sol = solve_ivp(motion_eq, t_span, y0, t_eval=t_eval, rtol=1e-6)

# 提取轨迹
x, y, z = sol.y[0], sol.y[1], sol.y[2]

# 找到落地点 (z ≈ 0 的时刻)
landing_idx = 1000-1
landing_x, landing_y = x[landing_idx], y[landing_idx]
theory=-4/3*omega*v0**3/g**2

# 绘图
plt.figure(figsize=(10, 6))
plt.plot(x, z, label='Trajectory (x-z plane)')
plt.scatter(landing_x, 0, color='red', label=f'Landing: x={landing_x:.4f} m')
plt.axhline(0, color='black', linestyle='--', alpha=0.5)
plt.axvline(theory, color='red', linestyle='--', alpha=0.5,label='Theoretical Landing')
plt.xlabel('East-West Displacement (m)')
plt.ylabel('Height (m)')
plt.title('Projectile Motion with Coriolis Effect (Equator)')
plt.legend()
plt.grid()
plt.show()

# 输出结果
print(f"Initial position: (0, 0, {h0})")
print(f"Landing position: ({landing_x:.6f}, {landing_y:.6f}, 0)")
print(f"Westward displacement: {landing_x:.6f} m")