波动光学(衍射)
衍射导论
当光波遇到障碍物的时候,或多或少偏离几何光学的直线传播,这种现象统称为光的衍射。光的波长和孔径线度相当时,衍射现象尤为明显,且关系满足:
衍射现象可以使用惠更斯原理来解释,菲涅尔推导了衍射的数学表达式,称为惠更斯-菲涅尔原理:
菲涅尔衍射积分
从物理的角度考虑,可以给出$d\tilde{U}(P)$的决定因素:
- 面元大小$dS$;
- 次波源的振幅$\tilde{U_0}$;
- 次波源发射球面波到场点$\dfrac{e^{ikr}}{r}$;
- 倾角因子$f(\theta_0,\theta)=\frac12(\cos{\theta_0}+\cos{\theta})$。
引入比例常数$K$,可以得到:
此即为菲涅尔衍射积分表达式。
基尔霍夫衍射积分
基尔霍夫在$kr\gg 1$和$r\gg \lambda$的情况下,导出了无源空间边值定解的表达式:
表面上看,这只是明确了比例系数和倾斜因子;实际上,基尔霍夫衍射积分允许任意隔离光源和场点的闭合面,而不要求等相面。
基尔霍夫边界条件与傍轴衍射积分公式
取衍射屏面为$\Sigma_1$,无穷远半球面为$\Sigma_2$,衍射孔面为$\Sigma_0$,则有:
将基尔霍夫衍射积分公式代入,得到:
可以做基尔霍夫边界条件的假设,$\Sigma_1$和$\Sigma_2$的积分可以忽略,得到:
在傍轴条件下,还可以进一步简化:
衍射的分类
衍射现象可以分为两类:
- 菲涅尔衍射:近场衍射,光源和屏幕距离较近;
- 夫琅禾费衍射:远场衍射,光源和屏幕距离无限远(或者衍射孔线度无线小)。
巴比涅原理
如果$\Sigma_a$和$\Sigma_b$是两个不同的互补衍射屏面,且它们的衍射场分别为$\tilde{U_a}$和$\tilde{U_b}$,则有:
对于夫琅禾费衍射尤其方便,因为光线聚集在后焦点,轴外的自由光场为零,那么:
这说明两者的衍射图样除了像点完全相同。
菲涅尔圆孔衍射
半波带法
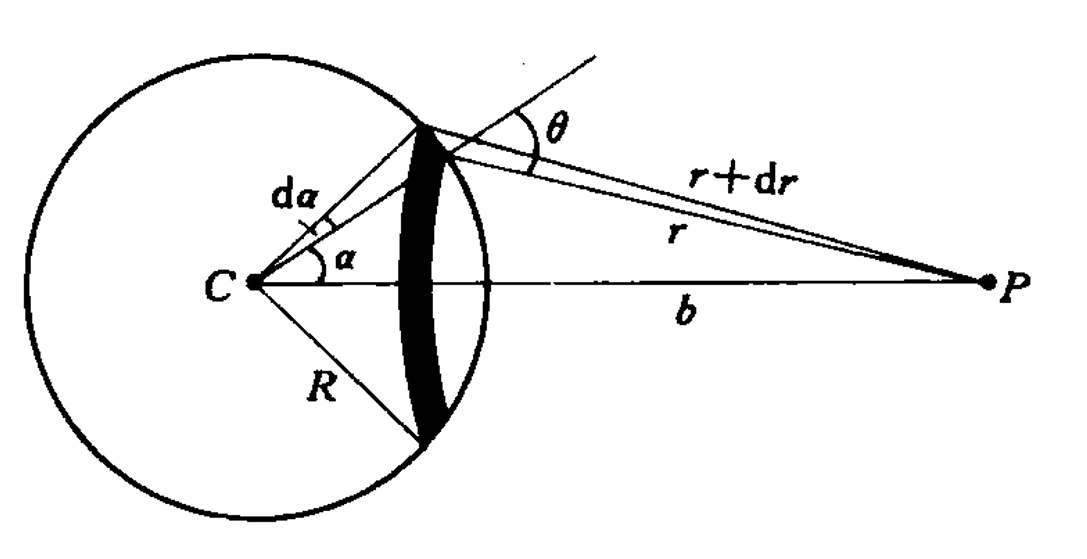
处理圆孔衍射很自然的一个想法是将衍射孔的波前分割为一个个波带,每个波带的相位差为$\lambda/2$,这样,只需要确定最后一个波带的相位,就能定性确定接受屏的强度分布。
不过,我们需要考证每个波带的振幅是否相同。写出每个波带的振幅:
通过简单的数学运算,可以得到:
这说明每个半波带的振幅和$r$是无关的,只和$f(\theta_k(r_k))$有关。我们可以写出这一泛函的表达式:
代入$\lambda\sim 100nm,b\sim 1m,R\sim 1m$可知,振幅随着波带数的变化及其缓慢。
做题的时候,只需要知道以下公式:
- 最大波带半径:$r_{max}=\sqrt{b^2+R^2\sin^2\alpha}=b+k\frac{\lambda}{2}$
- 最大波带数:$k_{max}=2\dfrac{r_{max}-b}{\lambda}$
- 第k级波带半径:$\rho_k=\sqrt{k}\rho_1,\rho_1=\sqrt{\dfrac{Rb\lambda}{R+b}}$
- 最大波带数:$k_{max}=(\dfrac1R+\dfrac1b)\dfrac{\rho_{max}^2}{\lambda}$
以$\rho$为变量,最大半径和最小半径之间的差值为:
所以:
利用以上特性,可以绘制菲涅尔波带片,在奇数或偶数的波带 上涂黑,即可增强光强。菲涅尔波带片就像透镜,可以将入射光汇聚起来,可以将上式改写为:
等效焦距为$f=\frac{\rho_k^2}{k\lambda}=\frac{\rho_1^2}{\lambda}$。
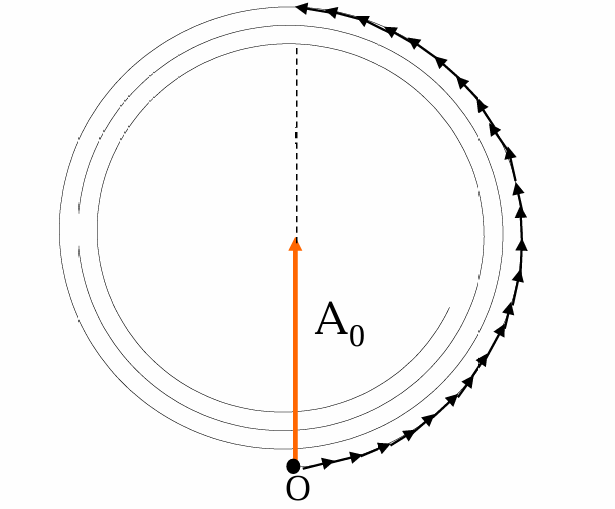
如果k并非整数,可以通过矢量图解来解决问题:以自由光强的振幅为$A_0$,其代表了参考圆的半径。给定波带数$k$,可以从参考圆上的某点出发,绕$k/2$圈得到最终的振幅。自由光强的振幅等效于绕$\infty$圈(半径不断缩小)得到的振幅。
单缝夫琅禾费衍射
利用傍轴的基尔霍夫衍射公式:
假定缝宽为$b$,长度为$a$,坐标原点沿$\theta$方向到场点P的距离为$L_0$。那么可以计算出:
光强分布为:
当$\theta$较小的时候,利用近似得到零级衍射光斑的半角宽度:
关于后焦面接受的球面波的振幅说明:记到达透镜的振幅为$A_m$,出透镜的振幅为$A_N=A_M$,到达后焦面的振幅为$A_p$。根据反比关系:
得到:
对于斜入射的情况,宗量变为:
相应地,衍射积分的结果变为:
光强分布变为:
相应地,半角宽度变为:
矩孔夫琅禾费衍射
所以光强变为:
圆孔夫琅禾费衍射
圆孔夫琅禾费衍射是最有实际应用的模型之一,因为大多数望远镜都满足圆孔夫琅禾费衍射的条件。
用到了贝塞尔函数的积分定义式:
和贝塞尔函数的递推公式:
所以最后的光强为:
考虑系数,$I_0=\frac{\pi^2a^4}{\lambda^2f^2}A^2$。
第一个零点的位置为:
或表示为直径的更熟悉的形式:
夫琅禾费多缝衍射
与多缝干涉类似,多缝衍射也可以使用累加方法处理:
所以光强分布为:
当$\sin\beta=0$时,产生主极大:
对比原来的极大值:
可见新产生的极大值与原来的极大值和缝数无关。但是$\sin N\beta=0$的时候,原来的极大值会被破坏:
正弦光栅
正弦光栅的透过率函数为:
透过率函数只会影响单缝衍射因子,而不会影响缝间干涉因子。所以可以得到单缝衍射因子为:
所以光强分布为:
光栅光谱仪
被称为光栅方程,$d$为光栅常数,$n$为衍射级次。两边取微分,得到:
角色散本领定义为:
线色散本领定义为:
色分辨本领定义为:
闪耀光栅
透射光栅由于光能主要集中在0级主极大上,导致其他光谱级的强度较小,这是由于单元衍射因子和单元干涉因子之间存在0级主极大的重叠。解决的办法也很简单,即通过闪耀光栅调制单元干涉因子。闪耀光栅的光程差为:
$\theta_b$为槽面和光栅平面的夹角。当$\theta_b$为0时,退化到普通光栅。当$\theta_b$满足:
时,干涉因子将以第n级极大为中心,从而将光强集中在第n级极大上。