表面光学
电磁场边值关系
介质分界面两侧的电磁场有突变,遵循麦克斯韦方程组:
四个方程取积分极限,可得无电荷电流介质表面的边值关系:
写为电场和磁感应强度的分量形式:
菲涅尔公式
利用电磁场的边值关系,考虑平面单色光入射到介质分界面,分为s(senkrecht)振动分量和p(parallel)振动分量。s分量的电场矢量垂直于入射面,p分量的电场矢量平行于入射面。记入射电场复振幅为$\widetilde{E}_{1s/p}$,折射复振幅为$\widetilde{E}_{2s/p}$,反射分复振幅为$\widetilde{E}_{1s/p}’$。根据边值关系,得到菲涅尔公式:
证明:先计算s分量:
利用$H=\sqrt{\frac{\epsilon}{\mu}}E$,得到:
利用$n^2=\sqrt{\epsilon\mu}$得到:
由$n_1\sin{i_1}=n_2\sin{i_2}$,得知第一条方程等价于第二条方程,剩下两条方程解得:
p分量同理:
变为:
发现第二条方程和第三条方程等价,由上两条方程及近似$\mu_1=\mu_2$可得:
值得注意的是,菲涅尔公式有下述成立条件:
- 适用于绝缘介质,否则金属表面容易存在电荷和电流;
- 适用于各向同性介质;
- 适用于线性介质;
- 适用于光频段,此时磁化机制冻结,$\mu\approx1$。当然,也可以在上述推导的基础上推出计算磁导率的菲涅尔公式。
反射率和折射率(振幅关系)
由菲涅尔公式可得复振幅反射率和复振幅折射率:
相应地,光强反射率和折射率为:
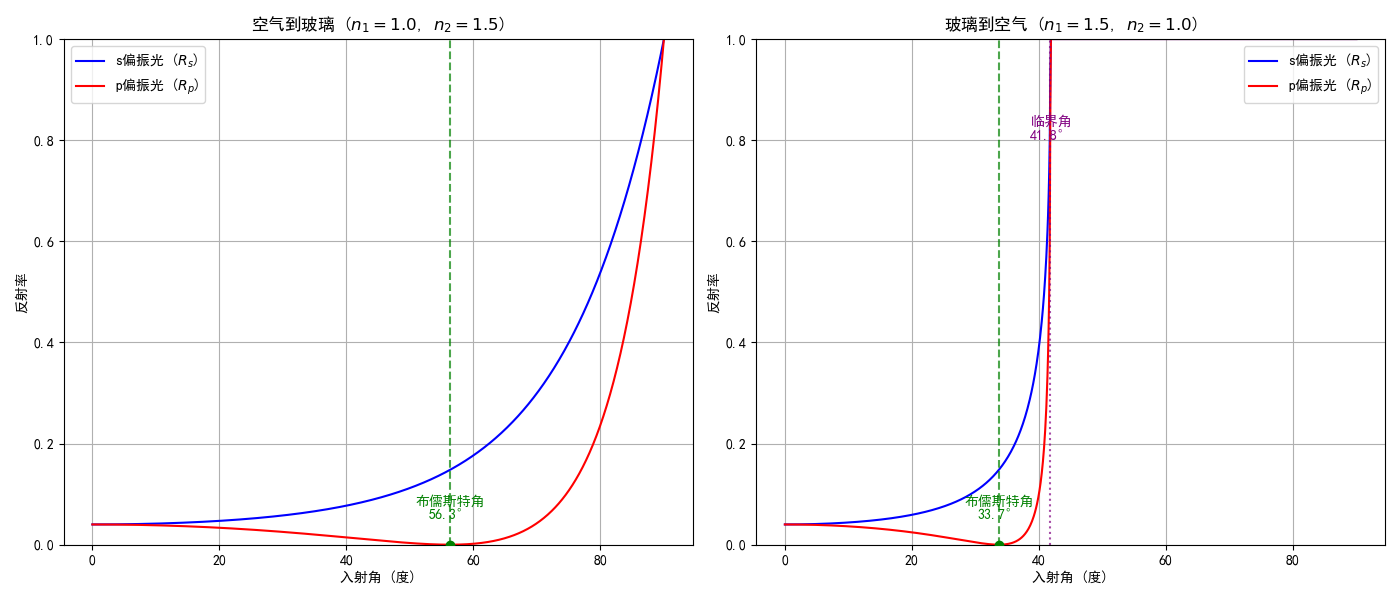
对于给定的折射率,反射率的变化图像如下:
绘图代码:import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 设置中文字体(确保系统已安装 SimHei 字体)
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False # 解决负号显示问题
def calculate_reflectivity(n1, n2):
"""计算反射率 Rs 和 Rp"""
angles = np.linspace(0, 90, 1000)
angles_rad = np.deg2rad(angles)
Rs = np.zeros_like(angles)
Rp = np.zeros_like(angles)
for i, angle in enumerate(angles_rad):
sin_i2 = (n1 / n2) * np.sin(angle)
if sin_i2 > 1:
# 全反射
Rs[i] = 1
Rp[i] = 1
else:
i2 = np.arcsin(sin_i2)
# Rs 公式
numerator_s = n1 * np.cos(angle) - n2 * np.cos(i2)
denominator_s = n1 * np.cos(angle) + n2 * np.cos(i2)
Rs[i] = (abs(numerator_s / denominator_s)) ** 2
# Rp 公式
numerator_p = n2 * np.cos(angle) - n1 * np.cos(i2)
denominator_p = n2 * np.cos(angle) + n1 * np.cos(i2)
Rp[i] = (abs(numerator_p / denominator_p)) ** 2
return angles, Rs, Rp
def plot_reflectivity(ax, n1, n2, title):
"""绘制反射率曲线"""
angles, Rs, Rp = calculate_reflectivity(n1, n2)
# 计算布儒斯特角
i_B = np.arctan(n2 / n1) * 180 / np.pi
# 计算临界角(仅当 n1 > n2 时存在)
critical_angle = np.arcsin(n2 / n1) * 180 / np.pi if n1 > n2 else None
# 绘制曲线
ax.plot(angles, Rs, label='s偏振光 ($R_s$)', color='blue')
ax.plot(angles, Rp, label='p偏振光 ($R_p$)', color='red')
# 标注布儒斯特角
ax.axvline(i_B, color='green', linestyle='--', alpha=0.7)
ax.scatter(i_B, 0, color='green', zorder=5)
ax.text(i_B, 0.05, f'布儒斯特角\n{i_B:.1f}°', ha='center', color='green')
# 标注临界角(如果存在)
if critical_angle and critical_angle < 90:
ax.axvline(critical_angle, color='purple', linestyle=':', alpha=0.7)
ax.text(critical_angle, 0.8, f'临界角\n{critical_angle:.1f}°', ha='center', color='purple')
# 设置标题和标签
ax.set_title(title)
ax.set_xlabel('入射角 (度)')
ax.set_ylabel('反射率')
ax.legend()
ax.grid(True)
ax.set_ylim(0, 1)
# 创建画布和子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 情况1:n1=1.0(空气)→ n2=1.5(玻璃)
plot_reflectivity(ax1, n1=1.0, n2=1.5, title='空气到玻璃 ($n_1=1.0$, $n_2=1.5$)')
# 情况2:n1=1.5(玻璃)→ n2=1.0(空气)
plot_reflectivity(ax2, n1=1.5, n2=1.0, title='玻璃到空气 ($n_1=1.5$, $n_2=1.0$)')
plt.tight_layout()
plt.show()
s偏振方向的反射率单调上升,而p偏振方向先下降到0再上升。其中存在两个特殊的角度:
- 布儒斯特角:当:此时,反射光和折射光垂直。可以导出布儒斯特角公式:
- 全反射角:当$n_1>n_2$时,$i_2=\frac{\pi}{2}$,即全反射角:
相位关系
除了考虑振幅关系,由(1-4)式可知,当入射角度大于全反射角时,由于:
会出现复数情况。这时候,反射光和折射光的相位分析会比较复杂。考虑复数情况,我们写出:
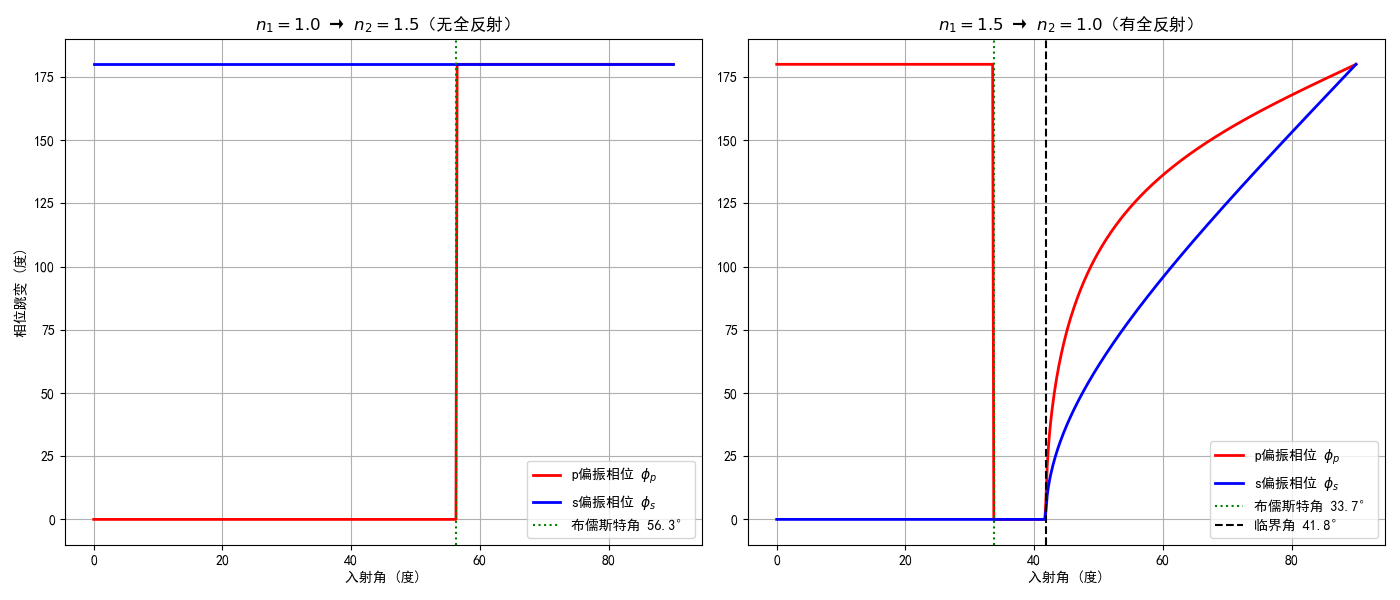
对于反射情形,当$n_1<n_2$,可以得到:
当$n_1>n_2$,可以得到:
值得注意的是,本来应该存在的负号因为相位符号的约定(超前取负号,落后取正号)而被抵消了。
图片如下:
绘图代码:import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 设置中文字体和负号显示
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
def calculate_phase(n1, n2):
"""计算反射系数的相位跳变,严格按分段公式处理"""
i_c = np.arcsin(n2 / n1) if n1 > n2 else None # 临界角(仅当n1 > n2)
i_B = np.arctan(n2 / n1) # 布儒斯特角
angles = np.linspace(0.01, 90, 500)
angles_rad = np.deg2rad(angles)
phi_p, phi_s = np.zeros_like(angles), np.zeros_like(angles)
for i, angle in enumerate(angles_rad):
sin_i1 = np.sin(angle)
sin_i2 = (n1 / n2) * sin_i1
if sin_i2 > 1: # 全反射条件(仅当n1 > n2)
cos_i1 = np.cos(angle)
term = np.sqrt(sin_i1**2 - (n2/n1)**2)
# p偏振相位(全反射区域)
phi_p[i] = 2 * np.arctan((n1**2 * term) / (n2**2 * cos_i1))
# s偏振相位(全反射区域)
phi_s[i] = 2 * np.arctan(term / cos_i1)
else:
cos_i1 = np.cos(angle)
cos_i2 = np.sqrt(1 - sin_i2**2)
# 判断p偏振相位
tan_num = np.tan(angle - np.arcsin(sin_i2))
tan_den = np.tan(angle + np.arcsin(sin_i2))
if n1 < n2:
phi_p[i] = 0 if tan_num / tan_den > 0 else np.pi # 公式1
else:
if angle < i_B:
phi_p[i] = np.pi if tan_num / tan_den < 0 else 0 # 公式2
else:
phi_p[i] = 0 if tan_num / tan_den > 0 else np.pi # 公式2
# 判断s偏振相位
sin_num = np.sin(np.arcsin(sin_i2) - angle)
sin_den = np.sin(np.arcsin(sin_i2) + angle)
if n1 < n2:
phi_s[i] = np.pi if sin_num / sin_den < 0 else 0 # 公式1
else:
if angle < i_c:
phi_s[i] = 0 if sin_num / sin_den > 0 else np.pi # 公式2
else:
phi_s[i] = 2 * np.arctan(np.sqrt(sin_i1**2 - (n2/n1)**2) / cos_i1) # 公式2
return angles, np.rad2deg(phi_p), np.rad2deg(phi_s), np.rad2deg(i_B), np.rad2deg(i_c) if i_c else None
# 创建画布和子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 情况1:n1=1.0 < n2=1.5(空气到玻璃)
angles, phi_p, phi_s, i_B, _ = calculate_phase(n1=1.0, n2=1.5)
ax1.plot(angles, phi_p, label='p偏振相位 $\phi_p$', color='red', linewidth=2)
ax1.plot(angles, phi_s, label='s偏振相位 $\phi_s$', color='blue', linewidth=2)
ax1.axvline(i_B, color='green', linestyle=':', label=f'布儒斯特角 {i_B:.1f}°')
ax1.set_title('$n_1=1.0$ → $n_2=1.5$(无全反射)')
ax1.set_xlabel('入射角 (度)')
ax1.set_ylabel('相位跳变 (度)')
ax1.legend()
ax1.grid(True)
ax1.set_ylim(-10, 190) # 留出标注空间
# 情况2:n1=1.5 > n2=1.0(玻璃到空气)
angles, phi_p, phi_s, i_B, i_c = calculate_phase(n1=1.5, n2=1.0)
ax2.plot(angles, phi_p, label='p偏振相位 $\phi_p$', color='red', linewidth=2)
ax2.plot(angles, phi_s, label='s偏振相位 $\phi_s$', color='blue', linewidth=2)
ax2.axvline(i_B, color='green', linestyle=':', label=f'布儒斯特角 {i_B:.1f}°')
ax2.axvline(i_c, color='black', linestyle='--', label=f'临界角 {i_c:.1f}°')
ax2.set_title('$n_1=1.5$ → $n_2=1.0$(有全反射)')
ax2.set_xlabel('入射角 (度)')
ax2.legend()
ax2.grid(True)
ax2.set_ylim(-10, 190)
plt.tight_layout()
plt.show()
有时候,我们只关心极限条件下是否存在半波损失。注意上述相位是在参考坐标系下的计算,对于p光,相位为0恰恰意味着有半波损。整理表格如下:
对于s偏振光:
| 折射率关系 | 正入射 | 掠入射 |
|---|---|---|
| $n_1<n_2$ | 有 | 有 |
| $n_1>n_2$ | 无 | 有 |
对于p偏振光:
| 折射率关系 | 正入射 | 掠入射 |
|---|---|---|
| $n_1<n_2$ | 有 | 有 |
| $n_1>n_2$ | 无 | 有 |
对于折射情形,当$n_1<n_2$,反射率恒正,不存在半波损的问题。
当$n_1>n_2$,在全反射角后出现复数情况,可以得到:
神奇的是,讨论折射的相位变化并不是平凡的事情,因为按照虚波矢理论:
可以得到:
这意味着折射光强是指数衰减的,这个全反射角的定义相符。不过,在研究近场光学时,古斯汉森位移指出其大小正比于:
可以发现p偏振由于相位变化更快,导致古斯汉森位移更大。





