矩阵光学
Introduction and Assumptions
矩阵光学指的是通过线性变换矩阵来描述几何光学传播过程的方法。这其中隐含了几个假设:
- 光线是直线(这也是几何光学的基本假设);
- 光线的传播是线性的;
- 光线满足傍轴近似(即光线的角度很小)。
我们用两个参数来描述光线的传播——光线的位置和方向:
光线通过线性变换矩阵$M$传播后,位置和方向变为:
显然,矩阵$M$是一个$2 \times 2$的矩阵:
如果我们有多个光学元件,每个元件都有一个传播矩阵$M_i$,那么这些元件的传播矩阵的乘积就是整个系统的传播矩阵:
Sign Convention
在矩阵光学中,我们使用以下符号约定:
- 物距和像距的正负遵循“实正虚负”的规则;
- 光线角度的正负遵循“逆时针正顺时针负”的规则;
- 所有的曲面界面,曲率中心在右侧为正,左侧为负;
- 以上约定均在光线的传播方向上定义。
Some Examples
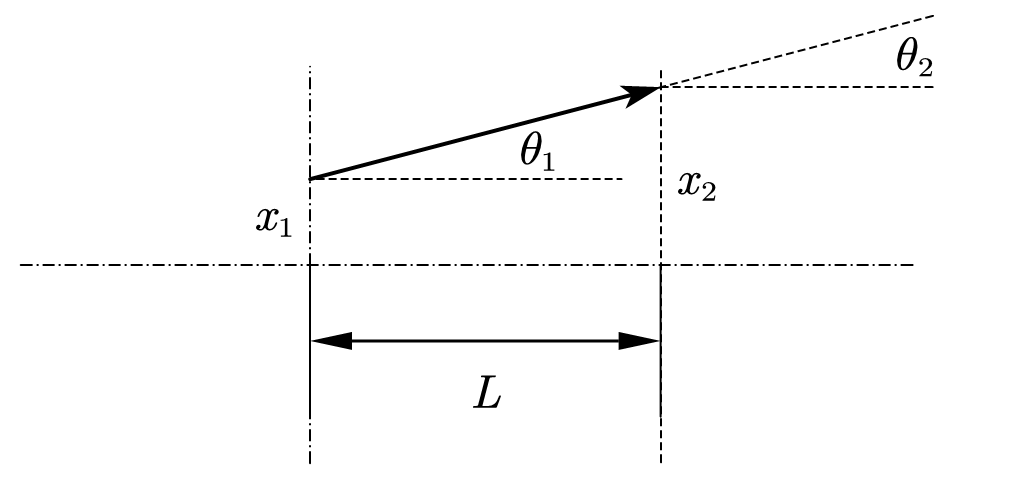
Free Space
自由空间中的光线传播是最简单的情况,传播矩阵是:
可以通过简单的推导验证:
Surface and Parallel Plate
光线入射介质$n_1$,出射介质$n_2$满足以下光学矩阵:
可以通过简单的推导验证:由折射定理,我们有:
平行板是一个简单的光学元件,传播矩阵可以通过三个光学矩阵相乘得到:
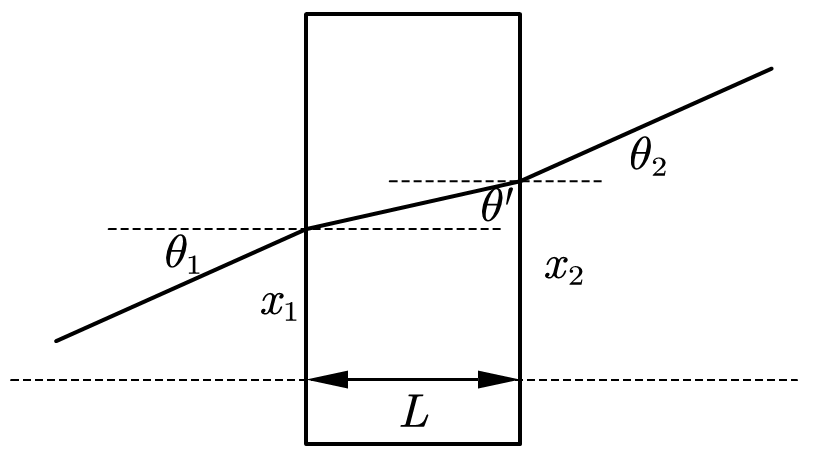
这说明相比于自由空间的传播,平行板的传播矩阵不会改变光线的角度,只会按折射率改变光线的位置。相应的,可以推出多个平行板的传播矩阵:
Reflective spherical mirrors
反射球面镜的光学矩阵:
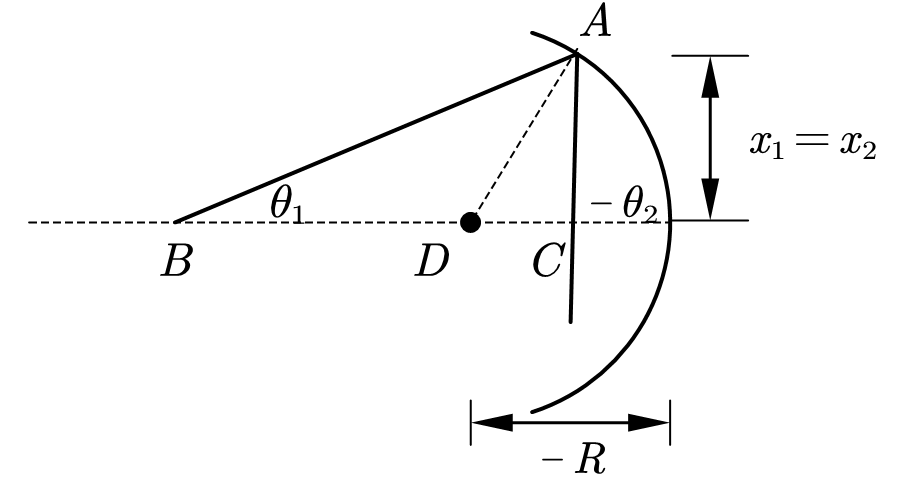
尤其注意这里的符号约定,如图所示曲率中心在左侧,则对于该凹面镜反射,矩阵应该是:
对于谐振腔的稳定性计算:
由$T^n,(T=\begin{pmatrix} A & B\\ C & D \end{pmatrix})$的稳定性条件$\frac12|A+D|<1$得到:
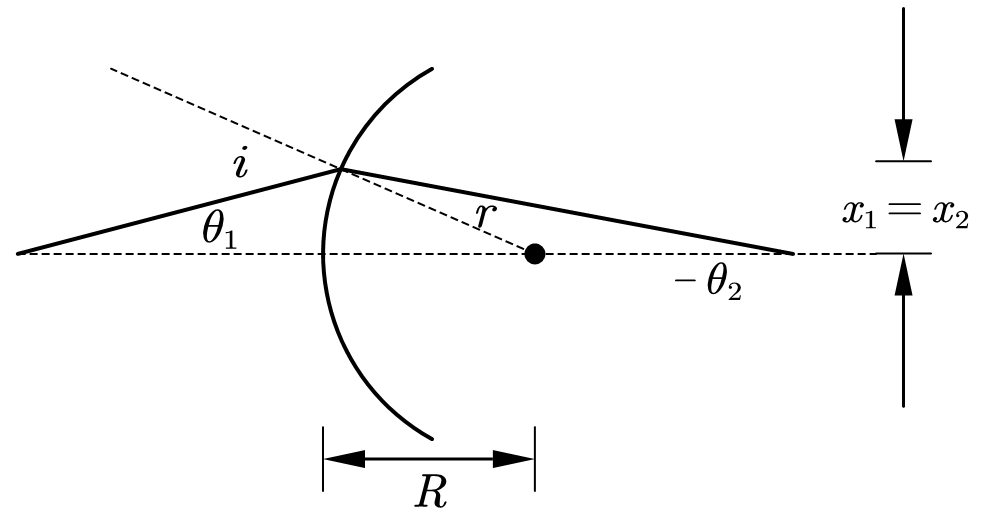
Refractive spherical surfaces
折射球面的光学矩阵:
当$R\rightarrow \infty$时,球面变为平面,折射球面的光学矩阵变为折射平面的光学矩阵:
Thin lens
薄透镜的光学矩阵可以通过两个折射球面的光学矩阵相乘得到:
其中$f$是透镜的焦距:
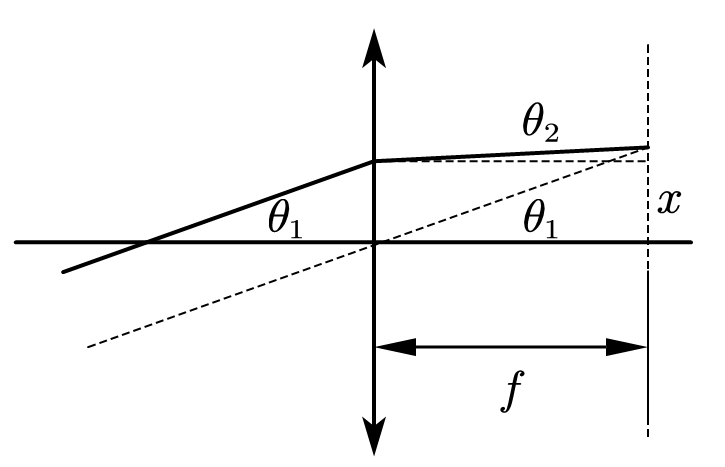
薄透镜将平行光束汇聚到焦点:
Physical Meaning of the Matrix Elements
通过运算线性变换矩阵的元素,我们可以得到一些物理意义:
- 当满足成像条件的时候,光线汇聚的位置和角度无关,即$B=0$
- 这表明$A=\frac{x’}{x}$表示成像放大率;
- $\theta’=Cx+D\theta$表明$\delta\theta’=D\delta\theta$,即$D$表示光线的角度放大率;
- 满足成像条件时,$B=0$,表面其物理意义是成像传输距离。
- 当满足聚焦条件的时候,平行光线聚焦在一点上,即$A=D=0$(成像放大率为0,即聚焦):
- $C=\frac{\theta’}{x}=-\frac{1}{f}$表示负屈光度。
所以传输矩阵的物理意义是:
Relations between the Matrix Elements
传输矩阵的元素之间有一些关系:
其物理意义是光束的能流守恒。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 小径!





