Introduction

多电子系统

许多电子系统的结构和动力学性质是理论物理和化学中的基本问题。这些系统包括：

• 原子
• 分子
• 介观系统（如团簇、量子点）
• 固体（包括层状结构、表面和准晶体）

这些系统的性质可以分为结构性质（如电子壳层结构、结合能、电/磁矩、几何构型）和动力学性质（如电子激发谱、光谱性质、散射过程等）。

研究这些性质的两种主要方法是：基于薛定谔方程的第一性原理计算（ab-initio）方法和基于模型哈密顿量（model Hamiltonian）的方法。密度泛函理论（DFT）就是基于前者的理论。

可以写出多体系统的哈密顿量为：

$$\hat{H} = \hat{T}_n + \hat{V}_{n-n} + \hat{H}_{e}$$ $$\hat{H}_{e} = \hat{T}_e+\hat{V}_{n-e}+\hat{V}_{e-e}$$

其中，$\hat{T}_n$是原子核动能：

$$\hat{T}_n = -\sum_{I}\frac{\hbar^2}{2M_I}\nabla_I^2$$

$\hat{V}_{n-n}$是原子核间相互作用：

$$\hat{V}_{n-n} = \sum_{I<J}\frac{Z_IZ_Je^2}{|\mathbf{R}_I-\mathbf{R}_J|}$$

$\hat{T}_e$是电子动能：

$$\hat{T}_e = -\sum_{i}\frac{\hbar^2}{2m_e}\nabla_i^2$$

$\hat{V}_{n-e}$是原子核和电子间相互作用：

$$\hat{V}_{n-e} = -\sum_{i,I}\frac{Z_Ie^2}{|\mathbf{r}_i-\mathbf{R}_I|}$$

$\hat{V}_{e-e}$是电子间相互作用：

$$\hat{V}_{e-e} = \sum_{i<j}\frac{e^2}{|\mathbf{r}_i-\mathbf{r}_j|}$$

这样的哈密顿量当然还存在近似：

• 忽视了动能项的相对论效应；
• 忽视了原子核的大小；
• 忽视了带电粒子间的作用的相对论效应；

科学家们为了解决这些问题，提出了一系列近似方法：

• 从波函数的角度出发，提出了Hartree近似、Hartree-Fock近似；
• 从哈密顿量近似的角度出发，提出了Thomas-Fermi模型、Thomas-Fermi-Dirac模型，他们都是基础的密度泛函理论。

Born-Oppenheimer近似

即便是这样近似的哈密顿量，仍然是超级复杂的：

$$\hat{H}\Psi(\mathbf{R}_1,\cdots,\mathbf{R}_N,\mathbf{r}_1\sigma_1,\cdots,\mathbf{r}_n\sigma_n) = E\Psi(\mathbf{R}_1,\cdots,\mathbf{R}_N,\mathbf{r}_1\sigma_1,\cdots,\mathbf{r}_n\sigma_n)$$

可以认为由于原子核极重，原子核波函数和电子波函数可以分离，这就是Born-Oppenheimer近似（又称为绝热近似）。这样，我们可以将多体系统的波函数分解为电子波函数和原子核波函数的乘积：

$$\Psi(\mathbf{R}_1,\cdots,\mathbf{R}_N,\mathbf{r}_1\sigma_1,\cdots,\mathbf{r}_n\sigma_n) = \Psi_n(\mathbf{R}_1,\cdots,\mathbf{R}_N)\Psi_e(\mathbf{r}_1\sigma_1,\cdots,\mathbf{r}_n\sigma_n)$$

Hartree近似

最简单的对电子波函数的近似是Hartree近似，即认为电子波函数是独立的，这样的波函数可以写为：

$$\Phi_e(\mathbf{r}_1\sigma_1,\cdots,\mathbf{r}_n\sigma_n) = \prod_{i=1}^{n}\psi_i(\mathbf{r}_i\sigma_i)$$

考虑电子波函数的能量：

$$\begin{aligned} E[\Phi] = \langle\Phi|\hat{H}_e|\Phi\rangle &= \sum_{i=1}^{n}\sum_{\sigma=\uparrow,\downarrow}\langle\psi_i|-\frac{\hbar^2\nabla^2}{2m}+V_{ext}|\psi_i\rangle \\&+ \frac{1}{2}\sum_{i,j=1}^{n}\sum_{\sigma,\sigma'=\uparrow,\downarrow}\int\int d\mathbf{r}_id\mathbf{r}_j\frac{e^2}{|\mathbf{r}_i-\mathbf{r}_j|}|\psi_i|^2|\psi_j|^2 \end{aligned}$$

通过变分原理，得到：

$$\left[-\frac{\hbar^2\nabla^2}{2m}+V_{ext}(\mathbf{r})+V_H(\mathbf{r})\right]\psi_i(\mathbf{r}) = \varepsilon_i\psi_i(\mathbf{r})$$

其中，$V_H(\mathbf{r})$是Hartree势，表示其他电子对第i个电子产生的平均场：

$$V_H(\mathbf{r}) = \int d\mathbf{r}'\frac{e^2}{|\mathbf{r}-\mathbf{r}'|}\rho(\mathbf{r}')$$

Hartree-Fock近似与Self-Consistent Field方法

Hartree近似虽然考虑了电子间的相互作用，但是没有考虑交换效应，其波函数也不是反对称的。Hartree-Fock方法就是在Hartree近似的基础上，考虑电子波函数的反对称性：

$$\Phi_e(\mathbf{r}_1\sigma_1,\cdots,\mathbf{r}_n\sigma_n) = \frac{1}{\sqrt{n!}}\begin{vmatrix}\psi_1(\mathbf{r}_1\sigma_1)&\cdots&\psi_n(\mathbf{r}_1\sigma_1)\\\vdots&\ddots&\vdots\\\psi_1(\mathbf{r}_n\sigma_n)&\cdots&\psi_n(\mathbf{r}_n\sigma_n)\end{vmatrix}$$

此后用$\Phi$来表示独立电子波函数，而用$\Psi$来表示多体波函数。

我们接下来就要推导出HF方程。先考虑电子波函数能量：

$$\begin{aligned} E[\Phi] = \langle\Phi|\hat{H}_e|\Phi\rangle&= \sum_{i=1}^{n}\sum_{\sigma=\uparrow,\downarrow}\langle\psi_i|-\frac{\hbar^2\nabla^2}{2m}+V_{ext}|\psi_i\rangle \\&+ \frac{1}{2}\sum_{i,j=1}^{n}\sum_{\sigma,\sigma'=\uparrow,\downarrow}\left[\langle\psi_i\psi_j|\frac{e^2}{|\mathbf{r}_i-\mathbf{r}_j|}|\psi_i\psi_j\rangle - \langle\psi_i\psi_j|\frac{e^2}{|\mathbf{r}_i-\mathbf{r}_j|}|\psi_j\psi_i\rangle\right] \end{aligned}$$

对其做变分，得到HF方程：

$$\begin{aligned} \left[-\frac{\hbar^2\nabla^2}{2m}+V_{ext}(\mathbf{r})+V_H(\mathbf{r})+V^{HF}_{x}(\mathbf{r},\mathbf{r'})\right]\psi_i(\mathbf{r}) &= \varepsilon_i\psi_i(\mathbf{r}) \end{aligned}$$

其中，$V^{HF}_{x}(\mathbf{r},\mathbf{r’})$是交换势：

$$V^{HF}_{x}(\mathbf{r},\mathbf{r'}) = - \frac{e^2}{|\mathbf{r}-\mathbf{r}_j|}\sum_{j=1}^{n}\sum_{\sigma,\sigma'=\uparrow,\downarrow}\psi_j^*(\mathbf{r})\psi_j(\mathbf{r'})$$

除了平均场的库伦能、电子交换反对称的交换能，还有因为行列式近似导致的关联能。

数值计算中，常用基组波函数来展开电子波函数：

$$\psi_i(\mathbf{r}) = \sum_{\mu}C_{\mu i}\phi_{\mu}(\mathbf{r})$$

通常可以选择：

• 平面波基组：适用于周期性体系；
• 高斯基组：适用于分子和小团簇；
• 原子轨道基组：适用于分子和固体表面。

这样，我们就有了成体系的HF方法：

• 猜测初始的密度矩阵，并计算哈密顿量和重叠矩阵；
• 计算Fock矩阵，对角化得到新的波函数和能量；
• 用新的波函数计算新的密度矩阵，直到收敛。

Hohenberg-Kohn定理

Hohenberg-Kohn定理是DFT理论的基础。它的内容是：

• 给定一个基态的电子密度分布$n_0(\mathbf{r})$，体系的哈密顿量$\hat{H}$和外势$V_{ext}(\mathbf{r})$是唯一确定的。
  • 两个不同的哈密顿量$\hat{H}$不会具有相同的基态；
  • 两个不同的哈密顿量$\hat{H}$对应的基态空间，不会具有相同的基态电子密度分布$n_0(\mathbf{r})$；
• 给定一个外势$V_{ext}(\mathbf{r})$，可以定义能量泛函$E[n]$，使得体系的基态能量$E_0$是这个泛函的最小值。

用公式表示就是：

$$V_{ext}(\mathbf{r})\Leftrightarrow |\Psi_0\rangle\Leftrightarrow n_0(\mathbf{r})$$

第一定理

我们先证明第一个定理的第一部分：同一个基态是否可以对应两个不同的哈密顿量？

$$\hat H_1|\Psi_0\rangle = E_0|\Psi_0\rangle, \quad \hat H_2|\Psi_0\rangle = E_0|\Psi_0\rangle$$

哈密顿量仅有外势项不同：

$$[(V_{ext1}(\mathbf{r})-V_{ext2}(\mathbf{r}))-(E_1-E_2)]|\Psi_0\rangle = 0$$

仅有可能有两种情况：

• $V_{ext1}(\mathbf{r})-V_{ext2}(\mathbf{r}) =E_1-E_2$；
• $|\Psi_0\rangle$是零态；

这样便完成了第一定理的第一部分的证明。接着是第二部分的证明：同一个基态是否可以对应两个不同的基态电子密度分布$n_0(\mathbf{r})$？

假定两个哈密顿量$\hat H_1,\hat H_2$对应的基态电子密度分布相同，即$n_0(\mathbf{r})$。那么，两个哈密顿量的基态波函数$\Psi_0^{(1)},\Psi_0^{(2)}$由变分原理有：

$$\langle \Psi_0^{(1)}|\hat H_2|\Psi_0^{(1)}\rangle >E_2, \quad \langle \Psi_0^{(2)}|\hat H_1|\Psi_0^{(2)}\rangle >E_1$$

这样就有：

$$\langle \Psi_0^{(1)}|\hat H_1+V_{ext2}-V_{ext1}|\Psi_0^{(1)}\rangle >E_2, \quad \langle \Psi_0^{(2)}|\hat H_2+V_{ext1}-V_{ext2}|\Psi_0^{(2)}\rangle >E_1$$

二者相加有：

$$E_1+E_2>E_2+E_1$$

第二部分得证。

第二定理

由第一部分，基态的电子密度与哈密顿量是一一对应的。那么，我们可以定义能量泛函$E[n]$，使得体系的基态能量$E_0$是这个泛函的最小值，同时电子密度$n_0(\mathbf{r})$是基态波函数对应的电子密度。

对于可能存在基态简并的体系，即便同一个哈密顿量可能对应不同的基态波函数和电子密度，但给定基态电子密度仍然唯一对应了基态能量，也就是说，能量仍可以表示为电子密度的泛函。

HK定理其实是non-trivial的，因为按照传统的观念，能量应该是波函数的泛函：

$$E[\Psi] = \langle\Psi|\hat{H}|\Psi\rangle$$

现在我们知道，能量是电子密度的泛函，自由度一下子从$3N$个变为了3个。但HK定理关于能量泛函的存在性并没有给出具体的形式。一般而言，可以将总能量分解为：

$$E[n] = T[n]+V_{ext}[n]+E_H[n]$$

其中，外势场还比较容易给出：

$$V_{ext}[n] = \int d\mathbf{r}n(\mathbf{r})V_{ext}(\mathbf{r})$$

但是电子动能和电子相互作用可难以表示为电子密度的泛函。为此，科学家们做了很多近似，比如对电子做了经典库伦能近似：

$$J[n]=\frac{1}{2}\int\int d\mathbf{r}d\mathbf{r}'\frac{n(\mathbf{r})n(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}$$

但是$J[n]$没有包括电子作为费米子的交换和关联作用。

Thomas-Fermi-Dirac近似

将电子视为均匀分布的气体，电子系统的能量可以表示为电子密度的泛函，这样的方法称为Thomas-Fermi近似。这几项都可以表示为电子密度的泛函：

$$\begin{aligned} T[n] &= C_1\int d\mathbf{r}n^{\frac53}(\mathbf{r}),C_1=\frac{3}{10}(3\pi^2)^\frac23 \\ V_{ext}[n] &= \int d\mathbf{r}n(\mathbf{r})V_{ext}(\mathbf{r}) \\ E_H[n] &= \frac{1}{2}\int\int d\mathbf{r}d\mathbf{r}'\frac{n(\mathbf{r})n(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} \end{aligned}$$

Thomas-Fermi近似没有考虑交换能的影响，Dirac发展了Thomas-Fermi-Dirac近似，考虑了交换能：

$$E_{xc}[n] = C_2\int d\mathbf{r}n^{\frac43}(\mathbf{r}),C_2=-\frac{3}{4}\left(\frac{3}{\pi}\right)^\frac13$$

（这样做的误差反而更大了，原来是因为TF模型本身存在误差抵消）。此外，还有Thomas-Fermi-Dirac—Weizsacker近似。TFD模型由于对动能的近似过于简单，而动能恰好和总能量是一个量级的，所以计算误差较大。TFD模型是Orbitals-Free DFT的基础，由于复杂度是$O(N\log N)$，所以适用于大规模的计算。

Microsoft和Abacus尝试用AI学习泛函来发展OFDFT，具体可见如何看待Microsoft和Abacus用AI解决OF-DFT泛函的问题？和如何理解OF-DFT（Orbital-Free Density Functional Theory）？。

Kohn-Sham方程

“ If you don’t like the answer, change the question.”

Kohn-Sham觉得相互作用体系过于复杂，于是试图将原始的多电子相互作用体系变为更容易求解的辅助系统。Kohn-Sham假设原始系统的基态密度等于某些选定的非相互作用系统的基态密度。由于非相互作用体系是可解的，所以最终的困难和误差会集中在交换-关联泛函的近似上。

考虑辅助系统的哈密顿量：

$$\hat{H}_{aux}=-\frac12 \nabla^2 + V_{eff}^\sigma(\mathbf{r})$$

由于没有相互作用，辅助系统的密度可以写为自旋轨道的平方和：

$$n_{aux}(\mathbf{r}) = \sum_{\sigma}n_{\sigma}(\mathbf{r})=\sum_{\sigma}\sum_{i=1}^{N_{\sigma}}|\psi_{i\sigma}(\mathbf{r})|^2$$

独立粒子的动能为：

$$T_{s}[\rho[\psi]] = -\frac12\sum_{\sigma}\sum_{i=1}^{N_{\sigma}}\langle\psi_{i\sigma}|\nabla^2|\psi_{i\sigma}\rangle$$

总能量为：

$$E_{KS}[\rho[\psi]] = T_{s}[\rho[\psi]] + \int d\mathbf{r}V_{ext}(\mathbf{r})n(\mathbf{r})+E_H[\rho]+E_{II}[\rho]+E_{xc}[\rho]$$

其中，$E_{xc}$是交换-关联能，定义为由于平均场近似和轨道动能近似导致的能量误差：

$$E_{xc} = T-T_s +E_{ee}-E_H$$

对总能量做变分，得到Kohn-Sham方程：

$$(\hat H_{KS}^\sigma-\epsilon_i^\sigma)\psi_{i\sigma}(\mathbf{r})=0$$

其中，$\hat H_{KS}^\sigma$是有效哈密顿量：

$$\begin{aligned} \hat H_{KS}^\sigma &= -\frac12\nabla^2 + V_{ext}(\mathbf{r})+V_H(\mathbf{r})+V_{xc}(\mathbf{r})\\ &=-\frac12\nabla^2 + V_{eff}(\mathbf{r}) \end{aligned}$$

唯一和波函数有关的动能近似项变成了算符，这意味着给定电子密度，我可以算出有效势，然后求解Kohn-Sham方程得到波函数。

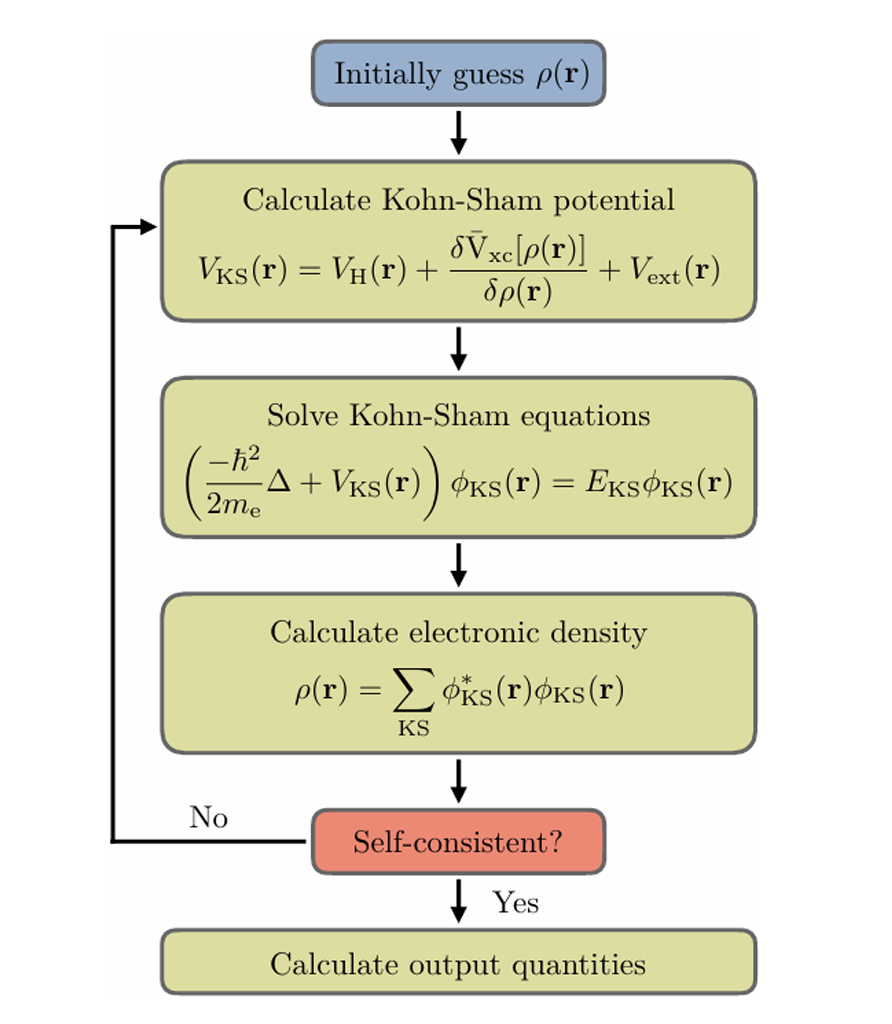
KSDFT的流程

• 猜测初始的电子密度$n(\mathbf{r})$，计算有效势$V_{eff}(\mathbf{r})$；
• 用$V_{eff}(\mathbf{r})$计算Kohn-Sham方程，得到新的波函数和密度；
• 用新的密度计算新的有效势，直到收敛。

在近似交换-关联泛函时，有不同的近似方程，组成了KSDFT的雅各比天梯：

• 第一级：局域密度近似（LDA, Local Density Approximation）,交换能是局域电子密度的函数 $$E_\mathrm{xc}^\mathrm{LDA}[n]=\int n(\mathbf{r})\epsilon_\mathrm{xc}(n(\mathbf{r}))d\mathbf{r}$$
• 第二级：广义梯度近似（GGA, Generalized Gradient Approximation），交换能还是局域电子密度梯度的函数，更加普遍可以把任意阶的导数作为变量，这种方法无法考虑长程相互作用的影响。 $$E_\mathrm{xc}^\mathrm{GGA}[n]=\int n(\mathbf{r})\epsilon_\mathrm{xc}(n(\mathbf{r}),\nabla n(\mathbf{r}))d\mathbf{r}$$
• 第三级：meta-GGA（Meta-Generalized Gradient Approximation），交换能密度还是局域动能密度的函数 $$E_\mathrm{xc}^\mathrm{meta-GGA}[n]=\int n(\mathbf{r})\epsilon_\mathrm{xc}(n(\mathbf{r}),\nabla n(\mathbf{r}),\tau(\mathbf{r}))d\mathbf{r}$$ 其中动能密度$\tau(r)$由KS方程确定的轨道波函数确定 $$\tau(r)=\sum\limits_i|\nabla\psi_{i}(r)|^2$$
• 第四级：杂化泛函（Hybrid Functionals）（exact exchange and compatible correlation），引入了精确交换能，杂化泛函的形式为 $$E_{xc}^{hybrid}=E_{xc}^{GGA}+a(E_{x}^{exact}-E_{x}^{GGA})$$ 这里的精确交换能定义为： $$\begin{aligned} E_{x}&=\int\mathrm{dr}n(\mathbf{r})\varepsilon_{x}(\mathbf{r}), \\ n(\mathbf{r})\varepsilon_{x}(\mathbf{r}) & =-\frac{1}{2}\sum_{\sigma}\int\mathrm{dr}^{\prime}\frac{|\rho_{\sigma}(\mathbf{r},\mathbf{r}^{\prime})|^{2}}{|\mathbf{r}-\mathbf{r}^{\prime}|}, \\ \rho_{\sigma}(\mathbf{r},\mathbf{r}^{\prime}) & =\sum_{\alpha}\Theta(\mu-\varepsilon_{\alpha\sigma})\psi_{\alpha\sigma}^{*}(\mathbf{r})\psi_{\alpha\sigma}(\mathbf{r}^{\prime}) \end{aligned}$$
• 第五级： exact exchange and exact partial correlation,引入了Gorling- Levy second-order correlation energy