金属电子论

• Drude的经典金属模型
  • 电导
  • 霍尔效应
  • 热导
  • 总结
• Sommerfeld的量子金属模型
  • 零温下的费米能
  • 非零温下的电子化学势和比热
    • 费米-狄拉克积分
    • 化学势
    • 比热容
  • 泡利顺磁性
  • 金属的反射率

忽略电子电子相互作用和电子离子相互作用，是金属电子论的主要近似。Drude大胆地将气体模型引入了电子的描述，而Sommerfeld则在此基础上引入了量子统计（费米-狄拉克统计）。

Drude的经典金属模型

Drude作出如下假设：

• 独立电子近似：忽略电子与电子之间的相互作用；
• 自由电子近似：除碰撞外，忽略电子和离子的相互作用（感受不到周期势场）；
• 弛豫时间近似：电子与离子的碰撞满足泊松过程；
• 通过碰撞来达到局域热平衡，且碰撞后速度与碰撞前速度无关。

假设弛豫时间为$\tau$，在外场$\vec{F}$作用下，电子有$(1-\dfrac{dt}{\tau})$的概率不发生碰撞，有$\dfrac{dt}{\tau}$的概率发生碰撞（由于速度的随机分布，平均动量为0），则Drude模型中电子的运动方程为：

$$\vec{p}(t+dt)=(1-\frac{dt}{\tau})[\vec{p}(t)+\vec{F}dt]+0\times\frac{dt}{\tau}$$

化简得到：

$$\frac{d\vec{p}}{dt}=\vec{F}-\frac{\vec{p}}{\tau}$$

Drude模型中电子在电场、磁场和温度梯度场中的运动可以导出宏观电导、霍尔效应和热导。

电导

$$\frac{d\vec{p}}{dt}=-e\vec{E}-\frac{\vec{p}}{\tau}$$

解得：

$$\vec{p}(t)=\vec{p}(0)e^{-\frac{t}{\tau}}-\tau e\vec{E}$$

平衡后，电子的速度为：

$$\vec{v}_D=-\frac{\tau e\vec{E}}{m}$$

电流密度为：

$$\vec{J}=-ne\vec{v}_D=\frac{n\tau e^2}{m}\vec{E}=\sigma\vec{E}$$

从而可以导出电导：

$$\sigma=\frac{n\tau e^2}{m}$$

实验测得的电导在高温时有着较好的近似，但在低温情况下偏差较大，这是因为弛豫时间随温度有很大的变化。一个与弛豫时间无关的模型是霍尔效应。

显然，按照这一经典理论，由于电子的动能与温度正比，因此速度与温度的关系为：

$$\vec{v}_D\propto \sqrt{T},\quad \tau \propto T^{-1/2}\Rightarrow \sigma\propto T^{-1/2}$$

我们将在后续谈到这一关系是实验错误的。

霍尔效应

$$\frac{d\vec{p}}{dt}=-e\vec{E}-\frac{e\vec{p}}{m}\times\vec{B}-\frac{\vec{p}}{\tau}$$

令$\frac{d\vec{p}}{dt}=0$，得：

$$\vec{E}=-\frac{\vec{p}}{m}\times\vec{B}-\frac{\vec{p}}{e\tau}$$

将动量表示为电流：

$$\vec{p}=m\vec{v}_D=-\tau e\vec{E}=-m\vec{J}/ne$$

代入得到：

$$\vec{E}=\frac{1}{ne}\vec{J}\times\vec{B}+\frac{1}{\sigma}\vec{J}$$

定义霍尔系数为：

$$R_H=-\frac{1}{ne}$$

实验中，一价金属符合得很好，但是其他价态区别很大，有的是负数，有的甚至小了很多个数量。这是因为Drude模型从根本上是非量子的，这在下面的Sommerfeld模型中会得到改进。

热导

电子在温度梯度场中不受到外场力，因此需要从统计的角度分析。考虑从$x\pm L$运动到$x$的电子，考虑电子携带的能量是温度的函数，那么热流为：

$$J_Q=\frac{1}{2}nv_F[\varepsilon(T(x-L))-\varepsilon(T(x+L))]$$

化为微分方程：

$$J_Q=-nv_F^2\tau\frac{d\varepsilon}{dT}\frac{dT}{dx}$$

考虑三维情况，速度均方为原来的三分之一：

$$J_Q=-\frac{1}{3}nv_F^2\tau c_v\nabla T$$

由热导的定义得到：

$$\kappa=\frac{1}{3}\tau v_F^2 c_v$$

代入$c_v=\frac{\pi^2}{2}n k_B (\frac{T}{T_F})=\frac{\pi^2}{2}n k_B (\frac{k_BT}{\frac12 mv_F^2})$得到：

$$\kappa=\frac{\pi^2}{3} \frac{\tau n k_B^2T}{m}$$

洛伦兹数定义为：

$$L=\frac{\kappa}{\sigma T}=\frac{\pi^2}{3}(k_B/e)^2$$

是一个和材料性质无关的常数，实验中符合得很好。

总结

物理量	电导率 $\sigma$	霍尔系数 $R_H$	热导率 $\kappa$	磁化率 $\chi$
公式	$\sigma=\dfrac{n\tau e^2}{m}$	$R_H=-\dfrac{1}{ne}$	$\kappa=\dfrac{1}{3}\tau v_D^2 c_v$	$\chi=n\mu^2\beta\mu_0$

Sommerfeld的量子金属模型

Drude模型解释了欧姆定律，但其局限从实验上看，在于：

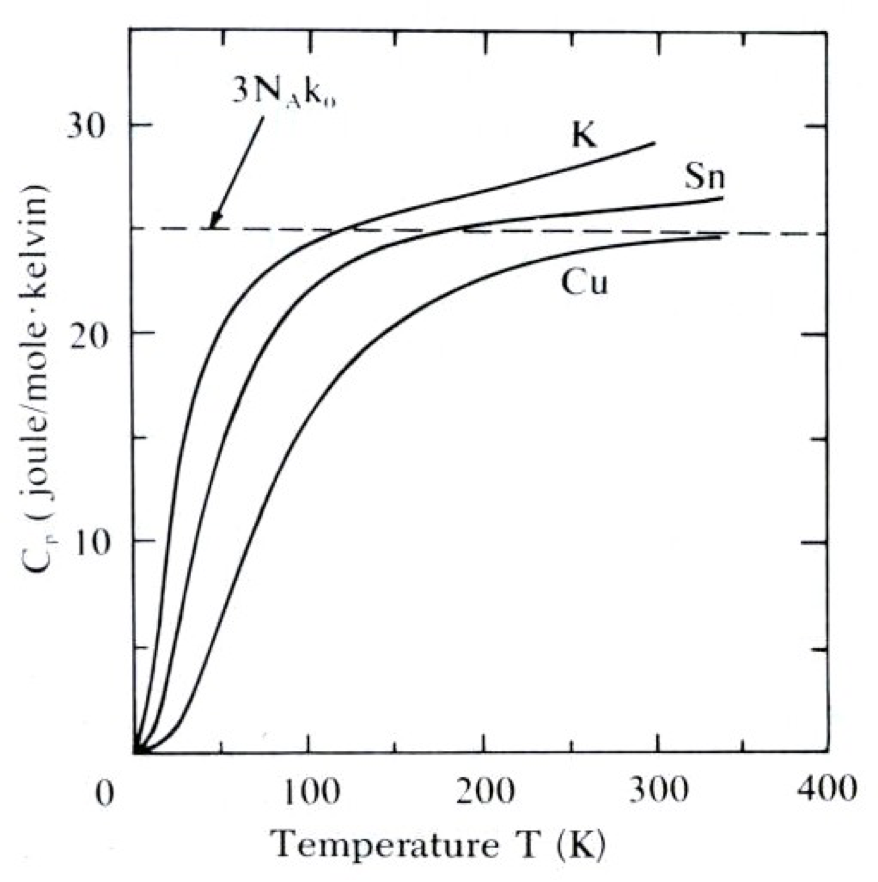
• 无法解释电子的热容极小的问题，根据经典理论，其热容达$\frac{3}{2}k_B$（实际只有1%量级），但整个晶体也就$3k_B$（爱因斯坦模型）；
• 无法解释金属的电导率随温度的变化规律，经典理论认为电导率$\sigma\propto T^{-1/2}$，但实验中发现$\sigma\propto T^{-1}$；
• 无法解释电子的顺磁性随着温度的变化而变化。

从理论上看，Drude模型认为电子的碰撞是频繁的，且忽略了晶体对电子的作用。Sommerfeld认为在势场的约束下，电子得到约束，反而更加自由。

Sommerfeld沿用了Drude的两个假设，并对碰撞假设进行了修正：

• 独立电子近似：忽略电子与电子之间的相互作用；
• 自由电子近似：忽略电子和离子的相互作用；
• 不碰撞假设：电子不但不与电子碰撞，也不与离子碰撞；
• 费米狄拉克分布：由于电子是费米子，遵循费米-狄拉克统计。

Sommerfeld模型“让电子更加自由”。

零温下的费米能

由费米统计可知：

$$f(E)=\frac{1}{e^{\frac{E-\mu}{k_BT}}+1}$$

当$T=0$的时候，分布函数存在突变：

$$f(E)=\begin{cases} 1, & E<\mu \\ 0, & E>\mu \end{cases}$$

突变点为电子的化学势$E_F=\mu$，也称为费米能。现在的问题是如何确定费米能的数值。

考虑三维电子气，最高能级的量子数和电子的个数存在以下关系：

$$2\times\frac{1}{8}\times\frac{4}{3}\pi m_F^3=N\rightarrow m_F=\sqrt[3]{\frac{3N}{\pi}}$$

相应的费米能为：

$$E_F=m_F^2\frac{\pi^{2}\hbar^{2}}{2mL^{2}}=\frac{\hbar^{2}}{2m}(3n\pi^2)^{\frac23}$$

其中$n=\frac{N}{L^3}$。

该基态的总能量为：

$$E_{tot}=\int_0^{m_F} E_F(m_F)\frac18(4\pi m_F^2)dm_F =\frac15 \frac{\pi^{3}\hbar^{2}}{2mL^{2}} m_F^5=\frac{3}{5}E_FN$$

电子气的零温压强为：

$$P=\frac23\frac{E_{tot}}{V}=\frac23\frac{3}{5}E_Fn=\frac{2}{5}E_Fn$$

零温下的费米能其实就是化学势，但是当温度升高时，化学势会发生变化。

用分布函数表示的话：

$$N=\int_0^{\infty}N(E)f(E)dE=\int_0^{E_F}N(E)dE$$

其中$N(E)=\frac{L^3}{2\pi^2}(2m/\hbar)^{3/2}E^{1/2}$（曾在近独立粒子的最概然分布中自由粒子的微观状态描述中得到了证明）。最终得到：

$$N=\frac{L^3(2m/\hbar)^{3/2}}{3\pi^2}E_F^{3/2}$$

总的能量为：

$$E_{tot}=\int_0^{E_F}E N(E)dE=\frac{L^3(2m/\hbar)^{3/2}}{5\pi^2}E_F^{5/2}=\frac35E_FN$$

这种方法更为简洁。

相应地，费米能对应的波矢为：

$$k_F=\frac{m_F\pi}{L}=\sqrt[3]{3\pi^2 n}$$

费米能是电子占据与否的分界线，类比于声子的德拜频率（对于的德拜波矢）：

$$k_D=\sqrt[3]{6\pi^2 n}$$

系数的差别源于电子可以在一个轨道上占据两个态，而声子只能占据一个。

非零温下的电子化学势和比热

费米-狄拉克积分

非零温下的分布函数不再是阶跃函数，但仍然近似满足：

$$f(E)=\frac{1}{e^{\frac{E-\mu}{k_BT}}+1}=\begin{cases} 1, & E\ll\mu \\ 1/2,& E\approx\mu \\ 0, & E\gg\mu \end{cases}$$

我们将在下面用到费米狄拉克积分：

$$F_{l}(\eta)=\int_0^{\infty}\frac{x^{l}}{e^{x-\eta}+1}dx$$

在$\mu \gg k_BT$下，可以做以下渐进展开：

$$F_{l}(\eta)\approx \frac{\eta^{l+1}}{l+1}+\frac{l\pi^2}{6}\eta^{l-1}+\cdots$$

对于$l=1/2$的情况，费米狄拉克积分为：

$$F_{1/2}(\eta)\approx \frac23\eta^{3/2}(1+\frac{\pi^2}{8}\eta^{-2}+\cdots)$$

对于$l=3/2$的情况，费米狄拉克积分为：

$$F_{3/2}(\eta)\approx \frac{2}{5}\eta^{5/2}(1+\frac{5\pi^2}{8}\eta^{-2}+\cdots)$$

化学势

和上面的思路一样，我们先通过电子总数的积分式来确定化学势：

$$N=\int_0^{\infty}N(E)f(E)dE=\int_0^{\infty}\frac{N(E)}{e^{\frac{E-\mu}{k_BT}}+1}dE$$

其中$N(E)=\frac{L^3}{2\pi^2}(2m/\hbar)^{3/2}E^{1/2}$。

引入无量纲量：$x=\frac{E}{k_BT},\eta=\frac{\mu}{k_BT}$，则有：

$$N=\frac{L^3(2m/\hbar)^{3/2}}{2\pi^2}(k_BT)^{3/2}\int_0^{\infty}\frac{x^{1/2}}{e^{x-\eta}+1}dx$$

从中发现了费米狄拉克积分：

$$F_{1/2}(\eta)=\int_0^{\infty}\frac{x^{1/2}}{e^{x-\eta}+1}dx$$

在低温极限$\eta\gg 1$下，费米狄拉克积分近似为：

$$F_{1/2}(\eta)\approx \frac23\eta^{3/2}(1+\frac{\pi^2}{8}\eta^{-2}+\cdots)$$

所以：

$$N=\frac{L^3(2m/\hbar)^{3/2}}{3\pi^2}\mu(T)^{3/2}(1+\frac{\pi^2}{8}\eta_F^{-2})$$

反解得到：

$$\begin{aligned} \mu(T)&=\mu(0)(1+\frac{\pi^2}{8}\eta_F^{-2})^{-2/3}\\ &\approx \mu(0)(1-\frac{\pi^2}{12}\eta_F^{-2})\\ &\approx \mu(0)(1-\frac{\pi^2}{12}\eta_F^{-2}|_{T=0})\\ \end{aligned}$$

引入费米温度$T_F=\mu(0)/k_B$，最终得到：

$$\mu(T) = \mu(0)\left[1 - \frac{\pi^2}{12}(\frac{k_BT}{\mu(0)})^2\right]=\mu(0)\left[1 - \frac{\pi^2}{12}(\frac{T}{T_F})^2\right]$$

比热容

对能量积分：

$$E_{tot}=\int_0^{\infty}E N(E)f(E)dE=\frac{L^3(2m/\hbar)^{3/2}}{2\pi^2}(k_BT)^{5/2}\int_0^{\infty}\frac{x^{3/2}}{e^{x-\eta}+1}dx$$

使用费米狄拉克积分展开：

$$F_{3/2}(\eta)\approx \frac{2}{5}\eta^{5/2}(1+\frac{5\pi^2}{8}\eta^{-2}+\cdots)$$

得到：

$$\begin{aligned}E_{tot}&=\frac25\frac{L^3(2m/\hbar)^{3/2}}{2\pi^2}\mu^{5/2}(T)(1+\frac{5\pi^2}{8}\eta_F^{-2})\\ &=\frac35 \mu^{-3/2}(0)\mu^{5/2}(T)(1+\frac{5\pi^2}{8}\eta_F^{-2})\\ &=E_{tot}(0)\frac{\mu^{5/2}(T)}{\mu^{5/2}(0)}(1+\frac{5\pi^2}{8}\eta_F^{-2})\\ &=E_{tot}(0)\left[1 - \frac{\pi^2}{12}(\frac{T}{T_F})^2\right]^{5/2}(1+\frac{5\pi^2}{8}(\frac{T}{T_F})^{2})\\ &=E_{tot}(0)\left[1 + \frac{5\pi^2}{12}(\frac{T}{T_F})^2\right] \end{aligned}$$

以及电子的比热容：

$$C_V =\frac{\partial E_{tot}}{\partial T}= E_{tot}(0)\ \frac{5\pi^2}{6}\frac{T}{T_F^2} = \frac{\pi^2}{2}N k_B (\frac{T}{T_F})$$

费米温度的量级大概在$10^4\sim 10^5 K$，远高于室温$300K$，这就可以解释化学势偏离很小，而电子比热大概为$\frac32k_B$的1%量级。总的来说，这是因为只有费米面附近$k_BT$的电子受到的激发，对比热有所贡献。

电子气体的一些结论：

物理量	费米波矢 $k_F$	费米速度 $v_F$	费米能 $E_F$	化学势 $\mu$	比热容 $C_V$
公式	$k_F=\sqrt[3]{3\pi^2 n}$	$v_F=\frac{\hbar k_F}{m}$	$E_F=\frac{\hbar^2 k_F^2}{2m}$	$\mu(T)\approx \mu(0)(1-\frac{\pi^2}{12}(\frac{T}{T_F})^2)$	$C_V\approx \frac{\pi^2}{2}N k_B (\frac{T}{T_F})$

晶体是由声子和电子两种准粒子组成的，作以下表格对比：

	电子	声子
统计	费米-狄拉克	玻色-爱因斯坦
截至波矢	$k_F=\sqrt[3]{3\pi^2 n}$	$k_D=\sqrt[3]{6\pi^2 n}$
低温极限热容	$C_V\approx \dfrac{\pi^2}{2}N k_B (\dfrac{T}{T_F})$	$C_V\approx \dfrac{12\pi^4}{5}Nk_B(\dfrac{T}{\Theta_D})^3$
高温极限热容	$C_V\approx \dfrac32Nk_B$	$C_V\approx 3Nk_B$

可以发现两个现象：

• 在低温时，电子对晶体热容的贡献更大；高温时，声子贡献是电子的两倍；
• 高温近似下$\dfrac12$系数的差别源自能均分定理（见 玻尔兹曼统计 ），声子每个自由度有两个平方项（动能和势能），所以会多一倍。

低温下金属的比热可以写成：

$$C_V=\gamma T+\beta T^3$$

实验中测量的结果$\gamma_{exp}$和自由电子气给出的结果比较接近，但对于多价金属差别很大。

泡利顺磁性

在 玻尔兹曼统计 中，我们曾讨论了顺磁性固体由于磁矩和外磁场耦合导致的磁性变化，即居里定律：

$$M=n\mu^2\beta H$$

其中$\chi=n\mu^2\beta\mu_0$。这说明磁化率和温度成反比。然而实验中得到的低温极限下的金属磁化率近似为常数，在室温下，约为经典值的$1\%$。

实际上，对磁化强度有贡献的电子依然来自费米面的附近的电子。没有外磁场时，电子的正反磁矩比例相同，随着外场的逐渐增加，磁矩方向相反的电子能量升高，会跃迁到能量较小的“顺磁态”，这部分的电子数目为：

$$\frac{1}{2}N(E_F)\mu_B B$$

磁矩反转$2\mu_B$，带来的磁化强度为：

$$M=2\mu_B\times\frac{1}{2}N(E_F)\mu_B B=\mu_B N(E_F)\mu_B B=\mu_B^2 N(E_F) B$$

相应的磁化率为：

$$\chi=\frac{\mu_0 M}{B}=\mu_0\mu_B^2 N(E_F)$$

是一个常数，正比于态密度。

金属的反射率

自由电子气模型由于类似等离子体行为，可以通过计算等离子体的本征频率：

$$\omega_p^2=\frac{ne^2}{\epsilon_0 m},\hbar \omega_p\approx 3eV$$

解释低频可见光波段（$\hbar\omega_p\approx 5\sim 15eV$）下金属的高反射率，以及高频光下的穿透行为。但由于模型太简单，无法解释不同金属的不同的光泽。

金属电子论所有不尽人意的地方，如金属的光泽，霍尔系数的偏差，电导的偏差，电子的比热，会在Bloch电子的运动和输运现象进行描述。