晶格动力学
简谐近似
我们在绪论中提到,在绝热近似下,晶格的哈密顿量为:
这仍然是一个多体问题,为了解决它,我们通常会引入简谐近似。记势能项为$V(\{\vec{R}_n\})$,在平衡位置$\{\vec{R}_n^0\}$附近展开:
记微扰为$\vec{q}_n=\vec{R}_n-\vec{R}_n^0$,平衡位置的势能项和一阶导为零,则势能项可以写成:
简正模和格波
简正模理论
考虑哈密顿量为:
由正则方程$\dot{p}_i=-\frac{\partial H}{\partial q_i}$,我们可以得到:
解这个方程是困难的,不过我们可以使用正交变换,将3n个原子坐标变为简正坐标,具体可见 小振动 :
其中$\vec{Q}$是简正坐标,$\Omega^2$是简正频率的平方矩阵:
这样,正则方程给出:
格波
现在我们解系数关于位置的函数。考虑:
假设:
那么:
这意味着:
同时:
解得:
得到的这个类波解被称为格波,只在格点的原子上有定义。不难发现,这其实就是把bloch定理应用到晶格振动上,这里用$\vec{q}$区分电子波矢$\vec{k}$。
量子统计描述
可以直接将上述经典理论过渡到量子理论:
可以分离变量,每一项都是一个谐振子哈密顿量,所以整个系统的本征能量为:
声子是格波的量子,其能量本征值为:
对于声子,其量子数$n_{q,s}$是由波矢$\vec{q}$和模式$s$共同决定的。
系统的总能量为:
运用统计力学的方法,先计算系统的正则配分函数。使用 系综理论 中的结论,系统的正则配分函数等于各个模式的子配分函数的乘积:
准粒子
作为一种准粒子,声子并不携带物理动量。以一维单原子链为例,其动量为:
显然,在非零模式下,粒子动量相互抵消,这也是显然的;零模式下,对应着晶体的平移,当然这不属于粒子本身的动量。
不过,我们考虑外界粒子和晶体的相互作用时,可以引入准动量来保证内部波矢的守恒(比如一个非弹性的光子散射):
一维单原子链的振动
考虑原子间的作用力(简谐近似):
考虑平移对称性:
只考虑相邻原子的相互作用(最近邻假设),运动方程可以写成:
将格波解$u_l=A\exp{(qla-\omega t)}$代入:
其中$q$是波矢。

格波特性:
- 周期性:可以看到频谱是倒空间的周期函数,且$q$和$q+K_h$代表了同一简正模:
- 频谱成带状结构:
一般限制波矢在一个倒格子元胞内。
- 长波极限或连续介质极限:取$q\rightarrow0$,得到退化色散关系:
以上解考虑的是无穷长原子链,然而实际的晶体是有限的,通过考虑周期性边界条件,玻恩-冯卡门条件可以等效为一个无限长原子链中传播的波。
显然对波矢有一定的限制:
这意味着,一维单原子链中的独立波矢数为元胞的个数,波矢的密度为:
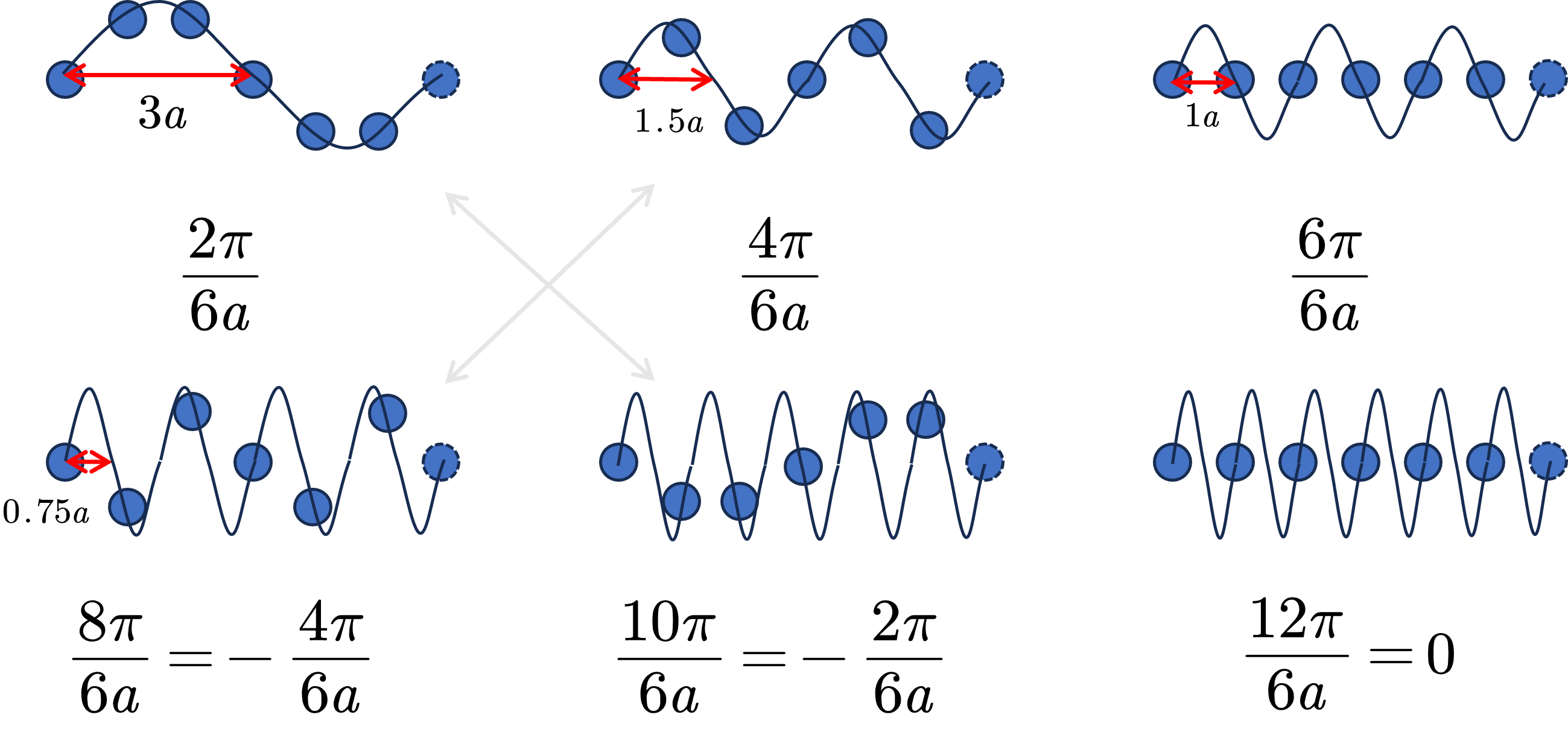
举个例子,6个原子组成的单原子链使用周期边界条件解出的波矢为:
分别对应了以$3a,1.5a,1a,0.75a,0.6a,0.5a$为半周期的波,其中实际上只有3种不等价的波,如下图所示:
具有$q\rightarrow 0,\omega(q)\rightarrow 0$的简正模被称为声学模,对应的色散关系被称为声学支。
一维双原子链振动
简谐近似加上最近邻假设:
带入格波解$u_l=A\exp(iqla-\omega t),v_l=B\exp(iqla-\omega t)$:
轻重原子的振幅比为:

注意到这里有正负两个解,分别命名为光学支和声学支。
对于声学支,当$q\rightarrow0$时:
这意味着轻重原子的相位和振幅相同(微扰,一起振动),且表现为长波弹性波。
对于声学支,当$q\rightarrow\frac{\pi}{a}$时:
这意味着重原子振动,而轻原子不动。
对于光学支,当$q\rightarrow0$时:
这意味着轻重原子的相位相反(反向振动),而质心不动。
对于光学支,当$q\rightarrow0$时:
这意味着轻原子振动,而重原子不动。
格波的性质:
- 周期性:$\omega_\pm(q)=\omega_\pm(q+K_h)$
- 频谱:$\omega<\sqrt{\frac{2\beta}{m_1}},\sqrt{\frac{2\beta}{m_2}}<\omega<\sqrt{\frac{2\beta}{\mu}}$
- 退化为单原子链:$m_1=m_2$时:
- 独立波矢数等于元胞数;独立模式数等于自由度数(原子个数)。
三维晶格振动
对于N个元胞的晶体,假设每个元胞中含有n个原子,那么总自由度是3nN,也就是说独立的模式数为3nN。对于n个不同的原子,可以列出3n个运动方程,其中有3个声学支和3n-3个光学支。其中$\frac13$是纵波,另外$\frac23$是横波。
我们刚刚推导的单原子链和双原子链只谈论了纵波,所以只表现出一支声学支。
一个波矢对应了3n个不同的频率,那么状态数(state)$s=1,2,\cdots,3n$,对应的频率为$\omega_s(q)$。同时,在每一个模式上可以取N个不同的波矢(格波),因此总的状态数为$3nN$,刚好等于晶体的总自由度。
晶体的热学性质

以上是实验测得的固体的热容曲线。我们将逐步对其的性质进行解释。
我们回顾一下电子的热容是怎么计算的(传送门: 金属电子论 ):
- 通过$N=\int_0^{\infty}N(E)f(E)dE$,计算电子的化学势随温度的变化;
- 通过$E_{tot}=\int_0^{\infty}E N(E)f(E)dE$,计算电子的总能量随温度的变化;
- 对温度求导,得到热容$C_V=\frac{\partial E_{tot}}{\partial T}$。
晶格(声子)的热容和电子的区别很大,主要体现在:
- 声子是玻色子,遵循玻色-爱因斯坦分布;电子是费米子,遵循费米-狄拉克分布;
- 声子的化学势为0,电子的化学势随温度变化;
- 声子的理论积分需要在第一布里渊区内进行,而电子(气体)的积分需要在整个波矢空间上进行。
当然,他们存在许多共同点:
- 在温度很低的时候,声子的积分截止到德拜波矢,而电子的积分截止到费米波矢;
- 积分中,分别出现了费米狄拉克积分和玻色爱因斯坦积分;
晶体的热容描述
考虑声子作为玻色子占据:
统计物理指出,热容可以写成:
其中$x=\dfrac{\hbar\omega_s(q)}{k_BT}$。
理想气体极限
考虑高温极限,即$x\rightarrow0$,此时热容为:
和实验测得的热容一致,是一个常数。
极低温近似
极低温下,无法激活光学支的声子,只有声学支的声子被激活,此时可以假设频率正比于波矢的大小:
将对$\vec{q}$的求和变为准连续的积分,并扩展到全波矢空间(该操作带来的误差极小):
引入平均声速$\bar{v}$:
利用积分公式:
得到:
中间温度
当温度不满足极低温近似时,我们无法将积分扩展到全空间(此时的误差很大)。有两种近似办法:爱因斯坦模型和德拜模型。
爱因斯坦模型
爱因斯坦假设只存在一种频率$\omega$,因此:
当$x\rightarrow\infty$时,热容为:
这当然是一个很粗糙的模型,除了能够定性说明热容趋于0外,并不能给出定量趋近速度。
德拜模型
德拜在此基础上,做出了以下修正:
- 不再假设频率固定,但是只考虑三支长声学支的低频声子,且忽略他们的差别$\omega(q)\approx v|\vec{q}|$:
将对布里渊区的积分改为对德拜球的积分。
其中,德拜比热容函数定义为:
德拜频率可以由模式密度积分给出。模式密度为:
总模式数为3N,则:
德拜温度定义为:
德拜理论在极低温下趋近于上述低温近似的结果,同样给出了$T^3$的依赖关系。德拜模型在中间温度下也能给出较好的拟合。
对于复式晶格,非低温近似会导致光学支也有声子激发,一个较好的方法是利用德拜模型近似声学支,用爱因斯坦模型近似光学支。
其中,$p$是光学支的个数,$\Theta_E$是光学支的德拜温度。爱因斯坦模型的比热容函数为:
声子态密度
类似 能带论 中提到的电子的态密度,声子态密度为:
由于$\omega_s(\vec{q})$在倒格子空间的周期性,在某些地方会出现van Hove奇点(van Hove singularity)$\nabla_{\vec{k}}\omega_s(\vec{q})=0$。
当使用德拜近似的时候,等频面的面积为$S_\omega=4\pi(\omega/v)^2$,因此:
非简谐效应
简谐近似将晶格的振动处理为独立的谐振子,这意味着:
- 声子之间没有相互作用,即热导是无穷大的;
- 声子在抛物线势阱下振动,平均值为平衡位置,无法解释热膨胀。
准简谐近似指的是当非简谐效应较小的时候,仍然可以使用简谐近似来处理晶格振动,而将非简谐效应作为微扰来处理。
热膨胀
要想计算晶体的体膨胀系数:
引入体积弹性模量:
得到:
而要想计算压强随温度的关系,就需要计算自由能:
自由能可以通过配分函数计算:
因此,压强计算为:
该公式仅与$\left(\frac{\partial \omega_s}{\partial V}\right)_T$有关,而频率只依赖于原子质量和相互作用力:
这一项刚好在简谐近似下消失了。
格林艾森对上述式子进行了简化:
热传导
在准简谐近似下的框架下,非简谐效应作为微扰引起了声子态之间的跃迁。总的来说,声子的跃迁满足以下两个守恒律:
- 能量守恒:$\sum_{q,s}\hbar\omega_s(q)n_{q,s}=\sum_{q’,s’}\hbar\omega_{s’}(q’)n_{q’,s’}$
- 动量守恒:$\sum_{q,s} q n_{q,s}=\sum_{q’,s’} q’ n_{q’,s’}+\vec{K}_h$
声子的热导可以借助气体热导公式来讨论:
分三种情况来分类讨论。
高温近似
温度极高的时候$T\gg \Theta_D$,声子被大量激发,占据数近似为:
也就是说声子数目正比于温度,那么声子碰撞的弛豫时间满足
此时热容近似常数,所以热导近似为:
低温近似
低温下$T\ll \Theta_D$,必须要有$\vec{K}_h$介入,意味着声子的波矢应该与$\vec{q}_D$相近(此时声子的波矢方向反向,相当于热阻很大)。此时声子占据数近似为:
也就是说声子碰撞的弛豫时间满足:
此时热容在极低温时近似为:
所以在极低温下,热导近似为:
在较低温度下,热导近似为: