晶格及其平移对称性

晶体结构

几种常见的晶体结构：

简单立方晶体结构(simple cubic structure,sc)

体心立方晶体结构(body-centered cubic structure,bcc)

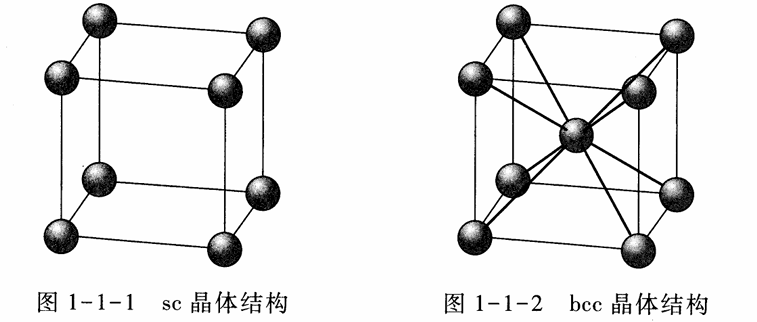
面心立方晶体结构(face-centered cubic structure,fcc)

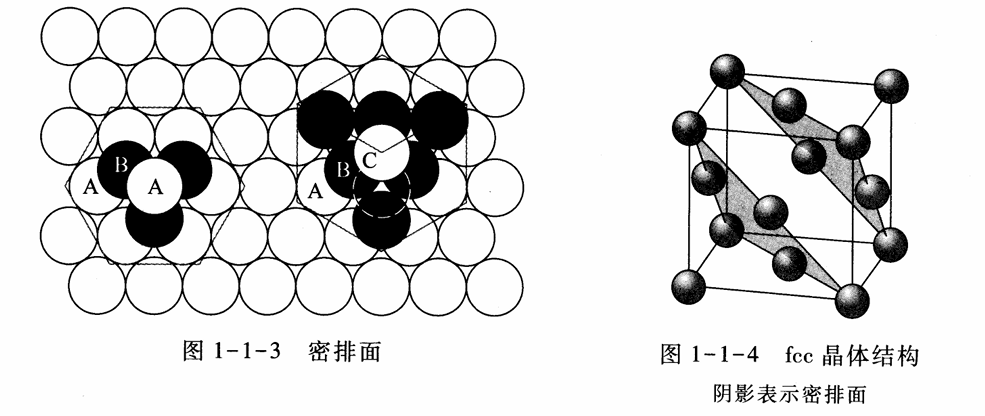
六角密堆积晶体结构(hexagonal close-packed structure,hcp)

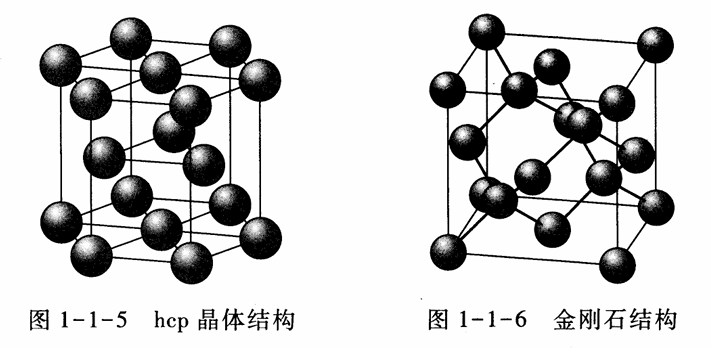
金刚石结构(diamond structure)

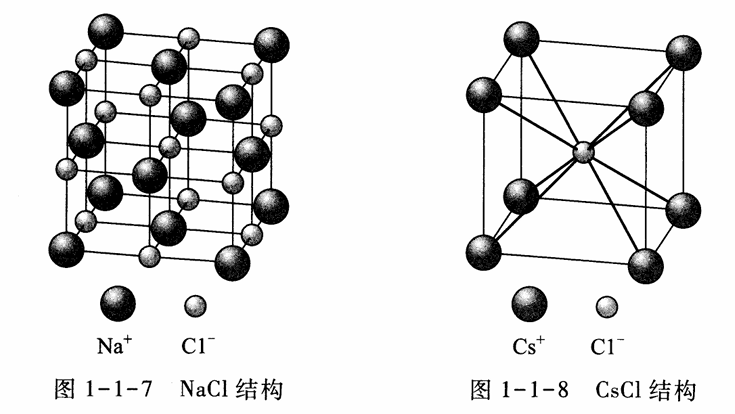
NaCl结构

CsCl结构

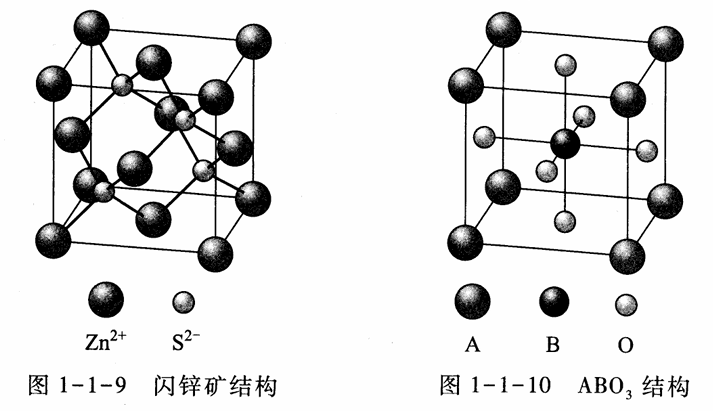
闪锌矿结构

钙钛矿结构

晶体结构	原子数	配位数	原子堆积率	常见例子
sc	1	6	0.52	极少
bcc	2	8	0.68	碱金属
fcc	4	12	0.74	贵金属
hcp	6	12	0.74	二价金属，碱土金属
diamond	8	4	0.34	金刚石和硅
NaCl	2	6	0.74	碱金属卤化物
CsCl	2	8	1.00
ZnS	4	4	0.64
CaTiO3	5	12	0.74

晶格的数学描述

$\vec{R_l}=l_1\vec{a_1}+l_2\vec{a_2}+l_3\vec{a_3},\forall l_i \in Z$

该矢量可以描述点阵中的所有结点。数学上，还可以用空间密度函数描述点阵：

$\rho(\vec{r})=\sum_{l_1,l_2,l_3} \delta(\vec{r}-\vec{R}_l)$

初基元胞

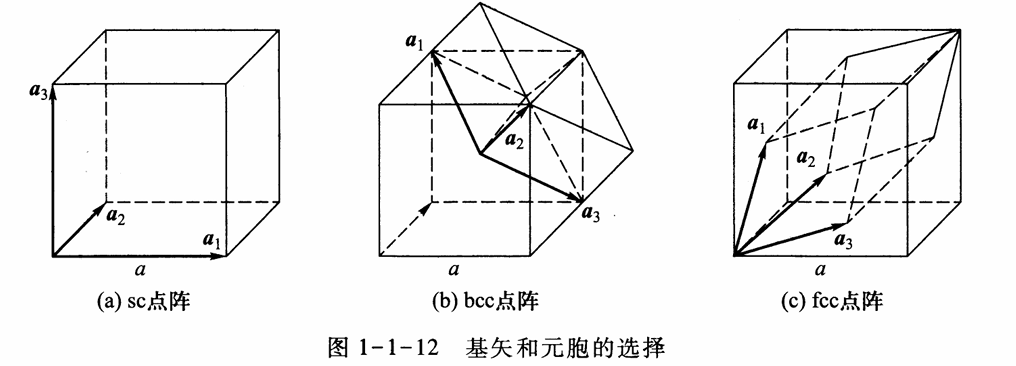
基矢的选择不是唯一的，但所构成的平行六面体的体积是不变的。对于基矢构成的元胞，有公认的元胞——初基元胞。

sc：
$\vec{A}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}=a\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ $V=|\vec{A}|=a^3$
bcc：
$\vec{A}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}=\frac{a}{2}\begin{pmatrix}-1&1&1\\1&-1&1\\1&1&-1\end{pmatrix}$ $V=|\vec{A}|=\frac{a^3}{2}$
fcc：

$\vec{A}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}=\frac{a}{2}\begin{pmatrix}0&1&1\\1&0&1\\1&1&0\end{pmatrix}$ $V=|\vec{A}|=\frac{a^3}{4}$

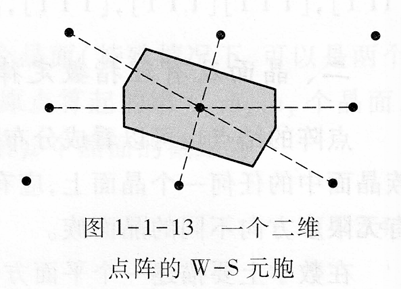
维格纳-塞茨(Wigner-Seitz)元胞

结点在胞的中间，且到胞的边界的距离最近（中心结点与最近邻和次近邻原子连线的中垂面构成了W-S元胞的边界）。

晶列和晶面

晶列

平移矢量中，$[l_1l_2l_3]$是晶体的晶向指数。以$\bar{l_i}$表示负数。

晶面

用晶面的三个截距$(h_1h_2h_3)$来描述晶面，显然，如果只关心晶面的方向，三个数中只有两个是独立的。一般选取$h_1,h_2,h_3$为互质整数。

倒点阵

在实空间内，正点阵表示为：

$\rho(\vec{r})=\sum_{l_1,l_2,l_3} \delta(\vec{r}-\vec{R}_l)$

在傅里叶空间内，倒点阵可以表示为：

$\rho(\vec{k})=\sum_{k_1,k_2,k_3} \delta(\vec{k}-\vec{K}_h)$

其中：

$\vec{k}_i=\frac{2\pi\epsilon_{ijk}}{\Omega}(\vec{a}_j\times\vec{a}_k)$ $\vec{K}_h=h_1\vec{b}_1+h_2\vec{b}_2+h_3\vec{b}_3$

倒点阵具有以下性质：

正倒点阵基矢正交：
$\vec{a}_i\cdot\vec{b}_j=2\pi\delta_{ij},\vec{A}\vec{B}^T=2\pi\vec{I}$
正倒点阵体积：
$\Omega^*=\vec{b}_1\cdot(\vec{b}_2\times\vec{b}_3)=\frac{(2\pi)^3}{\Omega}$

晶体的宏观对称性

对称操作

定义正交变化矩阵$\vec{A}$，如果满足晶体在该变化下不变，那么称该变化为对称操作。

显然，对称操作总是旋转操作和中心对称的组合。

旋转操作：$\vec{A}=\begin{pmatrix}1&0&0\\0& \cos\theta & -\sin\theta \\0& \sin\theta & \cos\theta \end{pmatrix},|\vec{A}|=1$；

中心对称：$\vec{A}=\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{pmatrix},|\vec{A}|=-1$。

对称素

对称元素就是一个物体借以进行对称操作的一根轴、一个平面和一个点：

如果一个物体绕某轴旋转 $\frac{2\pi}{n}$ 及其倍数保持不变，则称这个轴为$n$次旋转轴，记为$n$；
如果一个物体对某点反演不变，称为这点为反演中心，记为$i$；
如果一个物体绕某轴旋转$\frac{2\pi}{n}$后，再反演，最终不变，称为 $n$次旋转反演轴（象转轴），记为 $\bar{n}$。

平移对称性对宏观对称性的限制

考虑旋转对称性，平移对称性要求单种密铺正多边形，即：

点：$\theta=0,1\& \bar{1}$
线：$\theta=\frac{2\pi}{2},2\& \bar{2}$
三角形：$\theta=\frac{2\pi}{6},6\& \bar{6}$
四边形：$\theta=\frac{2\pi}{4},4\& \bar{4}$
六边形：$\theta=\frac{2\pi}{3},3\& \bar{3}$

将$\bar{2}$记为$m$；有的对称素由其他的对称素组合成$\bar{3}=3+i$，$\bar{6}=3+m$。

总的来说，晶体的宏观对称性只具有8种独立的对称素：1，2，3，4，6，i，m，$\bar{4}$。

对称素的组合规则

两个2次轴的夹角只能是$30^\circ,45^\circ,60^\circ,90^\circ$

证明：依次绕着两个2次轴旋转，等效于一个$2\theta$的旋转，所以$\theta$只能是$30^\circ,45^\circ,60^\circ,90^\circ$。

晶体不能有多于一个6次轴，也不可能有一个6次轴和一个4次轴相交

证明：如果有一个n次轴和一个m次轴相交，首先经过n次轴产生了$\theta=\frac{n-2}{n}\pi$的正n边形内角，此内角还可以通过m次轴形成凸多面体，则：

$m(\frac{n-2}{n})\pi\leq 2\pi$

代入$n=6,m=6$和$n=6,m=4$，得到矛盾。此条件应该是必要条件。

简单晶体结构的对称素

立方对称结构（sc,bcc,fcc）
- 三个4次轴，$3\times3=9$个对称操作
- 四个3次轴，$4\times2=8$个对称操作
- 六个2次轴，$6\times1=6$个对称操作
- 一个不动操作。

加上反演，一共有48个对称操作。

正四面体对称
- 三个4次反演轴，$3\times3=9$个对称操作
- 四个3次轴，$4\times2=8$个对称操作
- 六个2次反演轴，$6\times1=6$个对称操作
- 一个不动操作。

一共有24个对称操作。

六角对称
- 一个6次轴，$1\times5=5$个对称操作
- 三个2次轴，$3\times1=3$个对称操作
- 三个2次轴，$3\times1=3$个对称操作
- 一个不动操作。

加上反演，一共有12个对称操作。

晶体点阵和结构的分类

晶体点群

$C_n$循环群：$n$次旋转轴
- $C_{nh}$：$n$次旋转轴加上与旋转轴垂直的镜面；
- $C_{nv}$：$n$次旋转轴加上与旋转轴平行的镜面；
$S_{2n}$：
- n是偶数：$2n$次旋转反演轴，与$C_{2n}$同构；
- n是奇数：$n$次旋转反演轴，与$C_{n}$同构；
$D_n$（二面体群）：$n$次旋转轴和n根垂直于这根主轴的二重轴；
- $D_{nh}$：加上与旋转轴垂直的镜面；
- $D_{nd}$：加上n个与旋转轴平行的镜面；
$T$（四面体群）：12个纯转动操作
- $T_d$：24个对称操作
- $T_h$：加上中心反演
$O$（八面体群）：24个纯转动操作
- $O_h$：48个对称操作

表格：

晶系	点群
三斜晶系	$C_1,S_2$
单斜晶系	$C_2,C_{2h},C_s$
正交晶系	$D_2,C_{2v},D_{2h}$
三角晶系	$C_3,C_{3i},D_3,C_{3v},D_{3d}$
四方晶系	$C_4,C_{4h},C_{4v},D_4,D_{2d},D_{4h},S_4$
六方晶系	$C_6,C_{6h},C_{3v},C_{3h},D_6,D_{2h},D_{6h}$
立方晶系	$T,T_h,T_d,O,O_h$

晶体结构及其平移对称性