晶体的结合

晶体中原子的聚集是原子间相互作用的结果，这种使原子发生聚集的强烈的相互作用就是化学键。考虑波恩近似，一个两原子体系的能量为：

$$E=\frac{p_1^2}{2m}+\frac{p_2^2}{2m}+\frac{q_1q_2}{4\pi\epsilon_0 r}+E_{R}$$

其中，$E_R$是电子的能量。在两原子相互靠近时，不仅会受到核间的库伦斥力，价电子的重新排布也会影响作用力$-\dfrac{\partial E(R)}{\partial R}$。价电子的重新分布情况取决于原子本身束缚电子的能力，所以，我们以下首先介绍原子本身束缚电子的能力——电负性。

原子的负电性

Mulliken考虑使用原子的电离能(ionization energy)和电子亲和能(electron affinity)来定义原子的电负性：

$$\chi=\frac{K_m}{2}(I+E_A)$$

其中，$I$是原子的电离能，$E_A$是原子的电子亲和能。$K_m$是一个常数，通常使得Li的电负性为1.0。除此之外，还有Pauling、Allen等人提出的电负性定义。

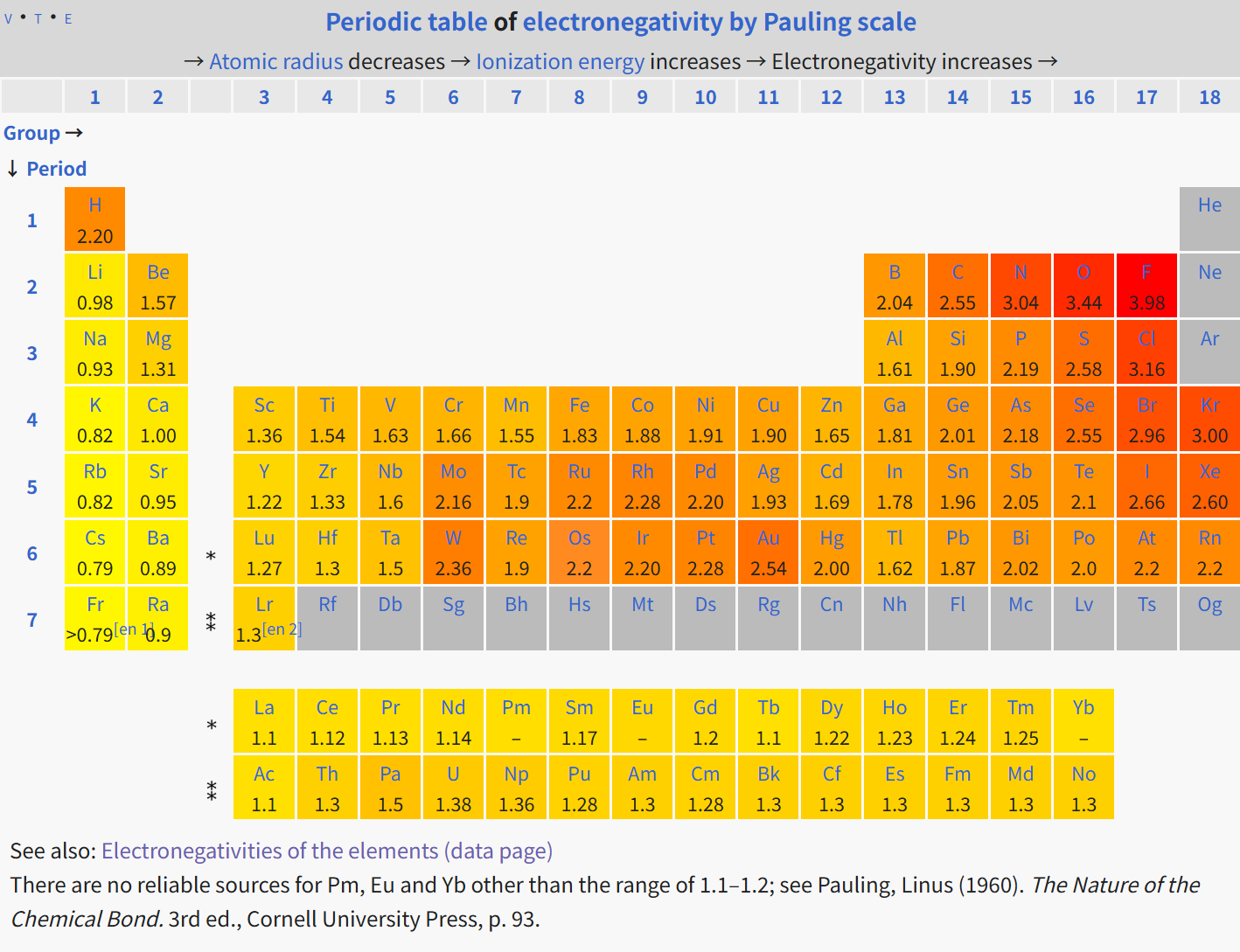
电离能定义为原子失去一个电子所需的能量。亲合能定义为原子获得一个电子所释放的能量。随着核电子数的增加，原子核正电的作用增加比外部电子层的平均负电作用快，导致同一周期内的原子电离能逐渐增大。

晶体结合的类型

金属键

金属原子对电子的束缚能力较弱，价电子进而呈现退局域化的特征，从而导致能量降低。用以下图像可以形象地理解金属键的形成。考虑若干无穷势阱中的电子，其能量为：

$$E_{tot}=kE_n=k\frac{n^2\hbar^2\pi^2}{2mL^2}$$

当无穷势阱间的壁垒被打破：

$$E_{tot}'=k\langle E_{n}\rangle=k\frac{n^2\hbar^2\pi^2}{2m(kL)^2}$$

尽管由于泡利不相容原理，电子的能级会相应升高，其总能量会降低。

由于金属晶体中价电子的公有化，可以抽象为负电子云中的正电荷离子实系统。若金属的体积减小，电子云的密度增大，导致库伦能降低，同时电子云的动能会增大，二者的平衡决定了金属的体积。

共价键

对于负电性较强的元素，电子既不会像金属中退局域化那样自由移动，也不会像离子化合物中那样完全转移。相反，电子会在两个原子之间共享，形成共价键。共价键的形成伴随能量降低，可以用量子力学的全同粒子与交换力来理解。自旋反平行的态由于空间波函数对称，存在等效吸引力，可以存在与排斥力平衡的状态。

也可以理解为单态位于低势能区的概率密度要更大，所以能量更低。

考虑以下图像：两个无穷深势阱中的电子，其能量为：

$$E_{tot}=2E_1=k\frac{\hbar^2\pi^2}{2mL^2}$$

如果两个无穷深势阱的壁垒被打破，对称态的能量为：

$$E_{tot}'=E_1'=k\frac{\hbar^2\pi^2}{2m(2L)^2}$$

反对称态的能量为：

$$E_{tot}''=E_1''=k\frac{2^2\hbar^2\pi^2}{2m(2L)^2}>E_{tot}'$$

sp3杂化

金刚石的基态原子组态为$1s^2 2s^2 2p^2$，为什么能形成四个共价键？这是因为在基态时，$2s$和$2p$轨道会发生杂化，形成四个未配对的电子$\phi_{2s},\phi_{2p_x},\phi_{2p_y},\phi_{2p_z}$，然后四个波函数重新组合为：

$$\Phi_1=\frac12(\phi_{2s}+\phi_{2p_x}+\phi_{2p_y}+\phi_{2p_z})$$ $$\Phi_2=\frac12(\phi_{2s}+\phi_{2p_x}-\phi_{2p_y}-\phi_{2p_z})$$ $$\Phi_3=\frac12(\phi_{2s}-\phi_{2p_x}+\phi_{2p_y}-\phi_{2p_z})$$ $$\Phi_4=\frac12(\phi_{2s}-\phi_{2p_x}-\phi_{2p_y}+\phi_{2p_z})$$

尽管杂化需要能量，但由于形成的四个共价键的能量更低，杂化是有利的。

离子键

当两个负电性差异很大的原子靠近时，电子会从负电性较弱的原子转移到负电性较强的原子上，形成离子键。离子键可以理解为极性共价键的极端情况。

范德瓦耳斯键

中性原子没有很强的相互作用力，但是量子涨落引起的瞬时电偶极矩会产生等效的吸引力。相比于其他类型的结合（一个电子伏特量级），范德瓦耳斯键的结合能较小，通常在0.1eV左右。

可以通过以下图像解释其六次方反比的吸引势。两组正负电荷分别通过弹簧耦合，中间相邻的为异种电荷。不考虑库伦相互作用，基态能量为：

$$E_{tot}=-\hbar\omega_0,\quad \omega_0=\sqrt{\frac{k}{m}}$$

考虑相互作用的哈密顿量：

$$\Delta H=\frac{e^2}{r}+\frac{e^2}{r-x_1+x_2}-\frac{e^2}{r+x_2}-\frac{e^2}{r-x_1}$$

其中，$x_1$和$x_2$是两组原子之间的距离，$r$是同种电荷之间的距离。通过泰勒展开，可以得到：

$$\Delta H\approx -\frac{2e^2x_1x_2}{r^3}$$

引入简正坐标：

$$\begin{cases} x_+=\dfrac{x_1+x_2}{\sqrt2}\\ x_-=\dfrac{x_1-x_2}{\sqrt2} \end{cases}$$

振动能量变为：

$$H=\frac{1}{2}(k-\frac{2e^2}{r^3})x_+^2+\frac{1}{2}(k+\frac{2e^2}{r^3})x_-^2$$

本征能量为：

$$E_{tot}'=\frac12\hbar(\omega_++\omega_-)=\frac12\hbar\sqrt{\frac{k-\frac{2e^2}{r^3}}{m}}+\frac12\hbar\sqrt{\frac{k+\frac{2e^2}{r^3}}{m}}\propto \frac{A}{r^6}$$

氢键

尽管氢拥有一个价电子，但由于第一电离能大于其他碱金属元素，很难形成离子键。在一定条件下，可以和电负性强的原子形成共价键，裸露的原子核再跟另一个原子形成氢键。

以水为例，氧$2s^2 2p^4$形成了不等性$sp^3$杂化，其中两个轨道为共价键，两个轨道跟氢原子形成氢键。氢键的结合能较小，通常在0.1eV左右。

混合键

以石墨为例，碳$2s^2 2p^2$形成了$sp^2$杂化，三个杂化波函数分别为：

$$\Phi_1=\frac1{\sqrt{3}}(\phi_{2s}+\sqrt2\phi_{2p_x})$$ $$\Phi_2=\frac1{\sqrt{6}}(\sqrt2\phi_{2s}+\sqrt3\phi_{2p_x}-\phi_{2p_y})$$ $$\Phi_3=\frac1{\sqrt{6}}(\sqrt2\phi_{2s}-\sqrt3\phi_{2p_x}-\phi_{2p_y})$$

剩下的一个$2p_z$电子则用于形成金属键，层间则形成范德瓦尔斯键。这可以解释石墨的导电性和层间的滑动性。

这里提一嘴杂化波函数的构造原则：

• 归一化：$|\Phi_i|^2=1$
• 正交性：$|\Phi_i\Phi_j|=\delta_{ij}$