Scattering-Theory

Classic Scattering Theory

Differential Cross Section

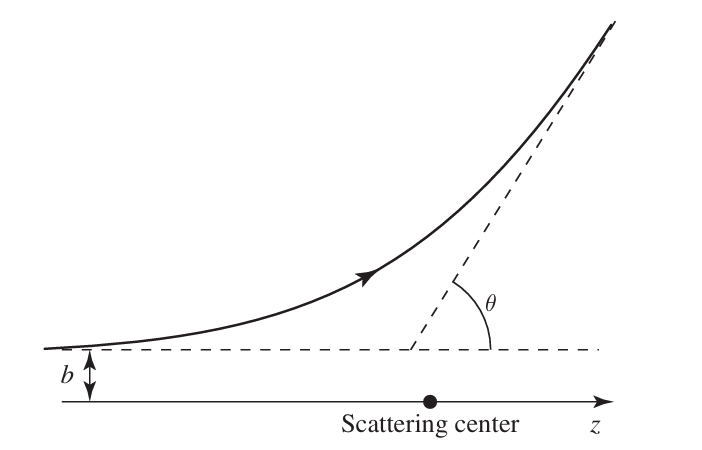
微分散射截面定义为：

$$D(\theta)=\frac{d\sigma}{d\Omega}$$

其中$d\sigma$是单位立体角$d\Omega$内的散射截面。显然，微分散射截面是一个碰撞参数$b$或角度$\theta$的函数。其中：

$$d\sigma =4\pi bdb,d\Omega=4\pi \sin\theta d\theta$$

所以：

$$D(\theta)=\frac{d\sigma}{d\Omega}=\frac{b}{\sin\theta}|\frac{db}{d\theta}|$$

实验上会写为：

$$D(\theta)=\frac{dN/d\Omega}{J}$$

这样分子分母都是可观测量。

Rigid Sphere Scattering

对于刚球，即无限高势垒：

$$b=R\sin{\frac{\theta}{2}}$$

得到：

$$D(\theta)=\frac{R^2}{4}$$

积分得到：

$$\sigma=\pi R^2$$

这和我们的直觉是相符的，即总的散射截面就是球本身截面面积。

Rutherford Scattering

代入：

$$b=\frac{Z_1Z_2e^2}{4\pi\epsilon_0E}\cot{\theta}$$

得到：

$$D(\theta)=\frac{Z_1^2Z_2^2e^4}{4\pi^2\epsilon_0^2E^2}\csc^4{\frac{\theta}{2}}$$

积分发现该积分发散。

Quamtum Scattering Theory

Scattering Amplitude

假设势能不依赖于时间，利用定态微扰理论可以求解散射问题。

对于平面入射波，显然散射前后的平衡态波函数可以写为：

$$\psi(r,\theta,\phi)=A\{e^{ikz}+f(\theta,\phi)\frac{e^{ikr}}{r}\},r\gg 1$$

其中$f(\theta)$是散射振幅。

这个公式是这么来的，先用本征态展开散射部分：

$$\psi(r,\theta,\phi)=A\{e^{ikz}+\sum_{l,m}c_{l,m}\frac{u_l(r)}{r}Y_{l,m}(\theta,\phi)\}$$

无穷远处，$u_l$满足：

$$u_l(r)=e^{ikr}$$

所以：

$$\psi(r,\theta,\phi)=A\{e^{ikz}+\frac{e^{ikr}}{r}\sum_{l,m}c_{l,m}Y_{l,m}(\theta,\phi)\}$$

按照微分散射截面的定义：

$$D(\theta,\phi)=\frac{dN/d\Omega}{J}$$

其中流密度为：

$$J=\frac{\hbar}{m}\Im{(\psi^*\nabla\psi)}=|A|^2\frac{\hbar k}{m}$$

而分子为：

$$\frac{dN}{d\Omega}= \vec{J}_{scatter}r^2=\frac{|A|^2\hbar}{m}\Im{[(f(\theta,\phi)\frac{e^{ikr}}{r})^*\nabla (f(\theta,\phi)\frac{e^{ikr}}{r})]}r^2=|A|^2\frac{\hbar k}{m}|f|^2+O(\frac{1}{r})$$

算得：

$$D(\theta,\phi)=|f(\theta,\phi)|^2$$

Green Function Method

通过格林函数的定义：

$$\frac{\hbar^2}{2m}(\nabla^2+k_i^2)G_0(k_i,\vec{r})=\delta(\vec{r})$$

所以波函数可以通过格林函数表示：

$$\psi(\vec{r})=\phi(\vec{r})+\int_{-\infty}^\infty G_0(k_i,\vec{r}-\vec{r'})V(\vec{r'})\psi(\vec{r'})d\vec{r'}$$

其中$\phi(\vec{r})$满足：

$$\frac{\hbar^2}{2m}(\nabla^2+k_i^2)\phi(\vec{r})=0$$

就是入射波。

这个积分方程的由来是简单的，对左右两边求梯度：

$$\begin{aligned}LHS&=\frac{\hbar^2}{2m}(\nabla^2+k_i^2)\psi(\vec{r})\\RHS&=0+\frac{\hbar^2}{2m}(\nabla^2+k_i^2)\int_{-\infty}^\infty G_0(k_i,\vec{r}-\vec{r'})V(\vec{r'})\psi(\vec{r'})d\vec{r'}\\&=V(\vec{r})\psi(\vec{r})\end{aligned}$$

求格林函数：

$$G_0(k_i,\vec{r}-\vec{r'})=\frac{1}{(2\pi)^3}\frac{2m}{\hbar^2}\int \frac{e^{-i\vec{k}\cdot(\vec{r}-\vec{r'})}}{k_i^2-k'^2}d\vec{k'}=-\frac{m}{2\pi\hbar^2}\frac{1}{|\vec{r}-\vec{r'}|}e^{\pm ik|\vec{r}-\vec{r'}|}$$

取延迟（retarded）项：

$$G_0^+(k_i,\vec{r})=-\frac{m}{2\pi\hbar^2}\frac{e^{ikr}}{r}$$

Operator Form

用算符表示：

$$|\psi^+_p\rangle=|k_i\rangle+\hat G_0^+\hat V|\psi^+_p\rangle$$

迭代法表示出：

$$|\psi^+_p\rangle=|k_i\rangle+\hat G_0^+\hat V|k_i\rangle+\hat G_0^+\hat V\hat G_0^+\hat V|k_i\rangle+\cdots=\sum_n (\hat G_0^+\hat V)^n|k_i\rangle$$

其中算符定义为：

$$\langle r|\hat G_0^+|r'\rangle=G_0^+(\vec{r}-\vec{r'})$$ $$\langle r|\hat V|r'\rangle=V(r)\delta_{r,r'}$$

所以：

$$f(\theta,\phi)=-\frac{4\pi^2m}{\hbar^2}\langle \vec{k_f}|V|\psi^+_p\rangle$$

定义$\hat T$算符为：

$$\hat T^+|k_i\rangle=\hat V|\psi^+_p\rangle$$

那么波恩级数可以写为：

$$\hat T^+=\hat V+\hat V\hat G_0^+\hat V+\hat V\hat G_0^+\hat V\hat G_0^+\hat V+\cdots$$

散射振幅为：

$$f(\theta,\phi)=-\frac{4\pi^2m}{\hbar^2}\langle \vec{k_f}|\hat T^+|k_i\rangle$$

微分散射截面为：

$$D(\theta,\phi)=\frac{(2\pi)^4m^2}{\hbar^4}|\langle \vec{k_f}|\hat T^+|k_i\rangle|^2$$

当$\hat G_0^+\hat V\ll 1$时，可以进行波恩近似：

$$\hat T^+\approx \hat V$$

这时候散射截面为：

$$D(\theta,\phi)=\frac{(2\pi)^4m^2}{\hbar^4}|\langle \vec{k_f}|\hat V|k_i\rangle|^2=\frac{m^2}{(2\pi)^2\hbar^4}|\int e^{i(\vec{k}_i-\vec{k}_f)\vec{r}}V(\vec{r})d\vec{r}|^2$$

格林函数的算符形式：

$$\hat G_0^\pm=\frac{1}{E-\hat H_0\pm i\epsilon}$$

Optical Theorem

光学定理：

$$\frac{k}{4\pi}\sigma_{tot}=\Im [f(\theta=0,\phi=0)]$$

证明：

$$\begin{aligned} \Im{f(\theta=0)}&=\frac{4\pi^2m}{\hbar^2}\Im{\langle \vec{k_i}|\hat T^+|\vec{k_i}\rangle}\\ &=\frac{4\pi^2m}{\hbar^2}\Im{\langle \psi_k|(1-\hat V\hat G_0^-)\hat V|\psi_k\rangle}\\ &=\frac{4\pi^2m}{\hbar^2}\langle \psi_k|\Im{\hat V\hat G_0^-\hat V}|\psi_k\rangle\\ &=\frac{4\pi^2m}{\hbar^2}\langle \psi_k|\hat V\Im{\hat G_0^-\hat V}|\psi_k\rangle\\ &=\frac{4\pi^2m}{\hbar^2}\langle \psi_k|\hat V\Im{\frac{1}{E_0-\hat H-i\epsilon}}\hat V|\psi_k\rangle\\ &=\frac{4\pi^3m}{\hbar^2}\langle \psi_k|\hat V\delta(E-H_0)\hat V|\psi_k\rangle\\ &=\frac{4\pi^3m}{\hbar^2}\langle \psi_k|\hat V\delta(E-H_0)\hat T|\vec{k_i}\rangle\\ &=\frac{4\pi^3m}{\hbar^2}\int\langle \psi_k|\hat V\delta(E-H_0)|\vec{k}'\rangle\langle \vec{k}'|\hat T|\vec{k_i}\rangle d^3k'\\ &=\frac{4\pi^3m}{\hbar^2}\int\langle \psi_k|\hat V|\vec{k}'\rangle\langle \vec{k}'|\hat T|\vec{k_i}\rangle \delta(E-\frac{\hbar^2k'^2}{2m})d^3k'\\ &=\frac{4\pi^3m}{\hbar^2}\frac{m}{\hbar^2k}\int_{|k|=|k_i|}\langle \psi_k|\hat V|\vec{k}\rangle\langle \vec{k}|\hat T|\vec{k_i}\rangle k^2d\Omega\\ &=\frac{4\pi^3m^2}{\hbar^4}k\int_{|k|=|k_i|}|\langle \vec{k}|\hat T|\vec{k}_i\rangle|^2 d\Omega\\ &=\frac{k}{4\pi}(\frac{4\pi^2 m}{\hbar^2})^2\int d\Omega|f(\theta,\phi)|^2\\ &=\frac{k}{4\pi}\sigma_{tot} \end{aligned}$$

Example: Square Well

方势阱的势能为：

$$V(r)=\begin{cases} V_0,&r<a\\ 0,&r>a \end{cases}$$

由散射振幅的定义：

$$f(\theta)=-\frac{m}{2\pi\hbar^2}\int e^{i(\vec{k}-\vec{k'})\cdot\vec{r}}V(r)d\vec{r}=-\frac{2m}{\hbar^2}\int_0^a rV(r)\sin{(qr)}dr$$

其中$|q|=2k\sin\frac{\theta}{2}$，积分得到：

$$f(\theta)=-\frac{2mV_0a}{\hbar^2q^2}[\frac{\sin(qa)}{qa}-\cos{(qa)}]$$

Example: Yukawa Potential