满足定域或非简并条件的粒子系统可以采用玻尔兹曼统计，而不满足非简并条件的系统，需要用玻色-爱因斯坦统计或费米-狄拉克统计处理。

不满足非简并条件的气体叫做简并气体。不同于理想气体，简并气体不满足定域条件。尽管气体之间的距离更大，但是气体粒子本身的波包尺度也更大。同样的道理，固体虽然原子之间间距小，但是波包更小，是定域系统。

粒子的简并情况也有所区别，具体可根据逸度$z=e^{-\alpha}$进行分类：

理想气体（非简并） 理想玻色/费米气体（弱简并） 玻色-爱因斯坦凝聚 光子气体 自由电子气（强简并）
$e^{-\alpha}\ll1$ $e^{-\alpha}\ll1$但不可忽略 $e^{-\alpha}\to 1^{-}$ $e^{-\alpha}= 1$ $e^{-\alpha}\gg 1$

其中，理想气体因为忽略相互作用，所以化学势$\mu$接近0，但我们在下面会讨论如果不忽略其影响会带来什么变化。自由电子气由于其费米能（化学势）远大于$kT$，所以在统计上表现出强简并特性。

热力学统计量表达式

考虑玻色系统，对于巨正则系综，定义巨配分函数：

在系综理论中，我们会推导玻色统计和费米统计的巨配分函数。

系综的平均粒子数：

系综和平均能量：

外界的广义作用力

熵：

巨热力学势：

对于费米系统，巨配分函数：

将玻尔兹曼统计和玻色统计和费米统计对比:

玻尔兹曼统计 玻色统计 费米统计
配分函数 $Z_1 = \sum_l \omega_le^{-\beta\epsilon_l}$ $\Xi = \prod_l (1-e^{-\alpha-\beta\epsilon_l})^{-\omega_l}$ $\Xi = \prod_l (1+e^{-\alpha-\beta\epsilon_l})^{\omega_l}$
平均粒子数 $N = e^{-\alpha}Z_1$ $\langle N \rangle =-\frac{\partial }{\partial \alpha} \ln \Xi$ $\langle N \rangle =-\frac{\partial }{\partial \alpha} \ln \Xi$
平均内能 $U =N(-\frac{\partial}{\partial\beta})\ln Z_1$ $\langle U\rangle =-\frac{\partial }{\partial \beta} \ln \Xi$ $\langle U \rangle = -\frac{\partial }{\partial \beta} \ln \Xi$
外力 $Y -\frac{N}{\beta}\frac{\partial }{\partial y}\ln Z_1$ $\langle Y \rangle =-\frac1\beta\frac{\partial }{\partial y} \ln \Xi$ $\langle Y \rangle =-\frac1\beta\frac{\partial }{\partial y} \ln \Xi$
熵 $S=Nk(\ln Z_1+\beta U)$ $S =k(\ln \Xi + \alpha \langle N \rangle + \beta \langle E \rangle)$ $S =k(\ln \Xi + \alpha \langle N \rangle + \beta \langle E \rangle)$

其实，玻色和费米统计的配分函数比玻尔兹曼“高一阶”（从求和变成连乘可以看出端倪）。对其求对数：

当满足非简并条件时，$e^{-\alpha}\ll 1$，所以可以用泰勒展开：

可以看到，直接化为了玻尔兹曼统计的配分函数。

弱简并理想玻色气体和费米气体

在 玻尔兹曼统计 中，我们计算了理想气体的若干性质，现在我们考虑弱简并的理想玻色气体和费米气体。回顾此前的粒子数计算（用巨正则配分函数统一描述）：

这说明在非简并条件下，$\ln \Xi$对$\alpha$求导只改变符号。

在弱简并环境下就不能忽略：

的近似影响。代入 近独立粒子的最概然分布 中的自由粒子态密度公式，直接写出配分函数的计算公式：

Note：对于玻色气体，如果温度太低，可能会出现$e^{-\alpha}\geq 2.612$的情况，此时玻色-爱因斯坦凝聚会发生，这时候上述式子就会因为$D(\epsilon=0)=0$而不成立。这一点在下一节会讨论。

考虑弱简并条件，我们可以对$\ln (1- e^{-\alpha-\beta\epsilon})$进行泰勒展开：

代入上式，得到：

这里引入理想气体的配分函数$Z_1$，逸度$z$和玻色函数$g_\nu(z)$：

现在，我们可以放心求解各个热力学量了：

进行简单的变换，就是：

同样的道理，可以定义费米函数：

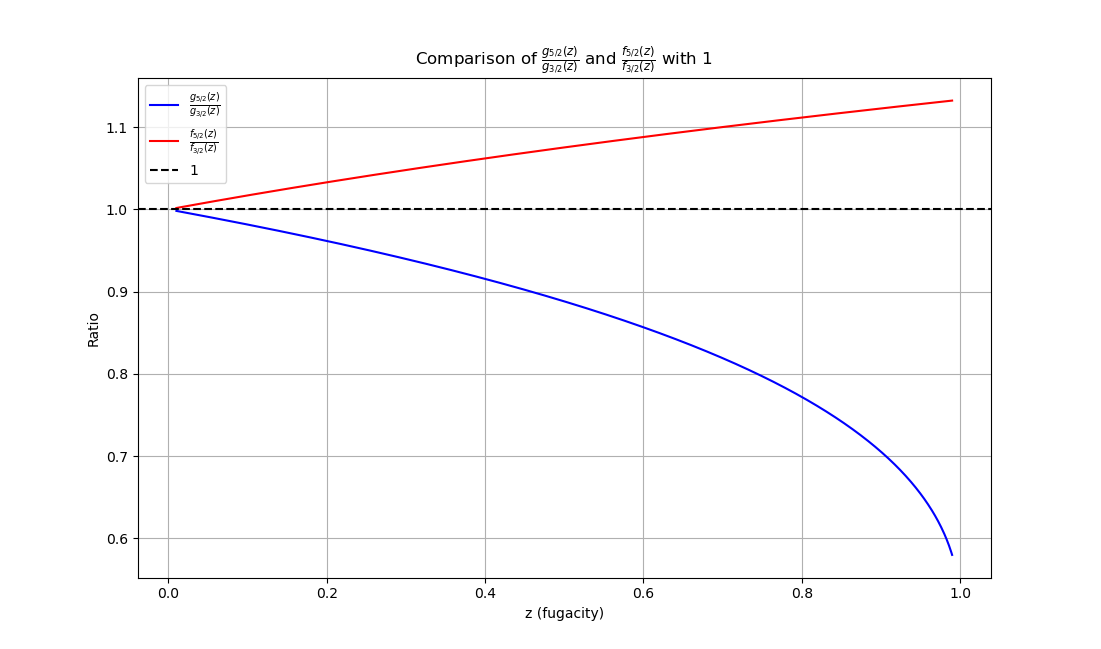
导出费米气体的热力学量，这里不再赘述。显然，费米函数在同阶情况下小于玻色函数。

对比理想气体和理想玻色气体的热力学量：

量 理想气体 理想玻色气体 理想费米气体
配分函数 $Z_1=\dfrac{V}{h^3}\left(\dfrac{2\pi m}{\beta}\right)^\frac32$ $\ln\Xi=Z_1 g_{\frac52}(z)$ $\ln\Xi=Z_1 f_{\frac52}(z)$
$N$ $Z_1e^{-\alpha}=Z_1g_{\infty}(z)$ $Z_1 g_{\frac32}(z)$ $Z_1 f_{\frac32}(z)$
$U$ $\dfrac32 NkT$ $\dfrac32 NkT\dfrac{g_{\frac52}(z)}{g_{\frac32}(z)}$ $\dfrac32 NkT\dfrac{f_{\frac52}(z)}{f_{\frac32}(z)}$
$S$ $k\left(\dfrac52Z_1e^{-\alpha}+\alpha Z_1e^{-\alpha}\right)$ $k\left(\dfrac52Z_1 g_{\frac52}(z) + \alpha Z_1 g_{\frac32}(z)\right)$ $k\left(\dfrac52Z_1 f_{\frac52}(z) + \alpha Z_1 f_{\frac32}(z)\right)$

可以分析，理想玻色气体的内能较理想气体更小，而理想费米气体的内能较理想气体更大，这表明玻色子之间存在等效的吸引作用，而费米子之间存在等效的排斥作用。

alt

import numpy as np
import matplotlib.pyplot as plt

def g_nu(z, nu, n_terms=1000):
    """计算玻色函数 g_nu(z) = sum_{n=1}^∞ z^n / n^nu (级数展开)"""
    n = np.arange(1, n_terms + 1)
    return np.sum(z**n / (n**nu))

def f_nu(z, nu, n_terms=1000):
    """计算费米函数 f_nu(z) = sum_{n=1}^∞ (-1)^{n+1} z^n / n^nu (级数展开)"""
    n = np.arange(1, n_terms + 1)
    return np.sum((-1)**(n + 1) * z**n / (n**nu))

# 定义 z 的范围 (0 < z < 1)
z = np.linspace(0.01, 0.99, 1000)

# 计算 g_{5/2}(z) / g_{3/2}(z)
g_ratio = np.array([g_nu(zi, 5/2) / g_nu(zi, 3/2) for zi in z])

# 计算 f_{5/2}(z) / f_{3/2}(z)
f_ratio = np.array([f_nu(zi, 5/2) / f_nu(zi, 3/2) for zi in z])

# 绘制图形
plt.figure(figsize=(10, 6))
plt.plot(z, g_ratio, label=r'$\frac{g_{5/2}(z)}{g_{3/2}(z)}$', color='blue')
plt.plot(z, f_ratio, label=r'$\frac{f_{5/2}(z)}{f_{3/2}(z)}$', color='red')
plt.axhline(y=1, color='black', linestyle='--', label='1')

plt.xlabel('z (fugacity)')
plt.ylabel('Ratio')
plt.title(r'Comparison of $\frac{g_{5/2}(z)}{g_{3/2}(z)}$ and $\frac{f_{5/2}(z)}{f_{3/2}(z)}$ with 1')
plt.legend()
plt.grid(True)
plt.show()

玻色-爱因斯坦凝聚(BEC)

由上述计算可知：

显然，由于粒子数是守恒的，当温度降低的时候，$Z_1$会变小，而$g_{\frac32}(z)$会变大。遗憾的是，$g_{\frac32}(z)$是有上界$g_{\frac32}(z)\leq g_{\frac32}(1)=\zeta(\frac32)\approx 2.612$的，且当$z>1$的时候，玻色函数发散。这里的原因在上面也提到了，是因为计算配分函数的时候，$\epsilon=0$的态密度为0：

这与玻色分布$a_l=\dfrac{\omega_l}{e^{\alpha+\beta\epsilon_l}-1}(e^{\alpha}\geq1,\mu\leq0)$相违背。

所以当温度降低到某个临界值时，$g_{\frac32}(z)$会达到上限，此时：

当温度继续降低，把配分函数的第一项提取出来：

对其求导得到粒子数：

这里的$N_0$是基态粒子数，$N_{\text{exc}}$是激发态粒子数。由于激发态粒子数目和温度成$N_{\text{exc}}\propto T^{-3/2}$关系，这个式子可以转写为：

所以：

这时候激发态的能量为：

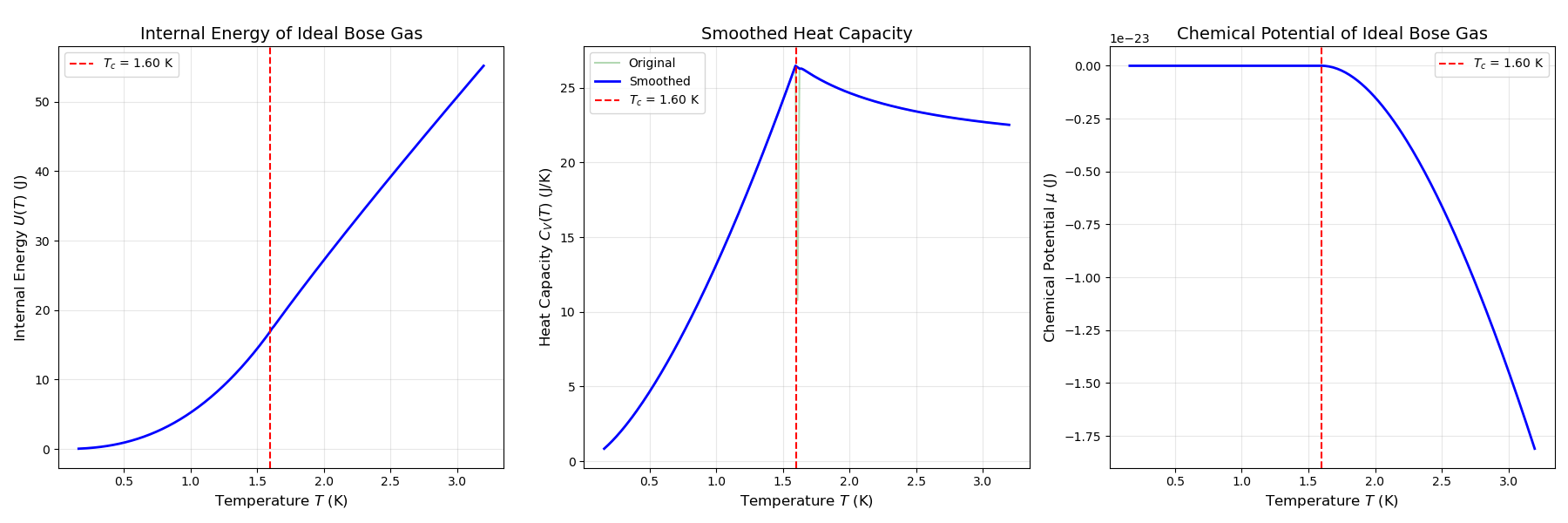
综合大于临界温度的情况，内能表达式为：

热容为（z也是T的函数，所以这里写不出解析的表达式）：

化学势为：

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import zeta
from functools import lru_cache

# 物理常数
h = 6.626e-34       # 普朗克常数 (J·s)
m = 1.67e-27        # 氦原子质量 (kg)
k = 1.38e-23        # 玻尔兹曼常数 (J/K)
N = 1e24            # 总粒子数
V = 1e-3            # 体积 (m³)

# 预计算常数乘积
h2 = h**2
two_pi_mk = 2 * np.pi * m * k
prefactor_Tc = h2 / two_pi_mk
zeta_3_2 = zeta(3/2)

# 计算临界温度 T_c
n = N / V
T_c = prefactor_Tc * (n / zeta_3_2)**(2/3)

# 预计算用于玻色函数的常数
h3 = h**3
two_pi_mk_1_5 = (two_pi_mk)**1.5

# 玻色函数计算（级数展开），使用缓存避免重复计算
@lru_cache(maxsize=1000)
def g_nu(z, nu, n_terms=3000):
    return np.sum(z**np.arange(1, n_terms+1) / np.arange(1, n_terms+1)**nu)

# 缓存已计算的z值
z_cache = {}

# 二分法求解 z(T)，使用缓存
def solve_z(T):
    if T in z_cache:
        return z_cache[T]
    
    Z_1 = (V / h3) * two_pi_mk_1_5 * T**1.5
    left, right = 1e-16, 1 - 1e-16
    for _ in range(200):
        mid = (left + right)/2
        val = Z_1 * g_nu(mid, 1.5) - N
        if abs(val) < 1e-6: 
            z_cache[T] = mid
            return mid
        (left, right) = (left, mid) if val > 0 else (mid, right)
    
    z_cache[T] = (left + right)/2
    return z_cache[T]

# 内能计算，使用缓存
@lru_cache(maxsize=1000)
def U(T):
    if T > T_c:
        z = solve_z(T)
        g_1_5 = g_nu(z, 1.5)
        g_2_5 = g_nu(z, 2.5)
        return 1.5 * N * k * T * g_2_5 / g_1_5
    else:
        return 0.770 * N * k * T * (T/T_c)**1.5

# 数值差分计算热容，使用缓存
def C_V(T, delta_T=1e-4):
    if T > T_c + delta_T:
        return (U(T + delta_T) - U(T - delta_T)) / (2 * delta_T)
    elif T < T_c - delta_T:
        return (U(T + delta_T) - U(T - delta_T)) / (2 * delta_T)
    else:  # 临界区附近
        return (U(T + delta_T) - U(T)) / delta_T

# 化学势计算，使用缓存
@lru_cache(maxsize=1000)
def chemical_potential(T):
    if T <= T_c:
        return 0.0
    else:
        z = solve_z(T)
        return k * T * np.log(z)

# 温度范围
T_range = np.linspace(0.1 * T_c, 2 * T_c, 200)
U_values = [U(T) for T in T_range]
C_V_values = [C_V(T) for T in T_range]
mu_values = [chemical_potential(T) for T in T_range]

# 平滑处理热容曲线
def smooth_spikes(T_range, C_V_values, threshold=1.5):
    C_V_smooth = np.array(C_V_values.copy())
    n = len(C_V_smooth)
    
    derivatives = np.abs(np.diff(C_V_smooth))
    mean_derivative = np.mean(derivatives)
    
    spike_indices = []
    for i in range(1, n-1):
        if (np.abs(C_V_smooth[i+1] - C_V_smooth[i]) > threshold * mean_derivative and
            np.abs(C_V_smooth[i] - C_V_smooth[i-1]) > threshold * mean_derivative):
            spike_indices.append(i)
    
    for i in spike_indices:
        left_val = C_V_smooth[i-1] if i > 0 else C_V_smooth[i]
        right_val = C_V_smooth[i+1] if i < n-1 else C_V_smooth[i]
        C_V_smooth[i] = (left_val + right_val) / 2
    
    return C_V_smooth

C_V_smoothed = smooth_spikes(T_range, C_V_values)

# 绘图
plt.figure(figsize=(18, 6))

# 左子图：内能
plt.subplot(1, 3, 1)
plt.plot(T_range, U_values, 'b-', linewidth=2)
plt.axvline(x=T_c, color='r', linestyle='--', label=f'$T_c$ = {T_c:.2f} K')
plt.xlabel('Temperature $T$ (K)', fontsize=12)
plt.ylabel('Internal Energy $U(T)$ (J)', fontsize=12)
plt.title('Internal Energy of Ideal Bose Gas', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)

# 中子图：热容（平滑后）
plt.subplot(1, 3, 2)
plt.plot(T_range, C_V_values, 'g-', alpha=0.3, label='Original')
plt.plot(T_range, C_V_smoothed, 'b-', linewidth=2, label='Smoothed')
plt.axvline(x=T_c, color='r', linestyle='--', label=f'$T_c$ = {T_c:.2f} K')
plt.xlabel('Temperature $T$ (K)', fontsize=12)
plt.ylabel('Heat Capacity $C_V(T)$ (J/K)', fontsize=12)
plt.title('Smoothed Heat Capacity', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)

# 右子图：化学势
plt.subplot(1, 3, 3)
plt.plot(T_range, mu_values, 'b-', linewidth=2)
plt.axvline(x=T_c, color='r', linestyle='--', label=f'$T_c$ = {T_c:.2f} K')
plt.xlabel('Temperature $T$ (K)', fontsize=12)
plt.ylabel('Chemical Potential $\mu$ (J)', fontsize=12)
plt.title('Chemical Potential of Ideal Bose Gas', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

alt

光子气体

空窖能量守恒，但由于发射和吸收的光子的能量有高低，所以粒子数不守恒，那么拉格朗日法只需要引入一个乘子：

$\alpha=-\frac{\mu}{kT}=0$意味着光子气体的化学势为0。

考虑到光子的自旋量子数为1，所以$\omega_l=2$，光子的态密度为：

考虑到光子的能量关系：

得到：

平均的光子数为：

辐射场的内能为：

这就是普朗克公式。

对于低频情况$\beta \hbar \omega\ll1$：

对于高频情况$\beta \hbar \omega\gg1$：

总的内能为：

内能密度的最大值有：

这就是维恩位移定律。

光子气体的巨配分函数为：

所以内能：

压强：

那么两者的关系：

熵：

金属中的自由电子气体

金属中的自由电子气体是强简并理想费米气体。根据费米-狄拉克分布：

这里考虑了自旋的两个简并。

电子的量子态数为：

平均电子数为：

化学势通过粒子总数求得：

对于0K的电子气：

所以：

解得：

这就是费米能级，令$\mu(0)=\frac{p_F^2}{2m}$，得到费米动量：