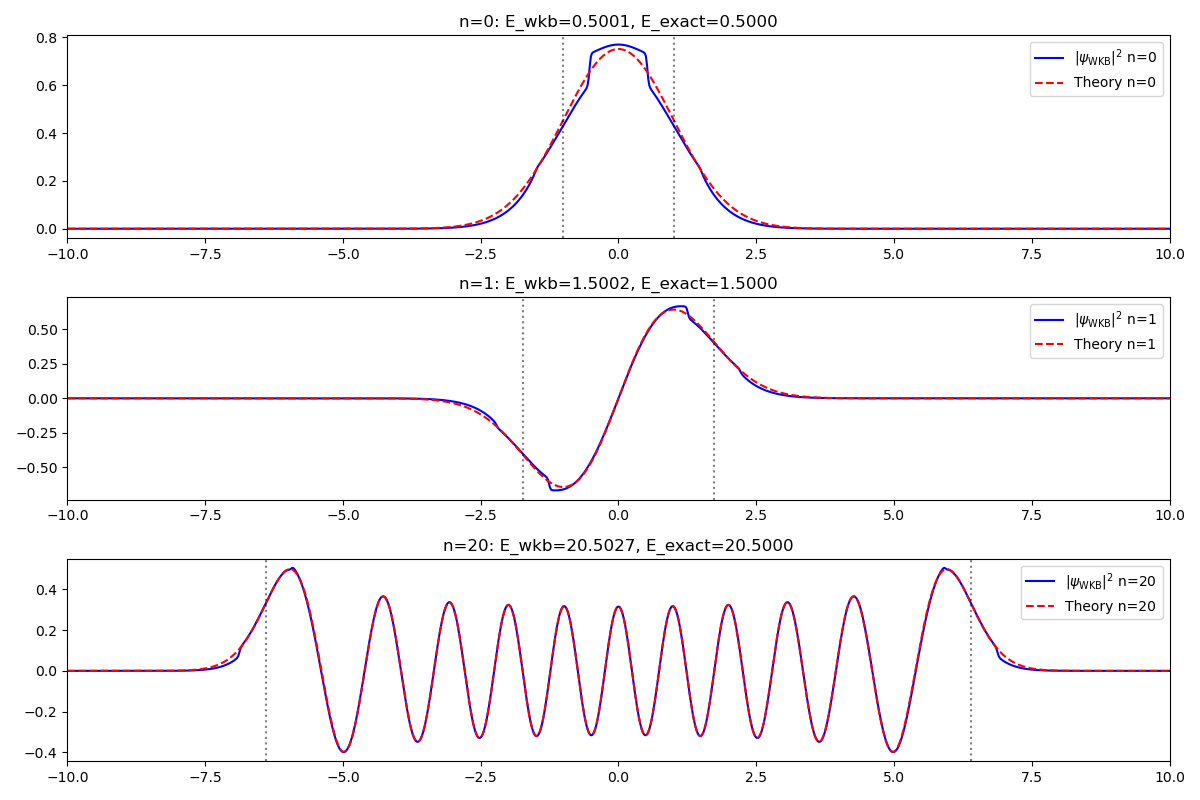
Angular Momentumn and Symmetry
在经典力学中,我们通过类比动量,我们可以推广得到角动量。然而,更深层次的理解需要结合群论和对称性规律来阐释,这也是为什么起这个标题的原因。
转动和角动量对易
有限转动和无穷小转动
我们在之前的学习就知道有限转动是不对易的,这意味着先进行哪个操作影响最后的结果。
我们可以写出有限转动的转动矩阵:
但如果我们计算无穷小转动,可以得到:
量子力学的无穷小转动
我们知道动量算符是平移算符的生成元:
哈密顿算符是演化算符的生成元:
同样地,角动量算符是旋转算符的生成元:
D源自德语Drehung,意为转动。
从经典力学的$R$矩阵到量子力学的$\hat D(R)$算符,假设其具有相同的性质,比如其对易性质,有:
化简得到:
推广得
群论和李代数
群的基本概念
群是一种代数结构,它是一个集合,集合中的元素之间有一种二元运算,满足封闭性、结合律、单位元、逆元。
一个群$G$就是一个集合$\{X,Y,\cdots\}$与这个集合中任意两个元素中的某种运算$\cdot$。满足以下条件:
- Closure: $G\cdot G\in G$
- Associativity: $X\cdot (Y\cdot Z)=(X\cdot Y)\cdot Z$
- Unitarity: $I\cdot X=X=X\cdot I,I\in G$
- Invertibility: $X\cdot X^{-1}=I=X^{-1}\cdot X,X^{-1}\in G$
对于物理来说,这四个性质代表了:
- 系统不变性:在一定操作后系统仍然在群内,即不变;
- 系统操作的顺序性:按照顺序操作的系统与操作的顺序无关;
- 幺正性:什么都不做,系统不变;
- 可逆性:通过相反的操作可以使系统变回来。
如果操作的顺序可以颠倒,那么这个群就是阿贝尔群,即:
- Abel: $X\cdot Y=Y\cdot X$
在物理中,平移操作的群是阿贝尔的,但是旋转不是,就是因为不对易性。
二维群
O(2) Group
保持向量长度不变的操作构成了$O(2)$群,即:
旋转和镜像翻转都是其中的元素:
O取自orthogonal,O(2)的基底是正交归一的,所以才有如上的性质。
SO(2) Group
保持向量长度不变且手性不变的操作构成了$SO(2)$群,即:
这是显然的,因为在线性代数中就讲到$\det{A}=-1$相当于翻转。
S取自special,是特殊的O(2)群。
U(1) Group
保持复数模不变的操作构成了$U(1)$群,即:
U取自Unitary,代表矩阵是幺正的。
我们发现为了描述二维旋转,需要定义复数的概念:
为了和SO(2)的表示相结合,我们定义:
对这两个单位的线性组合描述了二维旋转,且满足:
U(1)和SO(2)是同构的,即$U(1)\cong SO(2)$。但是$\phi=\theta$并不是普遍的关系,我们在下面会谈到。
三维群
SO(3) Group
绕三条旋转轴的旋转矩阵为:
U(2) Group
按照同样的定义,我们可以得到:
一般表示为:
SU(2) Group
一般表示为:
我们也可以从四元数的定义去理解:
其中:
可惜的是,$SU(2)$和$SO(3)$虽然是同构的,即$SU(2)\cong SO(3)$,但是其中的角度旋转并不相同,为$\theta=2\phi$。这不禁让我们想到之前对旋量的操作,的确如此。
自旋1/2系统与有限转动
自旋角动量是$SU(2)$对称性的反应,而轨道角动量是$SO(3)$的对称性的反应。
基本作用力和对称性
基本作用力
| 基本作用力 | 作用范围 | 无量纲量 | 交换粒子 | 群 |
|---|---|---|---|---|
| 引力 | 长程力 | $\alpha_{gravity}=10^{-38}$ | 引力子(graviton) | / |
| 电磁力 | 长程力 | $\alpha=\frac{1}{137}$ | 光子(photon) | U(1) |
| 弱相互作用力 | 短程力 | $\alpha_{weak}=10^{-14}$ | W/Z | SU(2) |
| 强相互作用力 | 短程力 | $\alpha_{strong}=1$ | 胶子(gluon) | SU(3) |
对称性
- 连续对称性
- 空间平移对称性
- 空间旋转对称性
- 时间平移对称性
- 离散对称性
- 空间宇称对称性
- 时间反演对称性
- 电荷共轭对称性
- 规范“对称性”
保系统对称性的操作叫做对称变换,满足:
即:
对称性和简并度
满足系统不变的对称变换有:
如果对称变换是厄密算符:
这必然会导致能级的简并,因为:
对称性和守恒律
考虑无穷小变换
满足幺正条件:
所以:
意味着$\hat F$是厄密算符,所以对应了一个可观测量。如果这时候要求$\hat Q$是对称变换,即:
那么由Ehrenfest定理,$\hat F$是守恒的。
氢原子的四维旋转对称
哈密顿量属于任意本征值的本征子空间都有其对称性群的不可约表示。
什么意思呢,以氢原子的n=2能级为例,有四个本征态:
其对应的旋转矩阵是可分块对角化的,这与上面违背了,这说明我们关于旋转的对称性认知还不完整。
从龙格楞次矢量的守恒性可以启发氢原子的另一守恒量:
检查其对易关系:
其对应了新的三个生成元:
这说明SO(4)
计算分量的对易关系:
我们记$\hat N=(\frac{m}{-2E})^\frac12\hat M$:
对三维坐标动量引入第四维坐标和动量,则会多三个角动量:
定义重组算符:
那么:
重组算符可以看作独立的角动量算符,那么:
他们分别具有本征值:$i(i+1)\hbar^2$和$k(k+1)\hbar^2$
由于
另外:
宇称对称性
宇称变换定义为:
可以推导出以下性质:
- 对动量本征态的变换:
- 对位移算符的变换:
- 对动量算符的变换:
- 对角动量算符的变换:
- 对平移算符的变换:
还有这些性质:
- 宇称算符的平方:
- 宇称算符的厄密性:
证明:
所以:
- 宇称算符的厄密性和逆算符又构成了幺正性:
- 宇称算符的幺正性要求其本征值为$e^{i\delta}$,又因为其厄密性,所以本征值只能是$\pm1$。
宇称算符的本征态
如果宇称算符和哈密顿算符对易:
并且$|n\rangle$是$\hat H$的非简并本征态,那么$|n\rangle$同时也是宇称算符的本征态。
证明:
所以
如果$\lambda=1$,那么是偶宇称;如果$\lambda=-1$,那么是奇宇称。
如果是简并的,那么在这一步会出现问题:
其中$m$是和$n$不同的本征态。
这个定义指出如果哈密顿算符对称,那么其本征态也具有对称性。
例如:
- 量子谐振子$|0\rangle$是偶宇称的,但是$|1\rangle=\hat a^\dagger|0\rangle$是奇的,因为作用在$\hat a^\dagger$会变号;
- 自由粒子由于是简并的,所以$\hat \Pi|\vec{p}\rangle=|\vec{-p}\rangle$;
- 角动量的本征态:由于$\hat \Pi Y_{l,m}=(-1)^lY_{l,m}$,也就是说奇偶宇称只跟l有关。
自发对称性破缺
宇称选择定则
我们似乎发现有些量被宇称操作的结果是不一样的,实际上有如下结果:
| Classification | Parity | Rotations |
|---|---|---|
| $\text{true vector }\hat{\mathbf{V}}$ | $\left\{\hat{\Pi},\hat{V}_i\right\}=0$ | $\left[\hat{L}_i,\hat{V}_j\right]=i \hbar \epsilon_{ijk} \hat{V}_k$ |
| $\text{pseudovector }\hat{\mathbf{V}}$ | $\left[\hat{\Pi},\hat{V}_i\right]=0$ | $\left[\hat{L}_i,\hat{V}_j\right]=i \hbar \epsilon_{ijk} \hat{V}_k$ |
| $\text{true scalar }\hat{f}$ | $\left[\hat{\Pi},\hat{f}\right]=0$ | $\left[\hat{L}_i,\hat{f}\right]=0$ |
| $\text{pseudoscalar }\hat{f}$ | $\left\{\hat{\Pi},\hat{f}\right\}=0$ | $\left[\hat{L}_i,\hat{f}\right]=0$ |
奇宇称算符,或者说实矢量或赝标量,其算符不能连接宇称相同的量子态,即如下定理:
如果$|\alpha\rangle$和$|\beta\rangle$是宇称算符的两个本征态,且他们的宇称相同,即
那么:
证明:
证毕。
时间反演对称性
经典力学的时间反演
量子力学的时间反演
考虑时间反演算符:
代入原来的薛定谔方程检验:
当然,以上需要$\hat H$是时间反演对称的。
时间反演算符
时间反演算符是一个反线性算符,即:
可以写成:
其中$\hat U$是幺正算符,$\hat K$是复共轭算符。
时间反演算符的性质
先考虑复共轭算符的性质:
- 复共轭算符会改变系数;
- 复共轭算符不会改变基矢本身。
一个严峻的问题是,对于不同的基矢选取,复共轭算符的作用是不同的。以$\hat S_y$为例,如果以$|\hat S_z,\pm\rangle$为基矢,那么复共轭算符会改变$|\hat S_y,\pm\rangle$:
另一方面,如果以$|\hat S_y,\pm\rangle$为基矢,那么复共轭算符并不会改变$|\hat S_y,\pm\rangle$。这意味着幺正算符$\hat U$是依赖于基矢的选取的。
内积
考虑时间反演后的内积:
算符
- 对于坐标算符:
- 对于动量算符:
- 对于角动量算符:
波函数
定理:如果无关自旋的哈密顿量在时间反演下不变,且本征右矢$|n\rangle$是非简并的,则相应的本征函数一定是实数的。
证明:
所以:
选取某一表象下的波函数:
所以:
证毕。
- 对于球谐函数:
- 对于平面波:
这两者并非实数,是因为他们是简并的。
有自旋波函数
对于自旋为1/2的粒子,我们可以定量写出时间反演算符的作用。
假设幺正算符是泡利矩阵中的一种:
限制条件:
即:
只有$\hat \sigma_y$满足条件:
所以自旋系统中的时间反演算符是:
一般写为:
自然就有:
克拉默定理:对一个自旋半整数的体系,如果其时间反演对称,那么其本征态一定简并。
证明:显然有
现在已经满足时间反演对称,即
如果是非简并的,那么:
那么:
这与前面的结论矛盾,所以一定是简并的。
反过来说,当外加磁场时,简并被破坏,也就说明了时间反演对称性被破坏。