单元系的相变
单元系的单相平衡条件(热动平衡判据)
热力学第二定律指出,孤立系统的熵朝着增加的方向进行,如果孤立系统处于稳定平衡态,其熵一定是极大值:
对于其他系统也是如此:
- 孤立系统:$\delta S=0, \delta^2 S<0$
- 等温等容系统:$\delta F=0, \delta^2 F>0$
- 等温等压系统:$\delta G=0, \delta^2 G>0$
作为以上的应用,可以推导出均匀系统的稳定平衡条件:
推导过程:
取均匀孤立系统的一小部分,由于系统是孤立的,那么有:
熵的变化为:
由熵判据,得:
由热力学基本方程,得:
代入熵判据可得:
虚变动是任意的,所以一阶熵判据给出:
二阶熵判据给出:
所以二阶熵判据等价为:
孤立系统的熵判据又称为热动平衡判据,因为温度相等即是热力学平衡,压强相等即是动力学平衡。
单元复相系的热力学基本方程
我们曾定义温度为两个系统能量交换平衡的判据,定义压强为两个系统体积交换平衡的判据,现在两个系统还可以交换粒子数(物质的量),我们则定义化学势为粒子数交换的平衡判据。然而化学势最初只是被定义为吉布斯函数随物质的量增加的系数,在后面两节会重新推导出平衡的定义。
以上两个系统整体看作孤立系统,所以不涉及外场。事实上,当系统为单元复相系的时候,这两个系统就是两个不同的相,为两个开系。
当我们把吉布斯函数写成温度和压强的函数$G(T,p)$的时候:
然而没有考虑物质的量发生变化的情况,我们予以考虑$G(T,p,n)$:
其中:
根据化学势的定义,吉布斯函数可以写为$G=nG_m=\mu n$,四个热力学基本方程被改写为:
定义巨热力势:
其全微分关系为:
显然:
巨热力势可以理解为在将系统“挤压”到体积为零的过程中所能获得的能量,是一个负值。
单元系的复相平衡条件
根据熵判据:
所以整个系统的熵变为:
这说明复相系的平衡条件为:
这包含了热动平衡和相变平衡,统称为复相平衡条件。
复相平衡的性质
相变平衡曲线
在不同的温度和压强下,系统可以处在不同的平衡态,双相平衡在相图中表现为两相平衡线,中间的区域即为单相平衡区。以下是最简单的水的$p-T$相图。
根据平衡理论,由于处在相变平衡曲线,相变曲线中相邻的两点满足化学势相等:
怎么求得化学势关于温度压强的微分关系呢?我们曾经在麦克斯韦关系中得到了方法:
其中
所以可以给出相变曲线的斜率方程,即克拉珀龙方程:
对于水来说,相变会吸收潜热:
所以原方程可以化简为:
当发生液相到气相的转变时,由于$V_m^\beta\gg V_m^\alpha$,有:
进一步认为潜热和温度无关,积分得:
超临界点和等温线
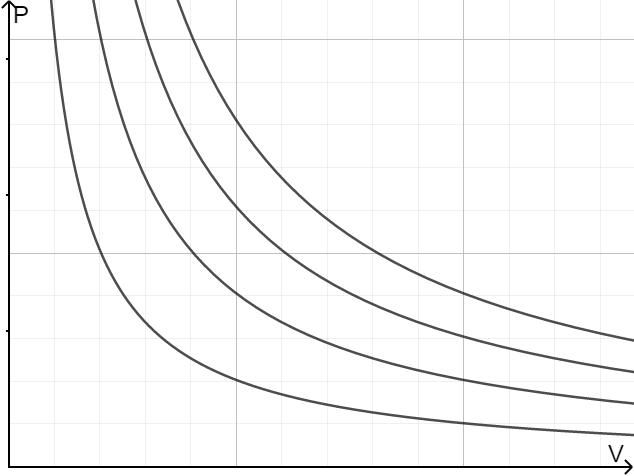
$p-T$相图的超临界点预示液相不再存在。对于二氧化碳来说,临界点为31.1°C。当温度超过临界温度,提高压强,二氧化碳不经过相变平衡曲线,所以其等温线接近理想气体的等温双曲线;如果温度小于临界点,由于会经过气液相变,其等温线存在如下“台阶”。

理想气体方程很容易描绘了等温线的形状:
范德瓦尔斯方程
给出了更接近现实的等温线:
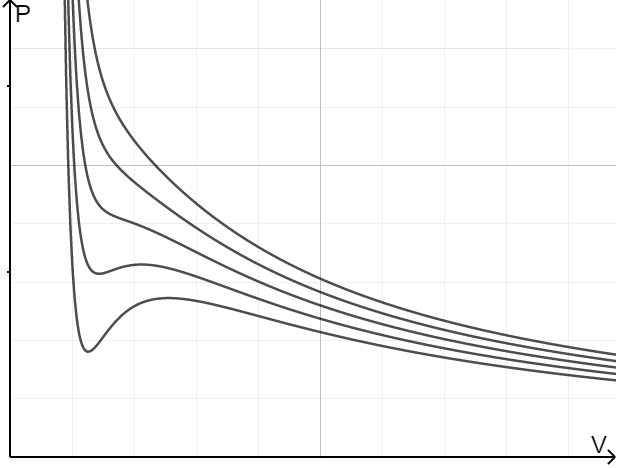
我们注意到,对于有的温度,等温线存在两个极值点;则有的等温线则不存在极值点。我们计算平滑变化的临界温度:
可以解得临界参数为:
当$T\leq T_c$的时候,该区域由于$(\dfrac{\partial^2 p}{\partial V_m^2})_T\leq0$,不稳定,气体会直接越过气液两相共存的阶段直接进入液相。
我们知道
这其实是等温线左侧的面积,我们观察到这个面积的图像应该如下:

只有KBAMR曲线是稳定的,我们就找到了真正的等温线。
相变的分类
一级相变:相变点两端的化学势连续,但是一阶偏导数不连续。一级相变有相变潜热(熵突变)和比体积突变。
这是因为$\mu=G_m=\frac{\partial G}{\partial n}$,所以
说白了就是水液化的时候会放热而且每摩尔体积缩小。
二级相变:相变点两端的化学势和一阶偏导数连续,但是二阶偏导数不连续。二级相变的定压比热、定压膨胀系数和等温压缩系数存在突变。
可以导出埃伦费斯特方程:
说白了就是化学势的多少阶微分突变,就是多少级相变。二级相变的例子有:超导金属,铁磁性物质的居里点,超流现象。
临界现象和朗道连续相变理论
一些物质在连续相变的时候,其热力学量在接近临界点时展现奇特的性质,且大部分表现出随序参量的幂律:
$\delta$被称为临界指数。
朗道提供了一种可能的解释:物质的状态与有序性(对称性)相关,所以物质相变的时候会发生对称性破缺;朗道定义了描述有序程度的序参量$\Gamma$,选择热力学势$F$和相应的参量,比如说$T$,那么由于在原点处平衡,有:
朗道相变理论指出,热力学势最低的地方自然是序参量的位置,而序参量的位置又和温度有关,所以可以构建序参量和温度的关系,这一关系是突变的,可以解释相变现象。
平衡态:
可以解出:
假设$\alpha(T)=\alpha_0\frac{T-T_c}{T_c}$,$\beta(T)=\beta_0$,则有:
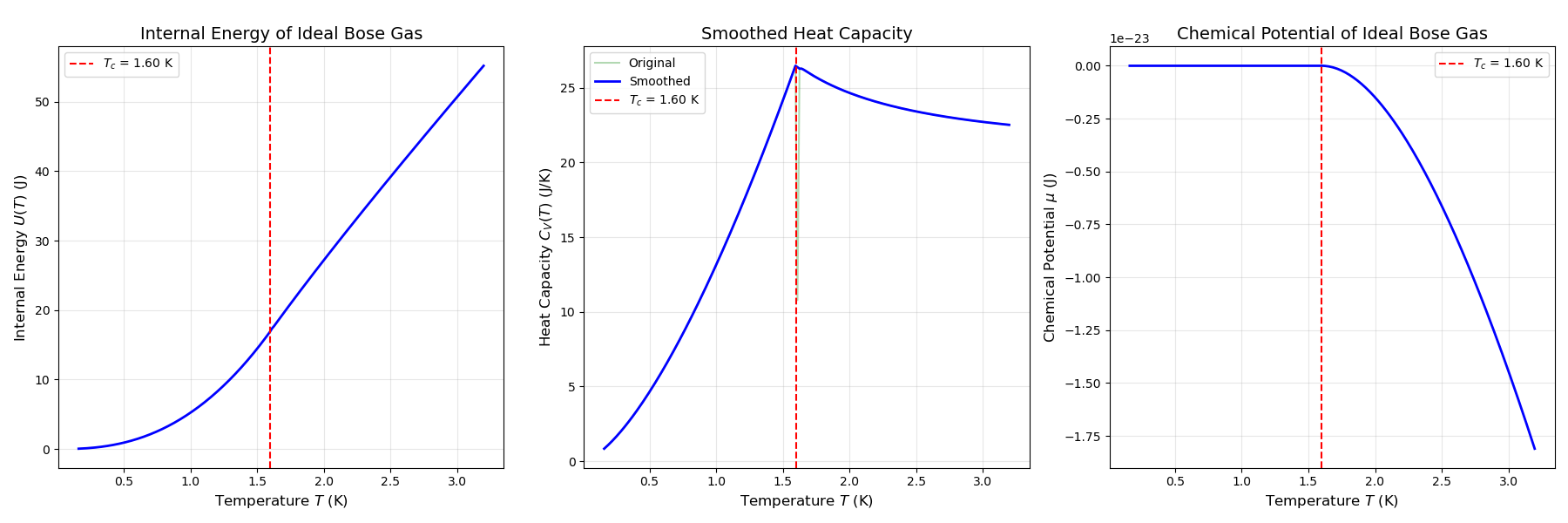
可以看到,比热在临界点处有突变,大小为$-\frac{\alpha^2}{2\beta T_c}$。