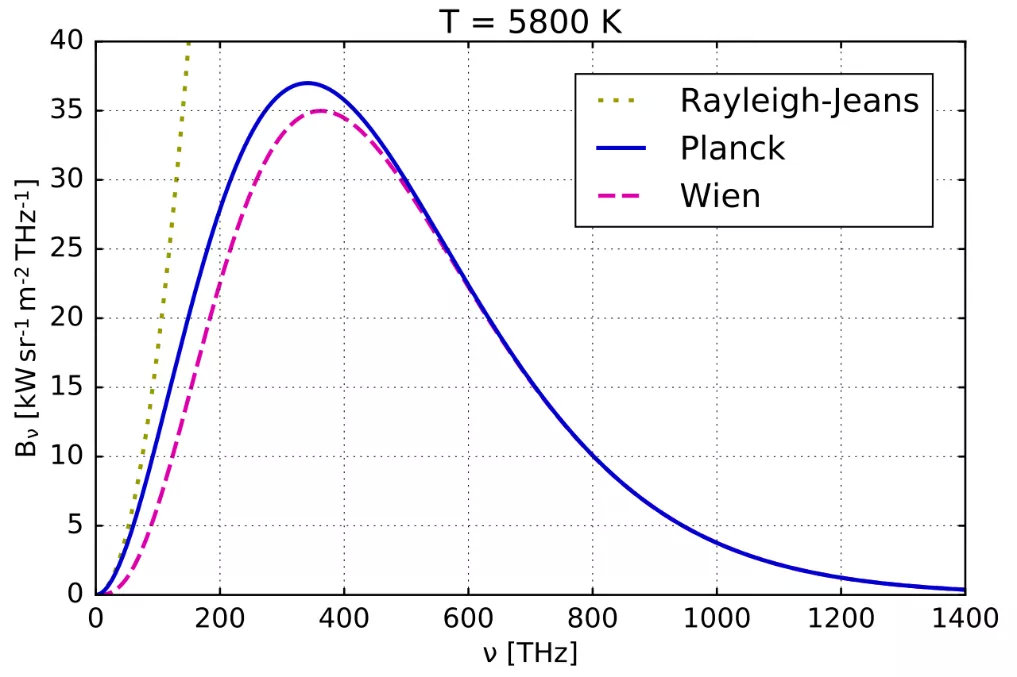
全同粒子
量子力学的基本假设规定基本粒子是不可区分的,不可区分的粒子即为全同粒子。当研究两个相同粒子体系的时候,不可避免涉及到相互作用的问题,为了简单起见,我们假设两个粒子没有相互作用。
波函数的交换对称性
既然两个粒子是不可区分的,他们的波函数满足:
这必然要求$\psi_{1,2}=e^{i\theta}\psi_{2,1}=e^{2i\theta}\psi_{1,2}$,也即:
这样似乎可以写出体系的波函数了:
这里似乎有几个小问题:
- 如果这两个态是相同的,也就是$\psi(x_1,x_2)=\psi_a(x_1)\psi_a(x_2)$,那么显然是交换对称的,不可能出现交换反对称的情况——这说明费米子不可能占据同一个态(泡利不相容原理)。
- 如果这两个态不相同,那为什么不写成$\psi(x_1,x_2)=\psi_b(x_1)\psi_a(x_2)$?这似乎违背了全同粒子的概念,于是只好写成: 这和泡利不相容原理是一致的,当两个态相同的时候,该式子退化为0。我们在Slater行列式中也能观察到这种情况。
交换力
对于以下三种情况,分别计算两个粒子间距离的方差:
- $\psi(x_1,x_2)=\psi_a(x_1)\psi_b(x_2)$
- $\psi(x_1,x_2)=\frac 1{\sqrt{2}}(\psi_a(x_1)\psi_b(x_2)\pm\psi_b(x_1)\psi_a(x_2))$
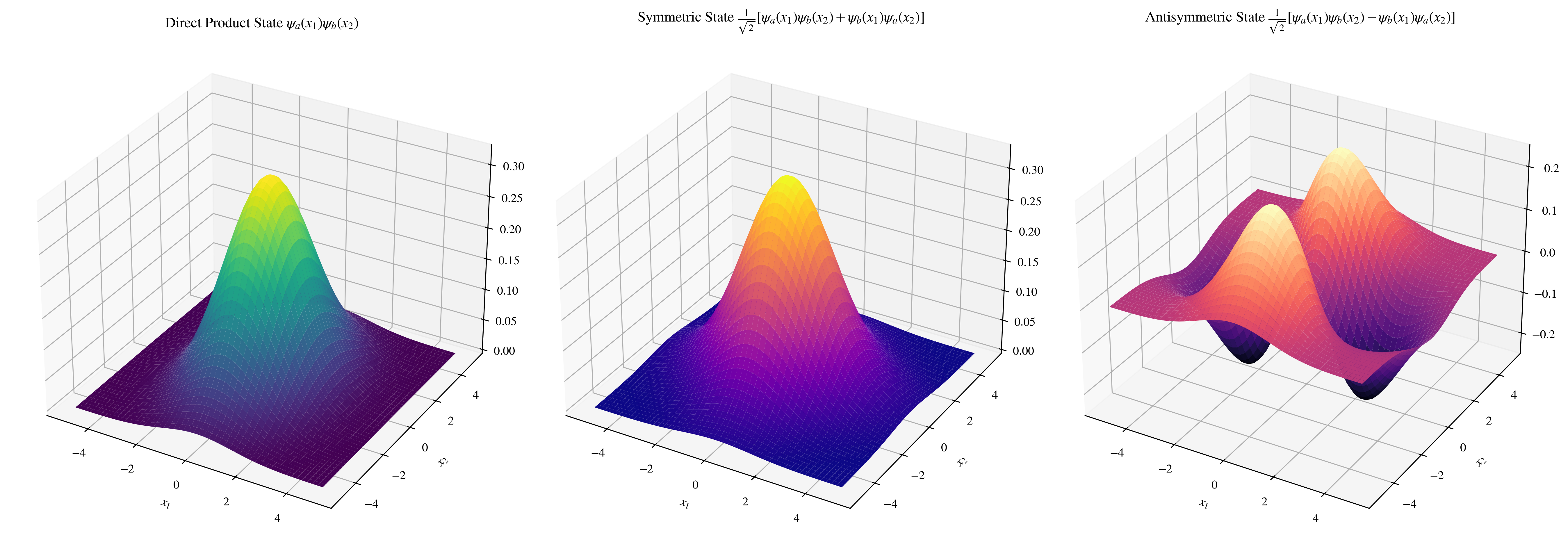
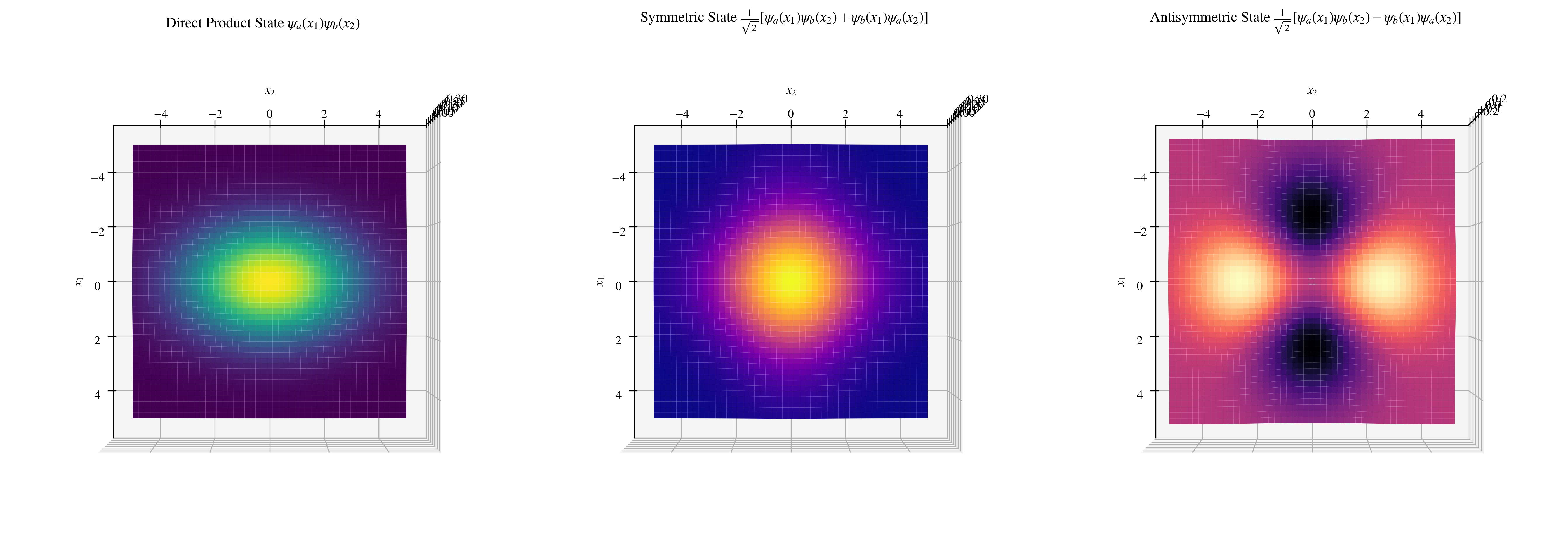
这样看似乎很抽象——为什么两个粒子之间的距离会凭空变化呢?下面做了一些演示,对于给定正态分布的$\psi_a$和$\psi_b$,当交换变量并叠加时,的确会因为交换(反)对称而变得聚集(分散)。
import numpy as np |
费米子,玻色子和泡利不相容原理
定义交换算符$\hat{P}$为:
显然,$\hat{P}^2=1$,意味着交换算符的本征值为$\pm 1$。可以证明,交换算符和哈密顿算符是对易的:$[\hat{P},\hat{H}]=0$,因此交换算符的本征态不变。对称化公理告诉我们,对于全同粒子,所有的状态只有两种可能的对称性:交换对称和交换反对称,而不存在其他对称性(或线性组合)。
将交换算符推广到多粒子体系,定义为:
经实验统计:
- 呈现交换对称的粒子自旋为整数,称为玻色子;
- 呈现交换反对称的粒子自旋为半整数,称为费米子。费米子还满足泡利不相容原理,即同一状态(由一组完备的量子数表述)只能容1个费米子。
对于占据$k_1<k_2<\ldots<k_N$态,坐标分别是$x_1,x_2,\ldots,x_N$的多粒子体系的波函数可以写成:
费米子的波函数由Slater行列式给出,这是好理解的,其中由于泡利不相容原理,只有$\frac{1}{\sqrt{N!}}$种可能。但是玻色子的描述比较复杂,由于没有泡利不相容原理的限制,玻色子可以占据任意态:
所以总共有$\dfrac{N!}{\prod_{i=1}^{N}n_i!}$种可能。遍历下标为$\{k_i\}$,其中$i=1,2,\ldots,N$是任意的。
将粒子进行编号然后遍历本身是复杂的,在二次量子化后采用粒子数表象可以大大简化。
元素周期表与洪特规则
在 中心力场问题 中,我们讨论了氢原子的对主量子数的简并是$n^2$,考虑电子有两个自旋,则第n个壳层可以容纳$2n^2$个电子。
如果电子是玻色子,那么由于玻色子可以占据同一态,因此每个电子都会跌落基态$(1,0,0)$。但是电子是费米子,因此每个电子都要占据不同的态。如果不考虑其他因素,那么元素周期表的列数依次为$2,8,18,32$。实际上,由于电子的屏蔽效应,元素周期表的列数依次为$2,8,8,18,18$。
利用洪特规则可以确定原子的基态:
- 第一规则:总自旋$S$越大,能量越低;
- 第二规则:给定自旋$S$的情况下,总轨道角动量$L$越大,能量越低。
- 第三规则:给定自旋$S$和轨道角动量$L$的情况下,如果未填满半壳层,总角动量$J$越小,能量越低;反之,总角动量$J$越大,能量越低。
第一规则是什么意思呢?直观地说,就是:在不违反泡利不相容原理的情况下,两个电子倾向于自旋平行($S=1$),而不是自旋反平行($S=0$);
- 在碳的$^3P_{0,1,2}$,$^1P_{1}$态中,第一规则选择了$^3P_{0,1,2}$态。(下面有举例)
- 在氦的激发态$^3S_1$,$^1S_0$中,第一规则认为$^3S_1$态能量更低。
我们以氦的激发态来验证这一点:氦原子的自旋波函数记为:
空间波函数为:
氦原子的哈密顿量为:
考虑费米子反对称性的要求,一共可以组合成4个本征态。不过我们不区分三重态的能量区别。只有$1/r_{12}$会导致结果的不同:
由于$1/r_{12}$是正定的,因此$\langle \psi_{tri}|\frac{1}{r_{12}}|\psi_{tri}\rangle<\langle \psi_{sing}|\frac{1}{r_{12}}|\psi_{sing}\rangle$,三重态能量小于单重态。这一点也可以从几何上理解,由上述交换力可知,单重态的空间对称的两个电子相聚更近,所以能量更高。
你可能会纳闷,这里似乎出现了两种方法来构造具有对称性的波函数,一种是通过slater行列式,另一种是通过CG系数。实际上,这两种方法是等价的,不过后者找出本征态是前者的线性组合。以下举出激发态氦原子$1s2s$和基态氦原子$(1s)^2$的例子:
对于非同科电子,把两个空间波函数和两个自旋波函数相组合,得到4个slater行列式:
其中,前两个波函数已经做到了空间和自旋的分离,现在我们来对后面两个做些变换。和上面一样,设对称和反对称的空间波函数$\psi_{space}^{sym}$和$\psi_{space}^{anti}$:
看到这你可能就恍然大“雾”了!把后两个稍微组合一下,这不正是 角动量耦合 中所找到的本征态的吗?而且还天然满足了对称性要求!这四个本征态刚好对应了上述我们求解激发态氦原子的四个本征态。所以上面我们的基本假设是正确的。
对于同科电子,$\psi_{1s}=\psi_{2s}$,则空间反对称波函数为零:$\psi_{space}^{anti}=0$,那么只剩下后两个波函数(组合后只剩一个,正好和$^1S_0$对的上)。可以看到,这正是由于泡利不相容原理,两个同科电子不能占据同一态。
以下是利用洪特规则从可能的电子组态中确定基态:
| 原子序数$Z$ | 元素 | 电子排布 | 电子组态 | 基态 | 备注 |
|---|---|---|---|---|---|
| 1 | $H$ | $(1s)$ | $^2S_{1/2}$ | $^2S_{1/2}$ | 后面将看到,这是半满层的一个特例 |
| 2 | $He$ | $(1s)^2$ | $^1S_0$,$^3S_1$ | $^1S_0$ | 泡利不相容原理排除$^3S_1$(满壳层) |
| 3 | $Li$ | $(He)(2s)$ | $^2S_{1/2}$ | $^2S_{1/2}$ | |
| 4 | $Be$ | $(He)(2s)^2$ | $^1S_0$,$^3S_1$ | $^1S_0$ | |
| 5 | $B$ | $(He)(2s)^2(2p)$ | $^2P_{1/2}$,$^2P_{3/2}$ | $^2P_{1/2}$ | $L=1;S=\frac12$,洪特第三规则选择$^2P_{1/2}$ |
| 6 | $C$ | $(He)(2s)^2(2p)^2$ | $^3P_{0,1,2}$,$^1S_{0}$,$^1D_{2}$ | $^3P_0$ | $L=0,1,2;S=0,1$,费米子只允许$^1S$,$^1D$,$^3P$,泡利不相容原理排除$^1D_2$(两个$m_l=1$的电子),洪特第一规则选择$^3P_{0,1,2}$,第三规则选择$^3P_{0}$ |
| 7 | $N$ | $(He)(2s)^2(2p)^3$ | $^4S_{3/2}\cdots$ | $^4S_{3/2}$ | $L=1,2,3;S=\frac12,\frac32$,洪特第一规则选择$S=\frac32$(此时自旋是对称的),由于半满层的特殊性,只有$L=0$才能构造完全对称的态($m_l=1,0,-1$) |
| 8 | $O$ | $(He)(2s)^2(2p)^4$ | $^3P_{0,1,2}$,$^1S_{0}$,$^1D_{2}$ | $^3P_2$ | 类似$C$,不过要排布两个空穴 |
| 9 | $F$ | $(He)(2s)^2(2p)^5$ | $^2P_{1/2}$,$^2P_{3/2}$ | $^2P_{3/2}$ | 类似$B$,不过要排布一个空穴 |
| 10 | $Ne$ | $(He)(2s)^2(2p)^6$ | $^1S_0$,$^3S_1$ | $^1S_0$ | 满壳层 |
自由电子气
基于三维无限深方势阱,费米用自由电子气模型描述了费米子系统的一些性质。在费米子系统中,同一个能级只能容纳两个费米子。如果该系统一共有N个电子(N极大),那么最高能量可以计算如下:
其中$\rho=\frac{N}{L^3}$,该边界能量称为费米能。
总的能量可以积分为:
我们更关注和体积的关系,于是可以化简为:
这里可以解释0K金属的体积问题。当体积缩小的时候,金属向外的压力称为简并压,计算为:
这里补充二维自由电子气的结果:
这种简并压完全是一种量子效应,来源于全通费米子波函数的反对称要求。