全同粒子
量子力学的基本假设规定基本粒子是不可区分的，不可区分的粒子即为全同粒子。当研究两个相同粒子体系的时候，不可避免涉及到相互作用的问题，为了简单起见，我们假设两个粒子没有相互作用。
波函数的交换对称性
既然两个粒子是不可区分的，他们的波函数满足：
这必然要求$\psi_{1,2}=e^{i\theta}\psi_{2,1}=e^{2i\theta}\psi_{1,2}$，也即：
这样似乎可以写出体系的波函数了：
这里似乎有几个小问题：
- 如果这两个态是相同的，也就是$\psi(x_1,x_2)=\psi_a(x_1)\psi_a(x_2)$，那么显然是交换对称的，不可能出现交换反对称的情况——这似乎是泡利不相容原理的反命题。
- 如果这两个态不相同，那为什么不写成$\psi(x_1,x_2)=\psi_b(x_1)\psi_a(x_2)$？这似乎违背了全同粒子的概念，于是只好写成：
交换力
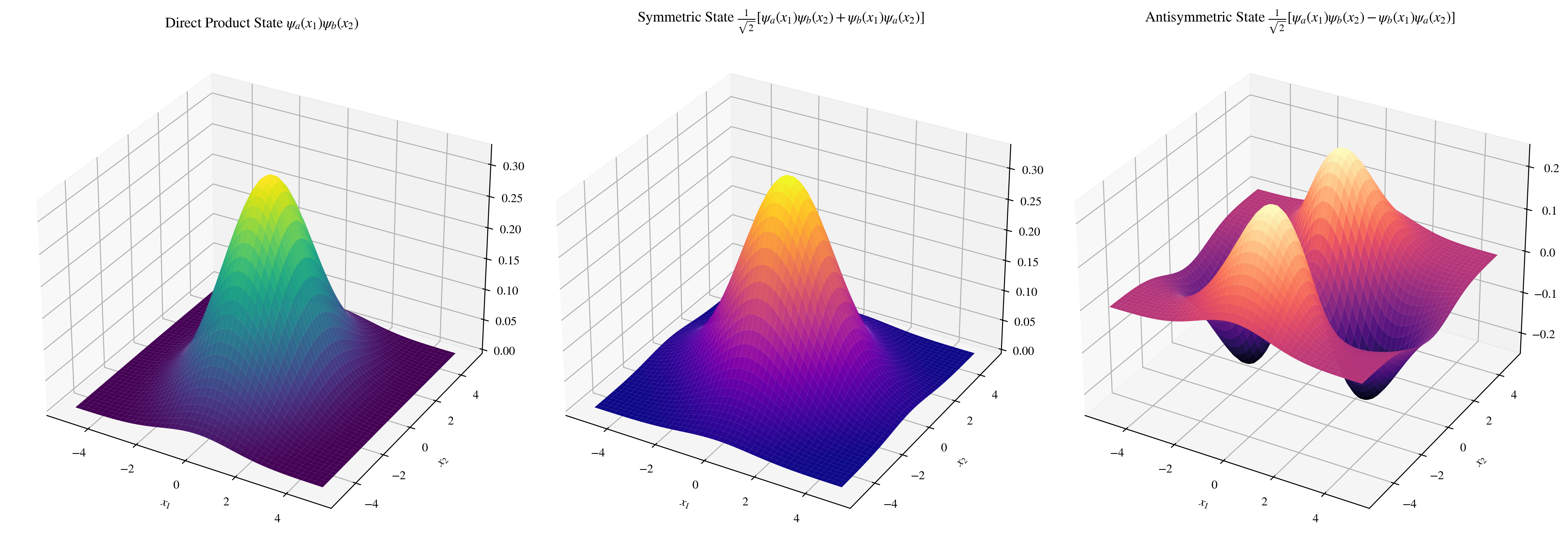
对于以下三种情况，分别计算两个粒子间距离的方差：
- $\psi(x_1,x_2)=\psi_a(x_1)\psi_b(x_2)$
- $\psi(x_1,x_2)=\frac 1{\sqrt{2}}(\psi_a(x_1)\psi_b(x_2)\pm\psi_b(x_1)\psi_a(x_2))$
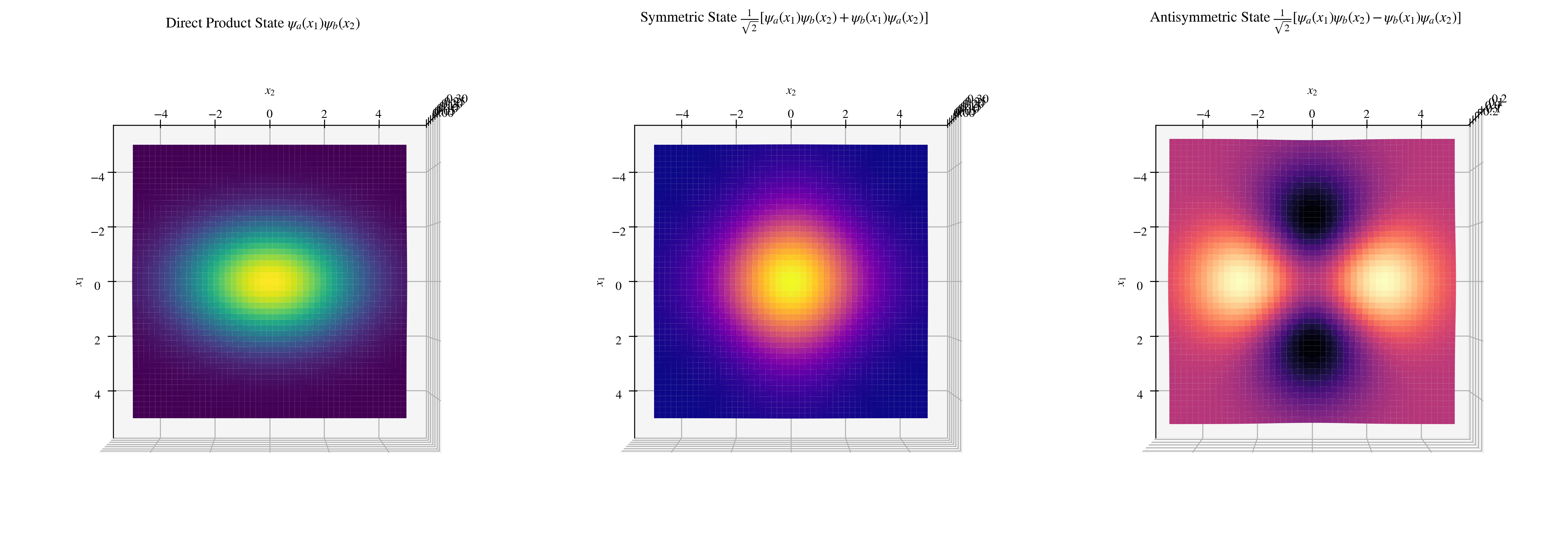
这样看似乎很抽象——为什么两个粒子之间的距离会凭空变化呢？下面做了一些演示，对于给定正态分布的$\psi_a$和$\psi_b$，当交换变量并叠加时，的确会因为交换（反）对称而变得聚集（分散）。
import numpy as np |
费米子，玻色子和泡利不相容原理
定义交换算符$\hat{P}$为：
显然，$\hat{P}^2=1$，意味着交换算符的本征值为$\pm 1$。可以证明，交换算符和哈密顿算符是对易的：$[\hat{P},\hat{H}]=0$，因此交换算符的本征态不变。对称化公理告诉我们，对于全同粒子，所有的状态只有两种可能的对称性：交换对称和交换反对称，而不存在其他对称性（或线性组合）。
将交换算符推广到多粒子体系，定义为：
经实验统计：
- 呈现交换对称的粒子自旋为整数，称为玻色子；
- 呈现交换反对称的粒子自旋为半整数，称为费米子。费米子还满足泡利不相容原理，即同一状态（由一组完备的量子数表述）只能容纳两个费米子。
对于占据$k_1<k_2<\ldots<k_N$态，坐标分别是$x_1,x_2,\ldots,x_N$的多粒子体系的波函数可以写成：
费米子的波函数由Slater行列式给出，这是好理解的，其中由于泡利不相容原理，只有$\frac{1}{\sqrt{N!}}$种可能。但是玻色子的描述比较复杂，由于没有泡利不相容原理的限制，玻色子可以占据任意态：
所以总共有$\dfrac{N!}{\prod_{i=1}^{N}n_i!}$种可能。遍历下标为$\{k_i\}$，其中$i=1,2,\ldots,N$是任意的。
将粒子进行编号然后遍历本身是复杂的，在二次量子化后采用粒子数表象可以大大简化。
元素周期表
在 中心力场问题 中，我们讨论了氢原子的对主量子数的简并是$n^2$，考虑电子有两个自旋，则第n个壳层可以容纳$2n^2$个电子。
如果电子是玻色子，那么由于玻色子可以占据同一态，因此每个电子都会跌落基态$(1,0,0)$。但是电子是费米子，因此每个电子都要占据不同的态。如果不考虑其他因素，那么元素周期表的列数依次为$2,8,18,32$。实际上，由于电子的屏蔽效应，元素周期表的列数依次为$2,8,8,18,18$。
利用洪特规则可以确定原子的基态：
- 第一规则：总自旋$S$越大，能量越低；
- 第二规则：给定自旋$S$的情况下，总轨道角动量$L$越大，能量越低。
- 第三规则：给定自旋$S$和轨道角动量$L$的情况下，如果未填满半壳层，总角动量$J$越小，能量越低；反之，总角动量$J$越大，能量越低。
第一规则是什么意思呢？直观地说，就是：在不违反泡利不相容原理的情况下，两个电子倾向于自旋平行（$S=1$），而不是自旋反平行（$S=0$）；
- 在碳的$^3P_{0,1,2}$,$^1P_{1}$态中，第一规则选择了$^3P_{0,1,2}$态。（下面有举例）
- 在氦的激发态$^3S_1$,$^1S_0$中，第一规则认为$^3S_1$态能量更低。
我们以氦的激发态来验证这一点：氦原子的自旋波函数记为：
空间波函数为：
氦原子的哈密顿量为：
考虑费米子反对称性的要求，一共可以组合成4个本征态。不过我们不区分三重态的能量区别。只有$1/r_{12}$会导致结果的不同：
由于$1/r_{12}$是正定的，因此$\langle \psi_{tri}|\frac{1}{r_{12}}|\psi_{tri}\rangle<\langle \psi_{sing}|\frac{1}{r_{12}}|\psi_{sing}\rangle$，三重态能量小于单重态。这一点也可以从几何上理解，由上述交换力可知，单重态的空间对称的两个电子相聚更近，所以能量更高。
你可能会纳闷，这里似乎出现了两种方法来构造具有对称性的波函数，一种是通过slater行列式，另一种是通过CG系数。实际上，这两种方法是等价的，不过后者找出本征态是前者的线性组合。以下举出激发态氦原子$1s2s$和基态氦原子$(1s)^2$的例子：
对于非同科电子，把两个空间波函数和两个自旋波函数相组合，得到4个slater行列式：
其中，前两个波函数已经做到了空间和自旋的分离，现在我们来对后面两个做些变换。和上面一样，设对称和反对称的空间波函数$\psi_{space}^{sym}$和$\psi_{space}^{anti}$：
看到这你可能就恍然大“雾”了！把后两个稍微组合一下，这不正是 角动量耦合 中所找到的本征态的吗？而且还天然满足了对称性要求！这四个本征态刚好对应了上述我们求解激发态氦原子的四个本征态。所以上面我们的基本假设是正确的。
对于同科电子，$\psi_{1s}=\psi_{2s}$，则空间反对称波函数为零：$\psi_{space}^{anti}=0$，那么只剩下后两个波函数（组合后只剩一个，正好和$^1S_0$对的上）。可以看到，这正是由于泡利不相容原理，两个同科电子不能占据同一态。
以下是利用洪特规则从可能的电子组态中确定基态：
| 原子序数$Z$ | 元素 | 电子排布 | 电子组态 | 基态 | 备注 |
|---|---|---|---|---|---|
| 1 | $H$ | $(1s)$ | $^2S_{1/2}$ | $^2S_{1/2}$ | 后面将看到，这是半满层的一个特例 |
| 2 | $He$ | $(1s)^2$ | $^1S_0$,$^3S_1$ | $^1S_0$ | 泡利不相容原理排除$^3S_1$（满壳层） |
| 3 | $Li$ | $(He)(2s)$ | $^2S_{1/2}$ | $^2S_{1/2}$ | |
| 4 | $Be$ | $(He)(2s)^2$ | $^1S_0$,$^3S_1$ | $^1S_0$ | |
| 5 | $B$ | $(He)(2s)^2(2p)$ | $^2P_{1/2}$,$^2P_{3/2}$ | $^2P_{1/2}$ | $L=1;S=\frac12$，洪特第三规则选择$^2P_{1/2}$ |
| 6 | $C$ | $(He)(2s)^2(2p)^2$ | $^3P_{0,1,2}$,$^1S_{0}$,$^1D_{2}$ | $^3P_0$ | $L=0,1,2;S=0,1$，费米子只允许$^1S$,$^1D$,$^3P$，泡利不相容原理排除$^1D_2$（两个$m_l=1$的电子），洪特第一规则选择$^3P_{0,1,2}$，第三规则选择$^3P_{0}$ |
| 7 | $N$ | $(He)(2s)^2(2p)^3$ | $^4S_{3/2}\cdots$ | $^4S_{3/2}$ | $L=1,2,3;S=\frac12,\frac32$，洪特第一规则选择$S=\frac32$（此时自旋是对称的），由于半满层的特殊性，只有$L=0$才能构造完全对称的态（$m_l=1,0,-1$） |
| 8 | $O$ | $(He)(2s)^2(2p)^4$ | $^3P_{0,1,2}$,$^1S_{0}$,$^1D_{2}$ | $^3P_2$ | 类似$C$，不过要排布两个空穴 |
| 9 | $F$ | $(He)(2s)^2(2p)^5$ | $^2P_{1/2}$,$^2P_{3/2}$ | $^2P_{3/2}$ | 类似$B$，不过要排布一个空穴 |
| 10 | $Ne$ | $(He)(2s)^2(2p)^6$ | $^1S_0$,$^3S_1$ | $^1S_0$ | 满壳层 |
自由电子气
基于三维无限深方势阱，费米用自由电子气模型描述了费米子系统的一些性质。在费米子系统中，同一个能级只能容纳两个费米子。如果该系统一共有N个电子（N极大），那么最高能量可以计算如下：
其中$\rho=\frac{N}{L^3}$，该边界能量称为费米能。
总的能量可以积分为：
我们更关注和体积的关系，于是可以化简为：
这里可以解释0K金属的体积问题。当体积缩小的时候，金属向外的压力称为简并压，计算为：
这里补充二维自由电子气的结果：
这种简并压完全是一种量子效应，来源于全通费米子波函数的反对称要求。
