计算物理5
问题
数值求解一维定态薛定谔方程 $(\hbar=1,m=1)$
取$m=1, V(x)=0.5x2+0.1x^6$, 在$-4<x<4$的范围内,画出基态波函数
和第一激发态波函数随空间的分布,同时求出基态和第一激发态的本征能量。
打靶法
打靶法的思路在于,如果波函数是无穷处收敛的,那么从较远的某端(值为0)开始以随机能量演化,到另一端的值如果也是0,那么认为该能量就是本征能量。
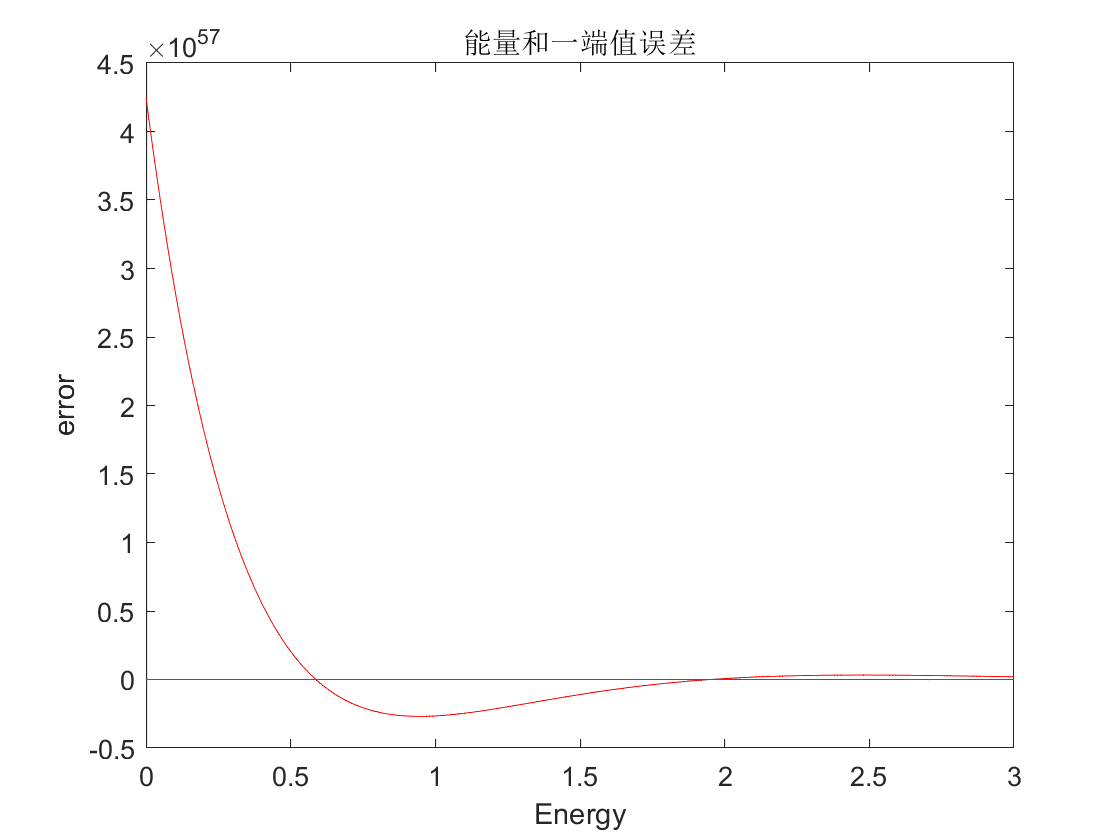
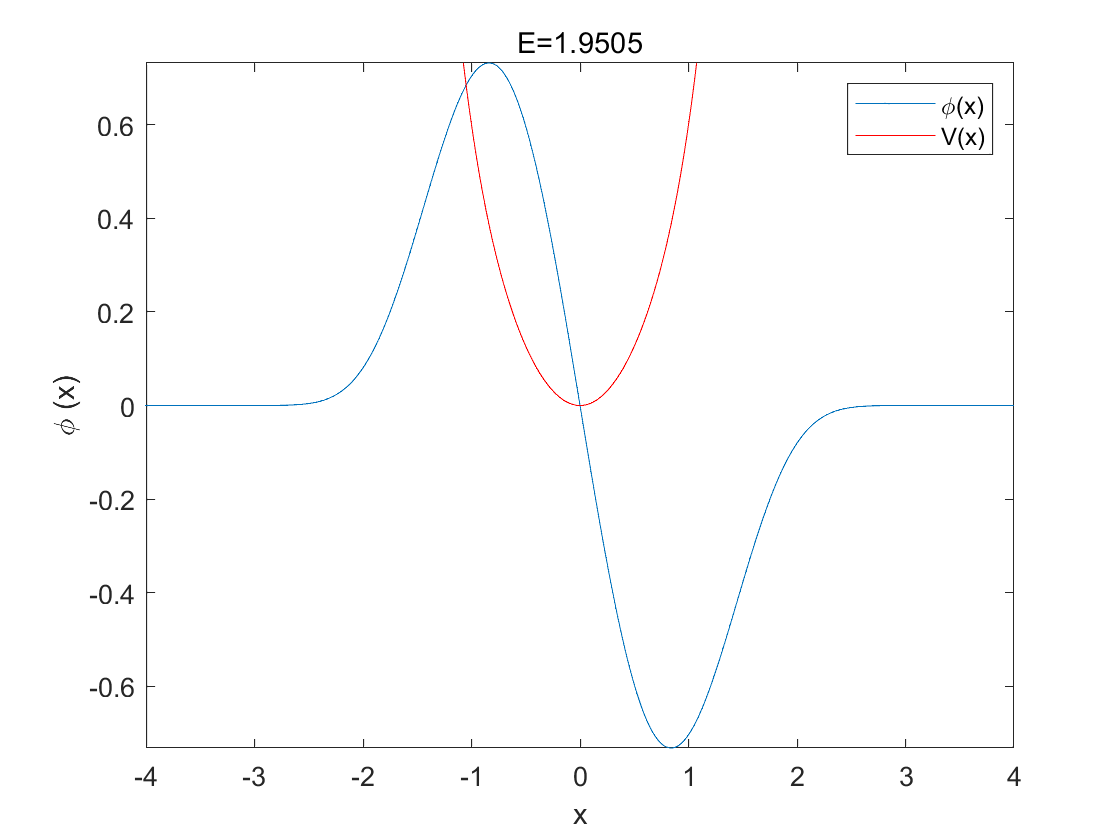
可以看到,基态的能量大概在[0.5,0.6],第一激发态大概在[1.9,2.0]。考虑到时间和精度的问题,再加上这里局部是单调的,那么采用二分法,计算得到:
画出波函数如图: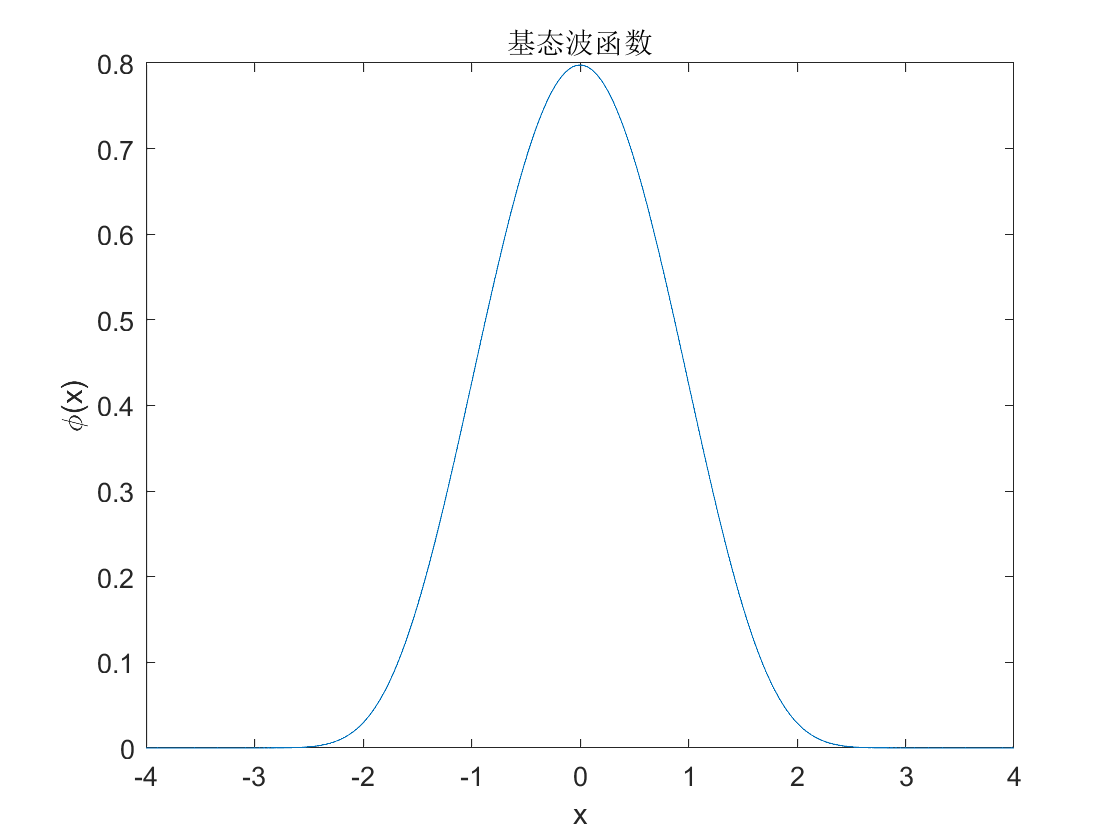
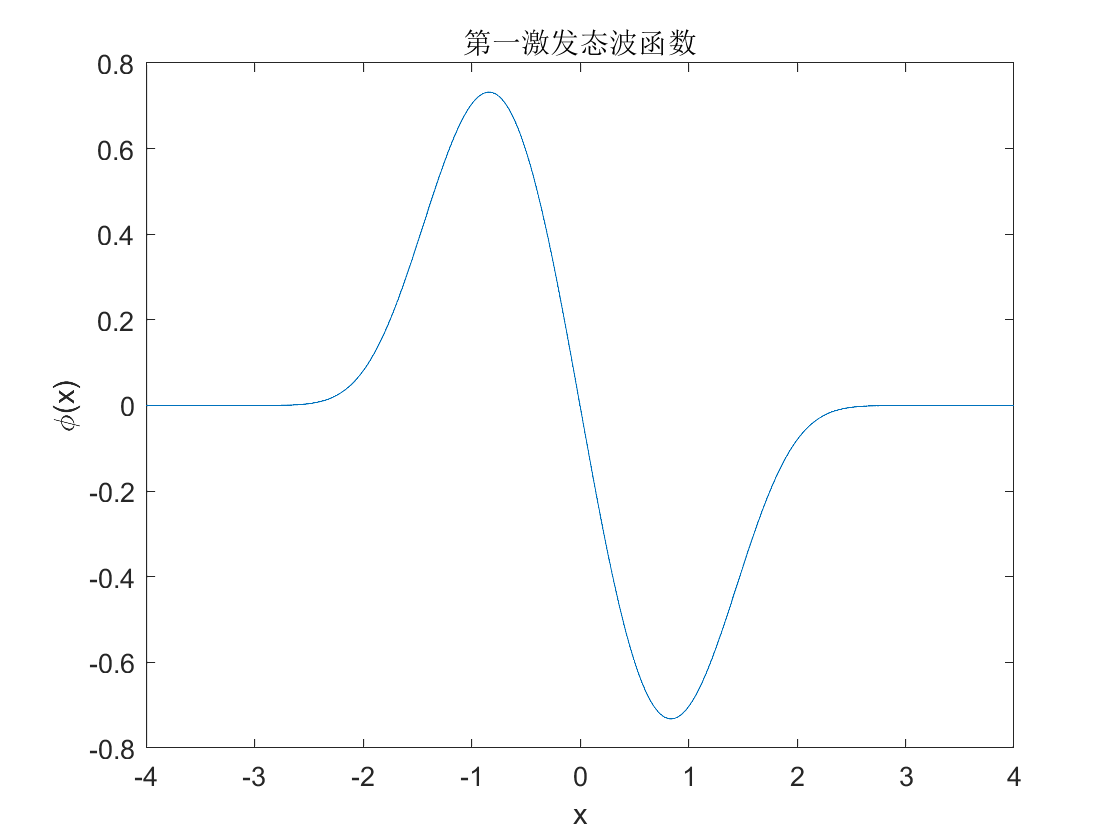
矩阵离散化求特征向量
其中$v=V(\Delta x)^2$。
这里用一阶近似展开了二阶导,所以误差如果要做的小,那么矩阵维度就要很大,计算量指数级上升。有兴趣的同学可以尝试高阶近似展开二阶导。
对上述矩阵提取特征值,可得
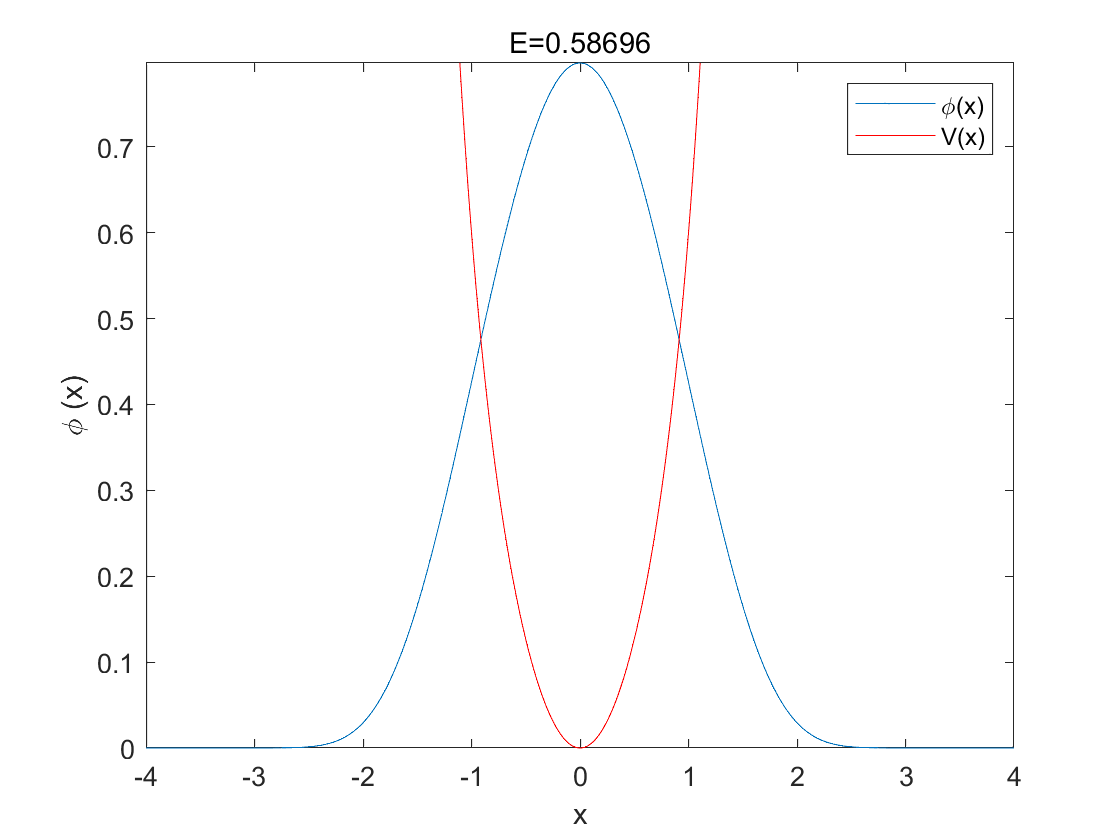
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 小径!



