计算物理4
问题
用四阶龙格库塔方法求解周期驱动单摆方程:
通过调节方程中的参数,以及初始条件,找到 $\phi=\pi$附近的稳定振动(建议通过相图的方式展示)。
用四阶龙格库塔方法求解一组耦合转的运动方程组:
其中$N=1000$是转子的个数,$\omega_i\in (-1,1)是均匀分布的转子的初速度$,$K$代表了耦合大小。从$\theta_i(t=0)=0$出发,定义
以及从物理上解释为什么会有这种差别分别计算K=0.2 和K=5时,r(t)的模 |r(t)| 随时间的演化,说明这两种情况下有何区别。
问题1
周期驱动单摆不同于普通单摆,可以稳定于 $\phi=\pi$,也可能出现在两个稳定点的跳跃,那么对稳定情况的约束需要考虑长时间稳定行为。定义步长$h=\frac{1}{10v}$,稳定条件为$|\mod{(\phi_{ave},2\pi)}-\pi|<0.02$,其中$\phi_{ave}$取最后500个点的平均。
在初值$\phi_0=\pi-0.001$情况下,画出$a-v$相图如下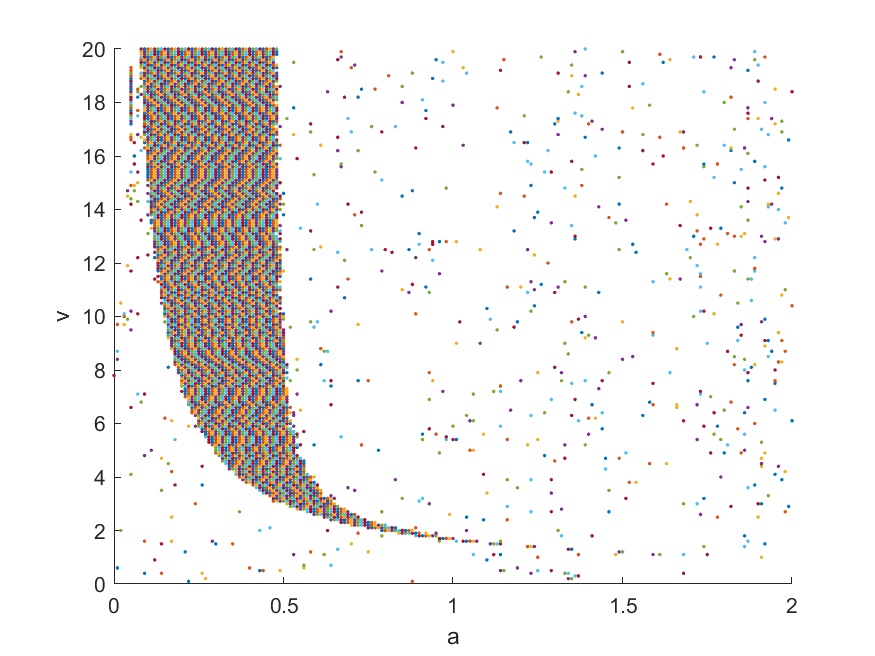
有兴趣的同学可以拟合这两条边界并进行解释,还可以分析初始条件的变化对相图的影响。
问题2
是转子系统的耦合程度——当所有转子指向相同的时候,该值取1,如果全部均匀随机取向,该值取0。
当耦合常数$K=0.2,5$时,得到的r值随时间的演化如图:
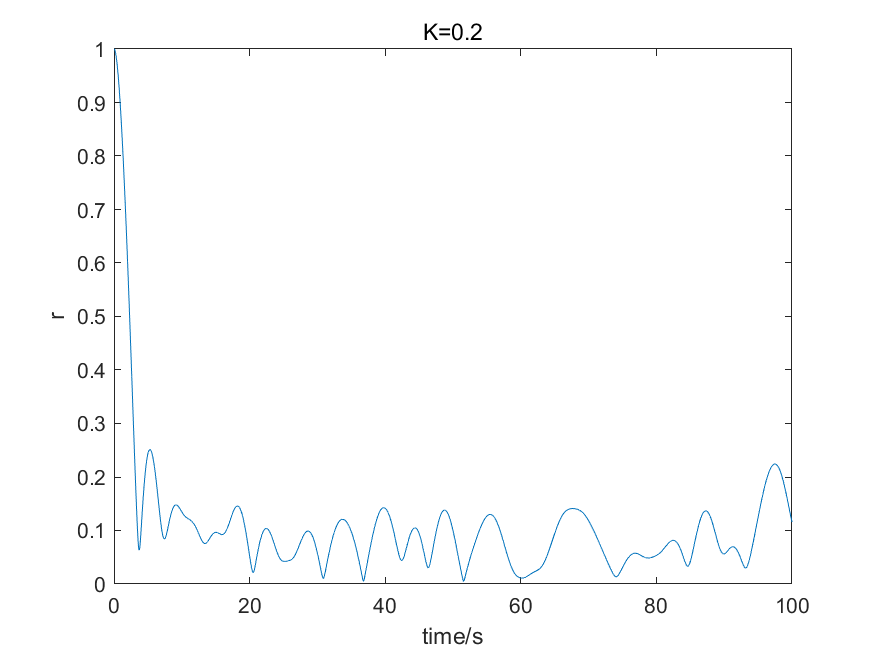
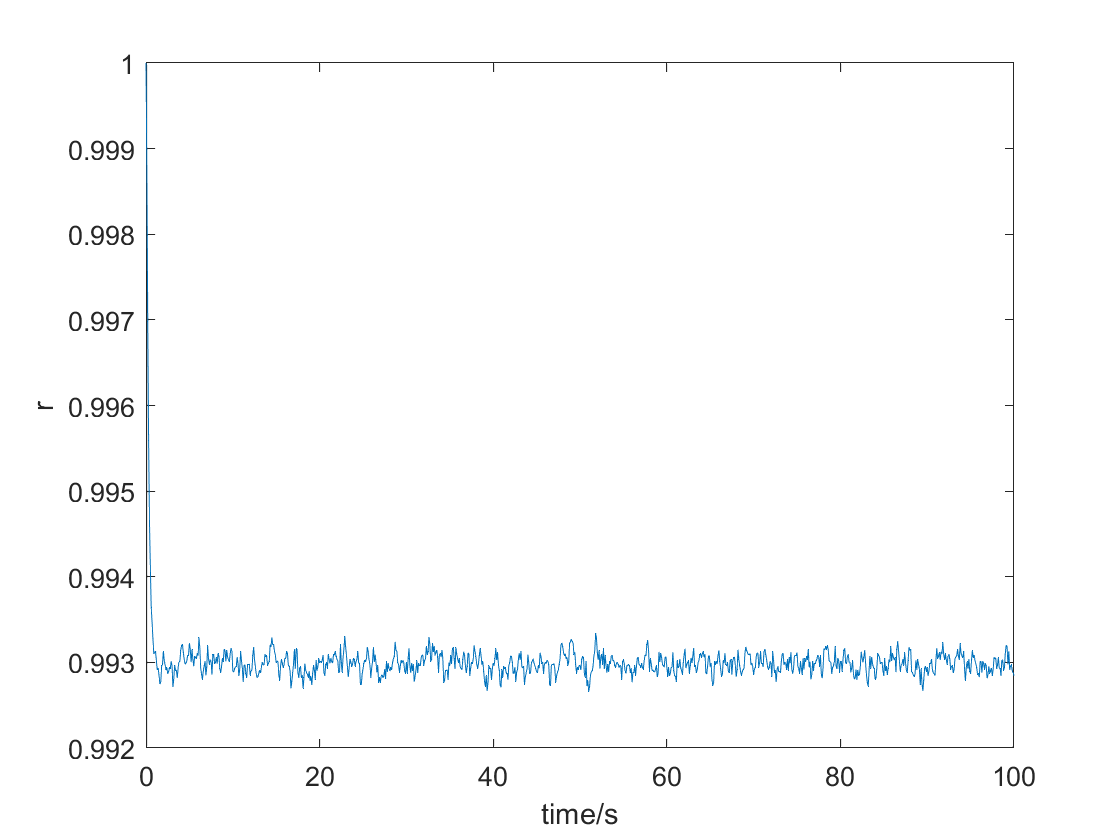
每个转子的角度变化如下
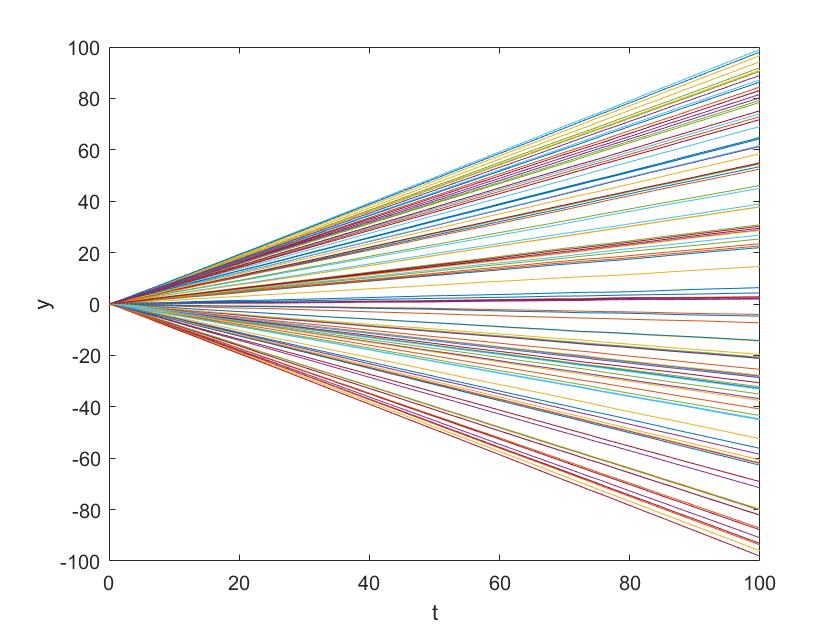
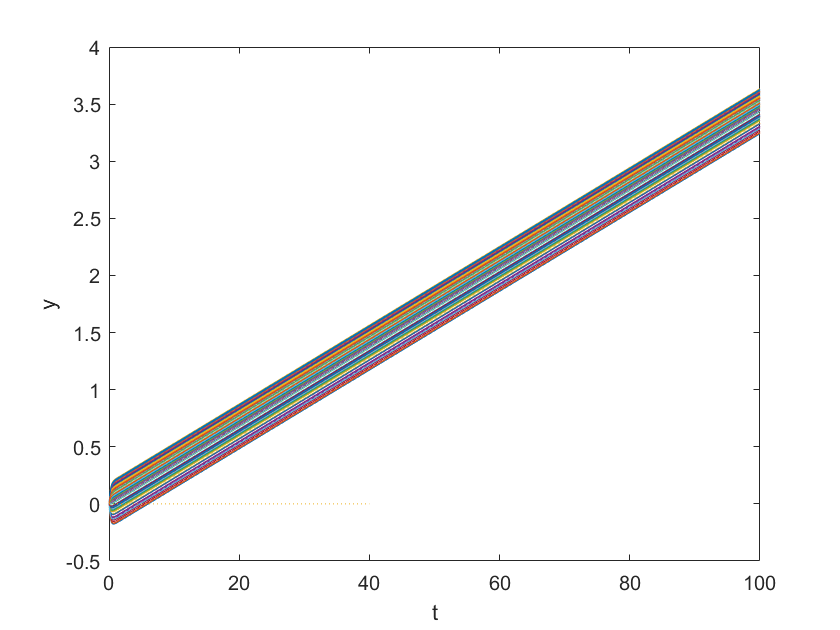
这是因为耦合常数小的时候,转子之间的关联并不大,初始取向随机,后续取向几乎不变,所以趋于0,同时回复力较小,r值变化比较平缓;耦合常数大的时候,所有转子的取向趋于相同,同时由于回复力较大,r值振动频繁。
画出K-r关系如下以验证: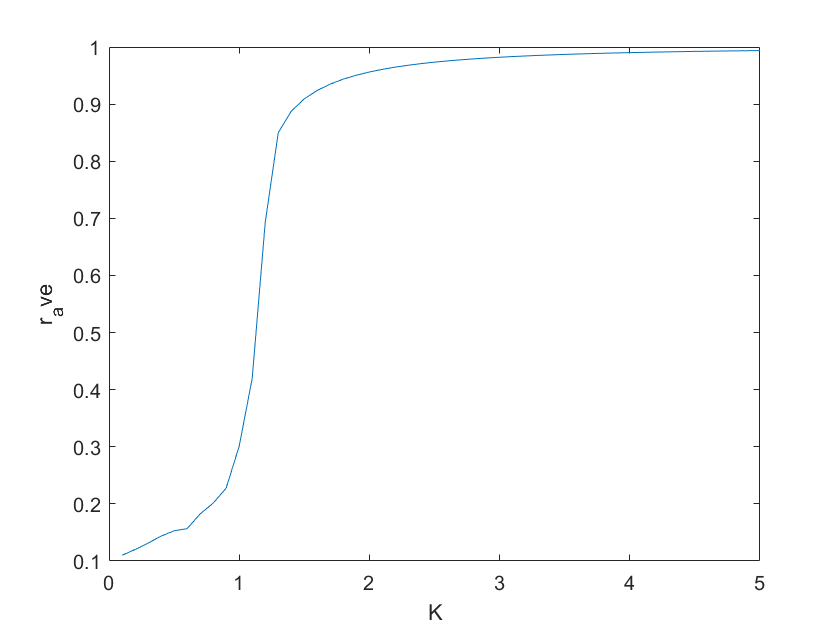
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 小径!



