开心消消乐

在一个$L\times L$的网格 (即每行每列均有$L$个格子)上定义如下的消消乐游戏：

  1. 在最开始，格子上没有任何的方块。

  2. 每次挑选任意一个格子，放上去一个方块。每放上去一个方块，系统开始演化一个时间
    步。一个时间步内的演化规则见后面一条。

  3. 如果一个格子上的方块数目大于等于4，则消去4个方块，并记录下这一次消去，这四个
    方块会移动累加到上下左右的4个格点(它们各自方块数+1),如果有一个方块的两个邻居同时消去并给到它，则它的方块数量+2,也就是说影响是叠加的；考虑开放边界条件，即如果一个格子在边界发生消去，则有一个或者两个方块移动出去了。每次同时消去所有当前高度大于等于4的格子，并记录下总的消去数。直到场上没有任何格子的方块数$\geq4$,这一个时间步结束。

  4. 每一步的得分记为这一步的总消去次数。

题目

  • 选取网格大小$L=32$,演化足够多的时间步，并记录网格平均方块数量($n=\frac{N}{L^2}$,$N$是场上的方块总数)随着演化时间$t$的关系。你发现了什么？
  • 选取并固定一个合适的系统尺寸$L$,统计长时间演化时，每步得分的频率分布。你发现了什么规律？
  • 选取多个不同的系统尺寸$L$重复 问题2 的过程，验证你发现的统计规律。系统的尺寸对这一规律有什么影响？
  • 你能解释你在 问题2 中发现的规律吗？

问题1：方块平均数量

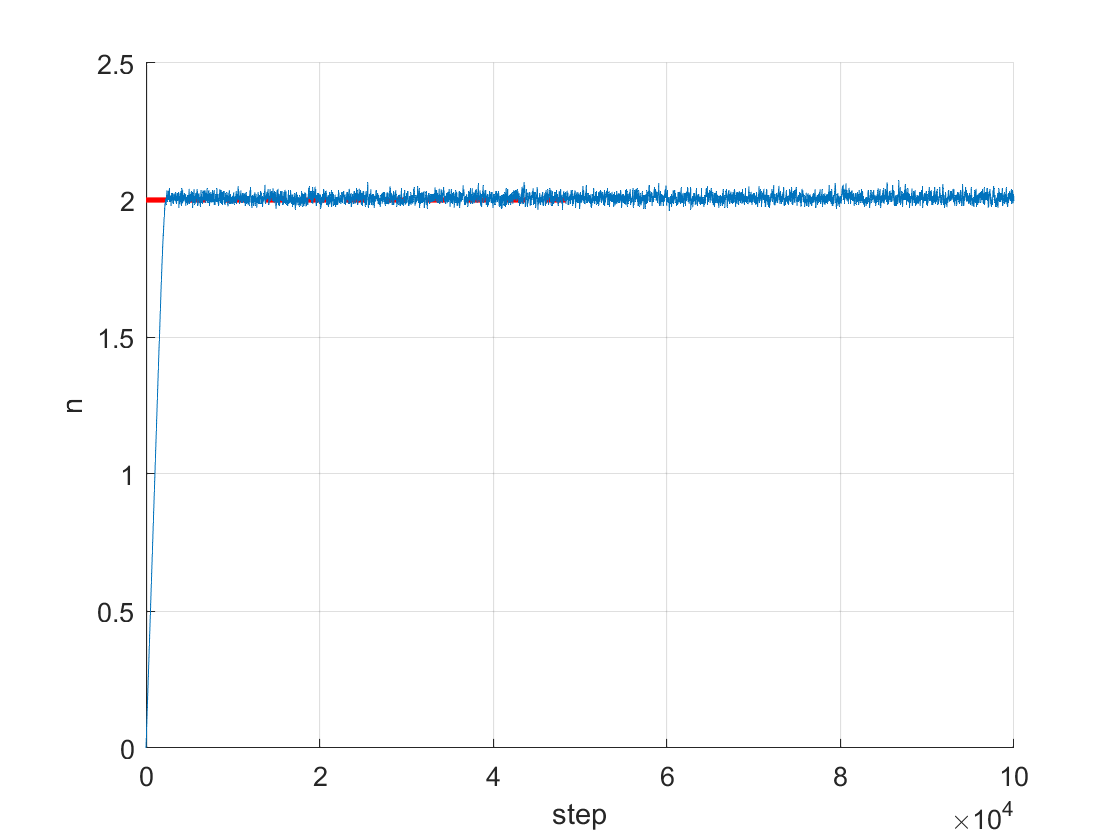
image

规律：

  • 平均方块较小时，平均方块数线性增加，增加速度约为$1/L^2$(当然因为方块移出边界的提前发生，会略小)；验证拟合结果
  • 平均方块数量稳定于一常数（与L有关）附近，取平均为$2.0078$。

注意：对更多的尺寸模拟可以知道，该常数不是2，随着L的增大而增大，个人猜测是发散的（一维的消消乐可以证实）。

问题2：得分频率分布

取平均方块数量稳定后的阶段进行得分频率统计：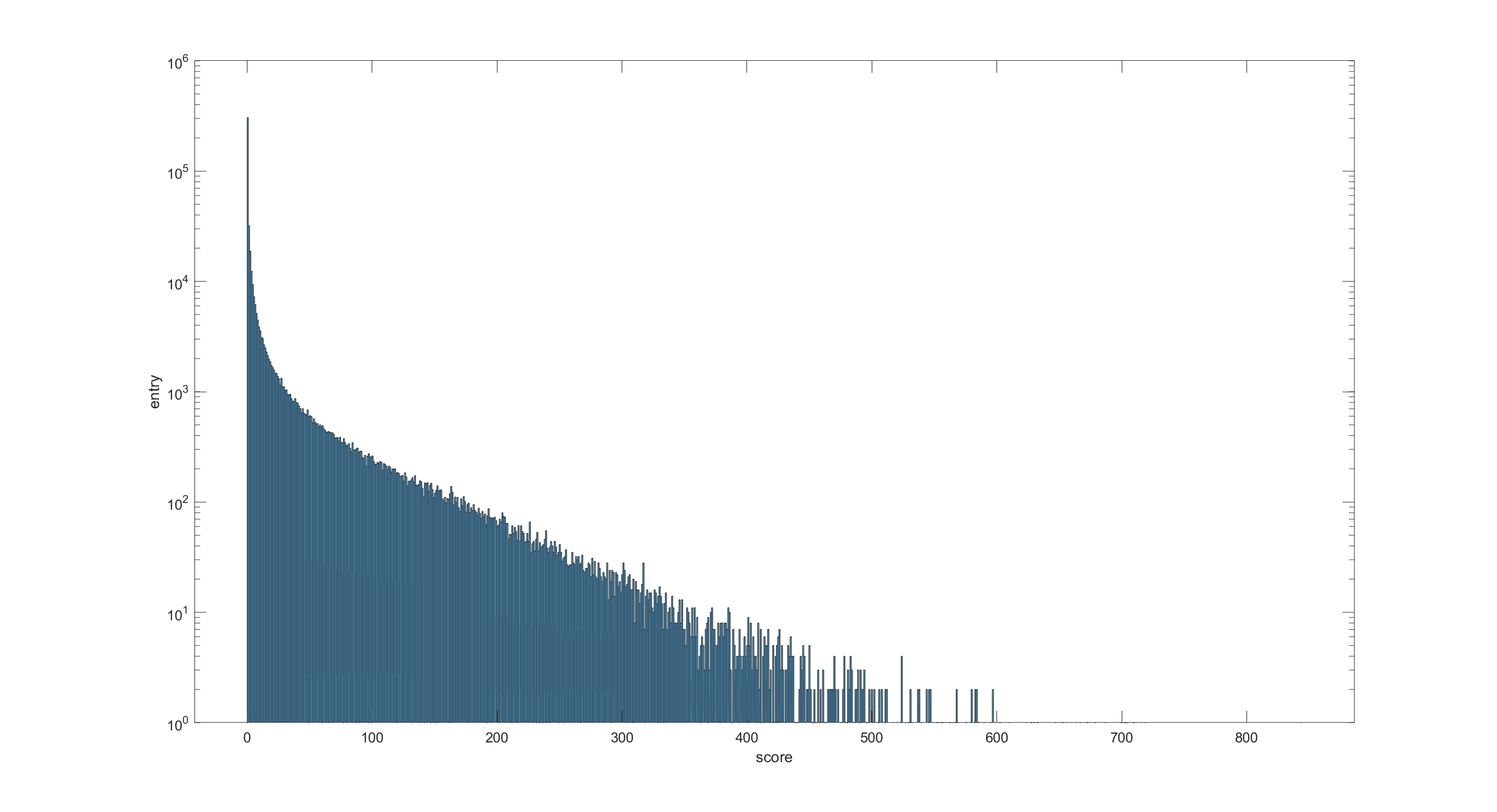
image
在双对数坐标图下进行展示：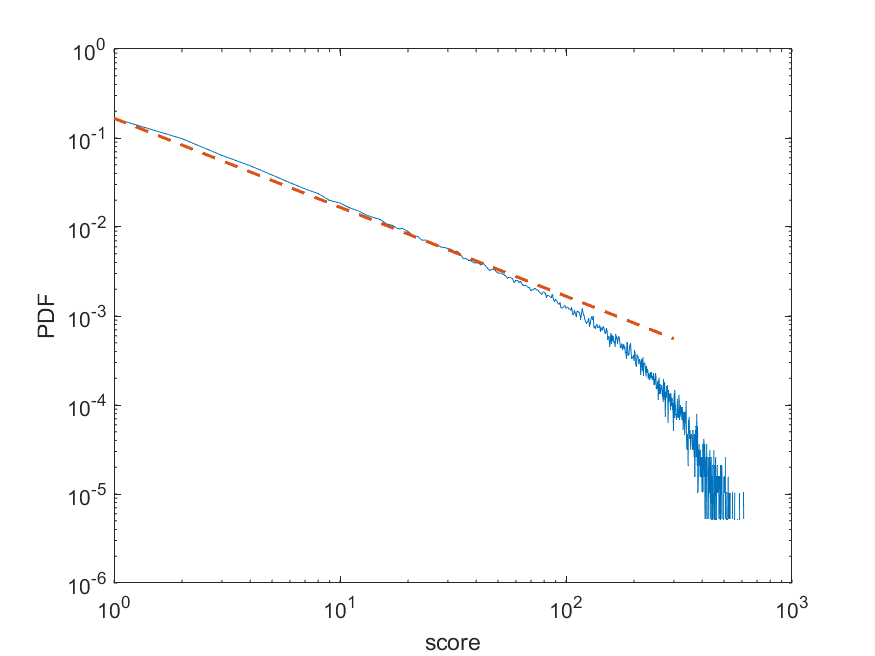
image

不难发现：

  • 得分较小（得分频率较高）时，得分与得分频率间存在幂律关系，且在双对数图下斜率大概是-1，也就是说：得分与得分频率间呈反比关系。
  • 得分较大（得分频率较低）时，得分与得分频率脱离幂律且向下弯曲。

对更多的尺寸进行模拟：

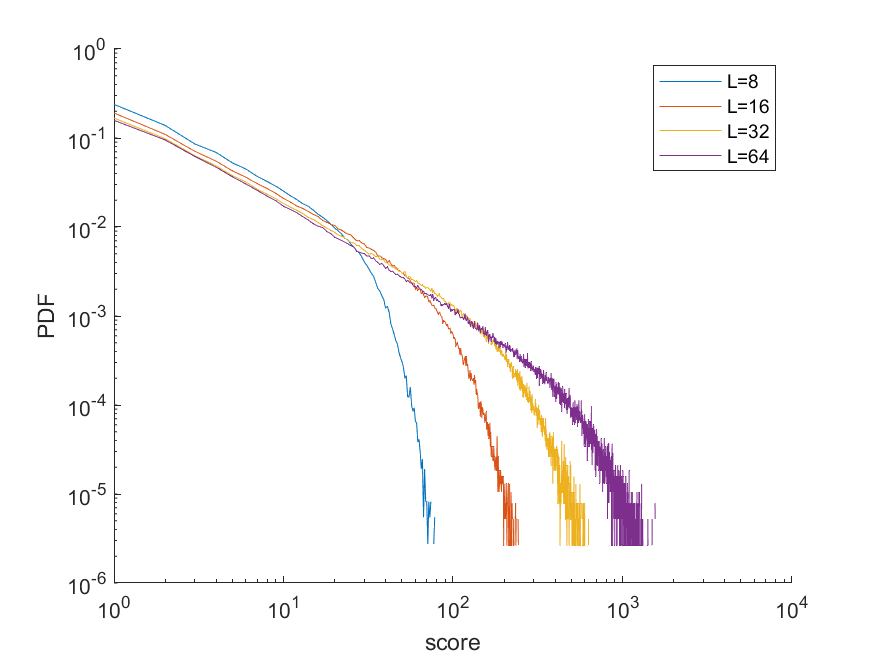
image

  • 得分与得分频率间存在幂律关系存在普适性，即随着尺寸的变化，仍然保持斜率为-1。
  • 随着尺寸的增加，幂律适用的范围增大，这可能与最大可得分的增加相关。

解释1：幂律不完全

显然不可能是完全的幂律，因为有限盘中理论最大的得分为

如果有完全的幂律，那么应该对应有无穷大的单次得分——这显然是不可能的，所以频率分布必须向最大得分弯曲，且终止于最大得分。可以自行模拟尺寸较小的情况验证。

解释2：幂律为-1

得分不大的情况下，引起一个4倍规模的频率可以用4次（也就是4倍频率）1倍规模的频率近似：

在$2L\times 2L$同时放四个的得分 $\approx$ 在$L\times L$放1个的得分$\times4$ $~\approx$ 在$2L\times 2L$放1个的得分$\times4$

这个可以导出(设f是频率随得分的函数)：

这是负一次齐次函数，对应的解只有反比函数（幂律且幂指数为-1）。证毕。

可以自行模拟验证第一个约等于号：在足够大的尺寸中同时投放四个方块，在一半的尺寸中投放单个方块的得分具有一定的比例关系。