题目

从不同的初值 $z_{0}$ 出发，牛顿法求解复方程 $z^{4} - 1 = 0$ 的根，并以一定的分辨率画出指定范围下不同初值的收敛结果:

1. $Re [z_{0}] \in (- 1, 1), Im [z_{0}] \in (- 1, 1)$ ，分辨率0.01

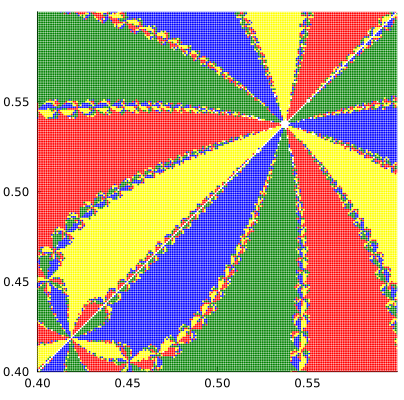
2. $Re [z_{0}] \in (0.4, 0.6), Im [z_{0}] \in (0.4, 0.6)$ ，分辨率0.001

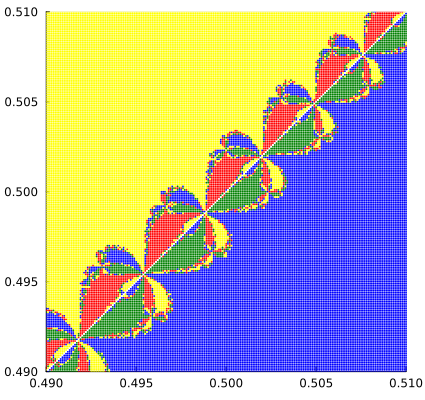
3. $Re [z_{0}] \in (0.49, 0.51), Im [z_{0}] \in (0.49, 0.51)$ ，分辨率0.0001

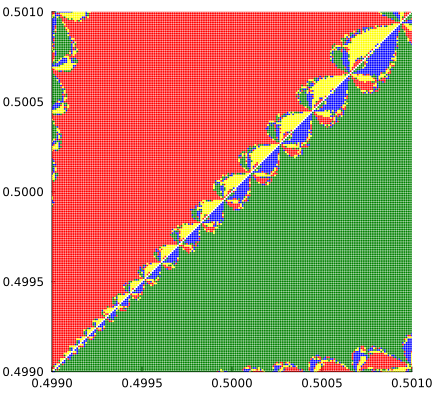
4. $Re [z_{0}] \in (0.499, 0.501), Im [z_{0}] \in (0.499, 0.501)$ ，分辨率0.00001

理论分析

方程 $z^{4} = 1$ 有四个解：

z_{1} = 1, z_{2} = - 1, z_{3} = 1 i, z_{4} = - 1 i

牛顿法的迭代方程为：

z = z - \frac{z^{4} - 1}{4 z^{3}} = \frac{3}{4} z + \frac{1}{4 z^{3}}

其中，分别对收敛到 $1, - 1, 1 i, - 1 i$ 的点染蓝色，红的，黄色和绿色。没有收敛的点为白色。

程序实现

julia

N=201
center=0
lim=1
xx=range(center - lim, center + lim; length = N)
yy = range(center - lim, center + lim; length = N)

X= repeat(xx, 1, length(yy))
Y = repeat(yy, 1, length(xx))'
p=4
Z=X+Y*im
Z_origin=Z

using Plots
cond=[1,-1,1im,-1im]
color=["blue","red","yellow","green"]
for i=1:4
    index=findall(x-> x<0.1,abs.(Z.-cond[i]))
    scatter!(real(Z_origin[index]),imag(Z_origin[index]),legend = false,xlim=(-1, 1), ylim=(-1, 1),color=color[i],ms=1,markerstrokewidth = 0)
end
plot!()
png("100")

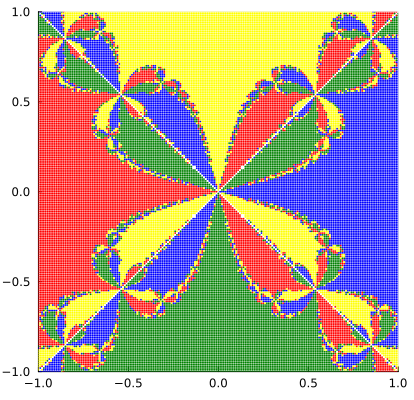
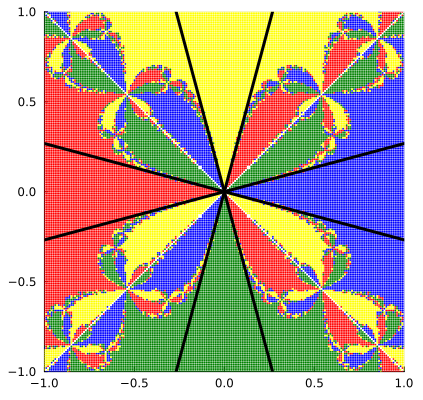
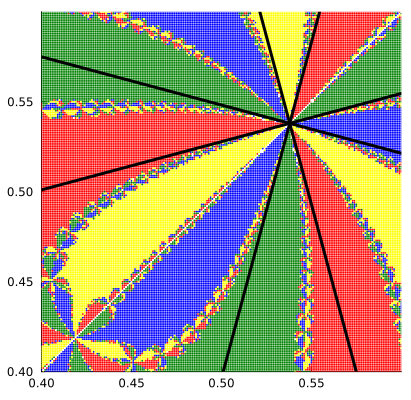
直观上看，可以发现：

四个单位根附近的初始点收敛到该单位根本身，而在直线 $y = \pm x$ 附近的初始点却不一定收敛到最近的单位根。
随着图像的放大，初始点的收敛情况呈现出分形的特征，且并非是一直收敛到同一单位根，颜色貌似和分形的指向有关。
直线 $y = \pm x$ 上的点不收敛
颜色区域由六条曲线分割，分别是 $y = \pm x$ ， $y = \pm (2 + \sqrt{3}) x$ ， $y = \pm (2 - \sqrt{3}) x$ ，