Quantum Dynamics & Quantum Geometry
薛定谔绘景
薛定谔方程描述了量子态随时间的演化:
或者使用时间演化算符$\hat{U}(t)=\exp[-\dfrac{it}{\hbar}\hat{H}]$表示为:
代入时间演化算符,可以获得简洁一般(不要求哈密顿量不含时)的薛定谔方程表达式:
薛定谔绘景描述了在确定的算符作用下,量子态的演化过程。
为了推导该方程的形式解,我们分以下三种情况:
- 哈密顿算符不依赖时间:则容易解出
- 哈密顿算符与时间相关,但不同时刻的哈密顿量算符对易:
- 哈密顿算符与时间相关,但不同时刻的哈密顿量算符不对易:
定态和叠加态
我们只考虑以上的第一种情况,那么时间算符同时与哈密顿算符对易,态矢量的演化可以用能量本征右矢表示:
所以不同的本征态会有不同的相位频率。这引出了定态的概念——定态是哈密顿算符的本征态。本征态的可观测量是不变的,而叠加态会变化。
自旋的进动
一个例子是自旋的进动。
可以得到:
只有当初始为定态时,其可观测量才不会变。
中微子振荡
海森堡绘景
对于唯一可测量的可观测量的平均值,时间演化相当于对其做幺正变换。我们发现似乎有两种方法来达到相同的目的,即
一种方法就是薛定谔绘景:
另一种方法就是海森堡绘景:
海森堡绘景认为算符是变化的,态右矢是固定的;既然算符是变化了,那么以某种算符产生的本征基右矢自然也是变化的:
海森堡运动方程
证明:
这里假定了算符不显含时间。
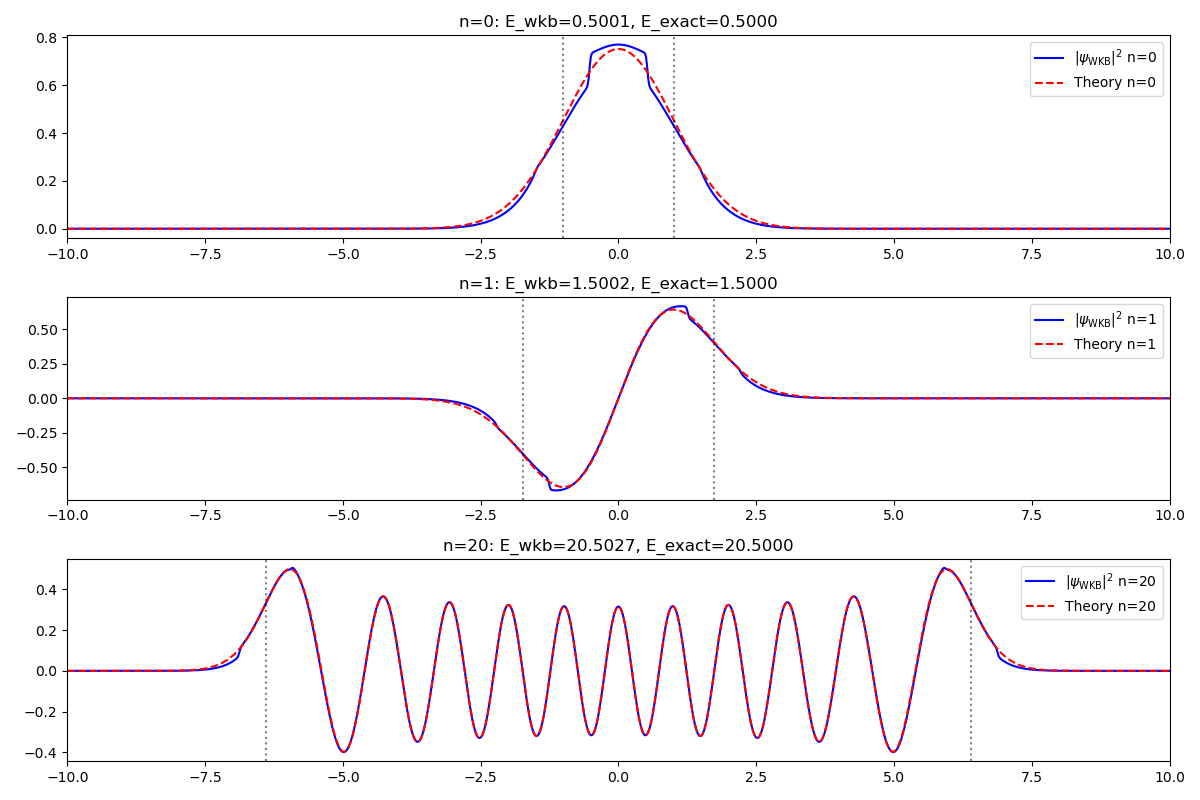
自由运动的粒子
考虑一个自由运动的粒子:
所以:
这意味着粒子的位置随着时间的推移越来越不确定,当然可以类比波动力学里自由粒子波包随时间的演化。
Ehrenfest定理
对于势场中的粒子:
简谐振子和相干态
简谐振子的模型可以阐述量子力学的诸多概念,如朗道能级、电磁场量子化、氢原子模型等等。
谐振子
一种计算两个算符之和的本征态的普遍的想法是:
处于朴素的理解,我们可以通过类比复数将哈密顿算符分解为:
其中$\hat a=\frac{1}{\sqrt{2\hbar m\omega}}(i\hat p+m\omega \hat x),\hat a^\dagger=\frac{1}{\sqrt{2\hbar m\omega}}(-i\hat p+m\omega \hat x)$。
然而并没有这么幸运,由于算符不对易,正确的结果应该为:
升降算符具有以下性质:
- 能级升降:
- 基态波函数:
- 升降系数:
- 其他本征函数:
- 反表示:
简谐振子动力学
根据运动方程:
同理
那么
然而由于其期望一直是0,能量本征态不能反应经典简谐振子的运动状态;能反应的其实是湮灭算符的本征态,即相干态。
相干态
湮灭算符的本征右矢定义为相干态:
由于湮灭算符不是可观测量,$\lambda$可以是任意复数。设$|\lambda\rangle=\sum_nC_n|n\rangle$,则
解得:
考虑归一化条件:
所以
位置表象
将相干态转移到位置表象:
其中:
所以
相应的概率为:
如果其随时间演化:
所以
其位置期望为:
与自由粒子波包不同,这个波包往复运动而不弥散。
粒子数算符
粒子数算符定义为:
作用在像相干态上:
某次测量得到N个光子的概率为:
这是个泊松分布。
幅值算符和相位算符
湮灭算符不是厄米算符,我们考虑:
其中幅值算符$\hat B$和相位算符$\hat \Phi$都是厄密算符。
由于$\hat a\hat a^\dagger=\hat N+1$,可设:
那么
之所以不取
是因为这样的话幅值算符就不存在逆算符了,因为对基态的本征值为0。
作用在能级上:
矩阵表示为:
相位算符定义为:
作用在能级上:
所以相位算符表示为:
相位算符的指数函数显然不是厄密的。定义三角函数部分:
可以证明:
朗道能级
经典理论
对于经典力学的方法,可以得到拉莫尔半径和频率:
对于分析力学:
如果还有电场:
假设电场朝x方向且磁场朝y方向,这可以解出:
这就是经典霍尔效应。
半经典量子理论
半经典近似指磁场未被量子化。磁场中的哈密顿量为:
遵循上述的分解方法:
其中
从$\hat a|0\rangle=0$可以解得:
设
得到基态波函数:
$f(z)$是任意函数,通常使用多项式函数近似:
其中
归一化条件给出:
简并
每一个n都对应了基态能量,所以对于无穷大体系,简并度无穷大。但是由于有限的面积A,此体系的简并度为
其中$\phi_0=\frac{h}{e}$是量子磁通,$\phi=AB$。
与我们物理直觉相符的是,朗道能级的简并度正比于磁场和面积。
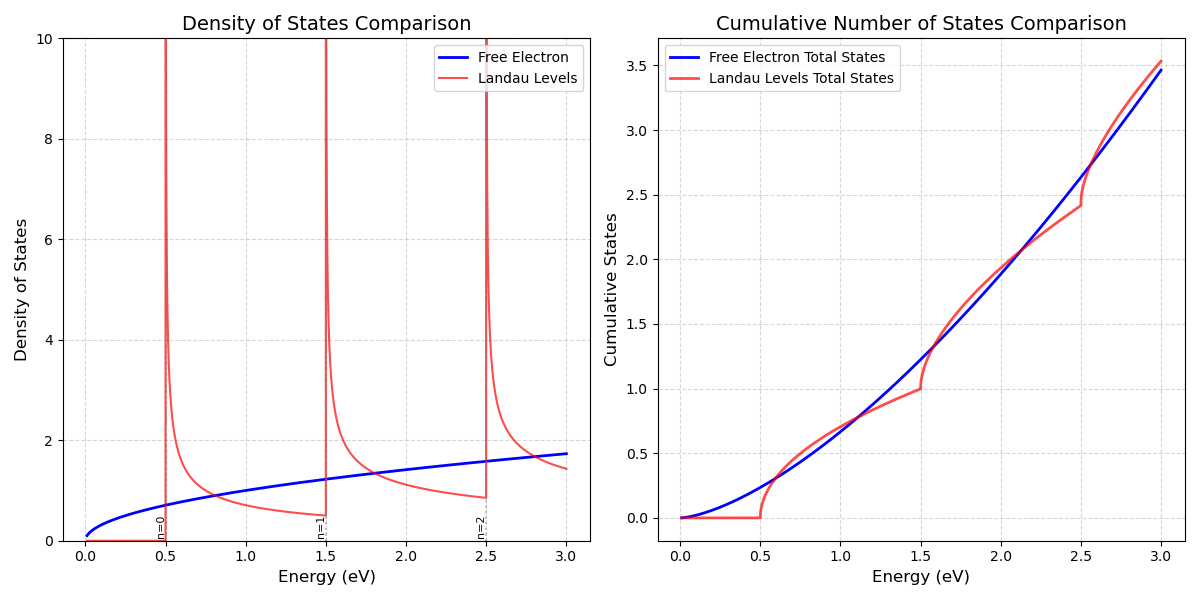
态密度
对于三维自由电子,其态密度为:
对于朗道能级,态密度可以视为一维自由电子($\vec{k}_z$方向)对量子数$n$的求和:
其中,一维自由电子的态密度由 近独立粒子的最概然分布 给出:
可以对三维自由电子在xy平面上积分后,与朗道能级的态密度比较:
import numpy as np |
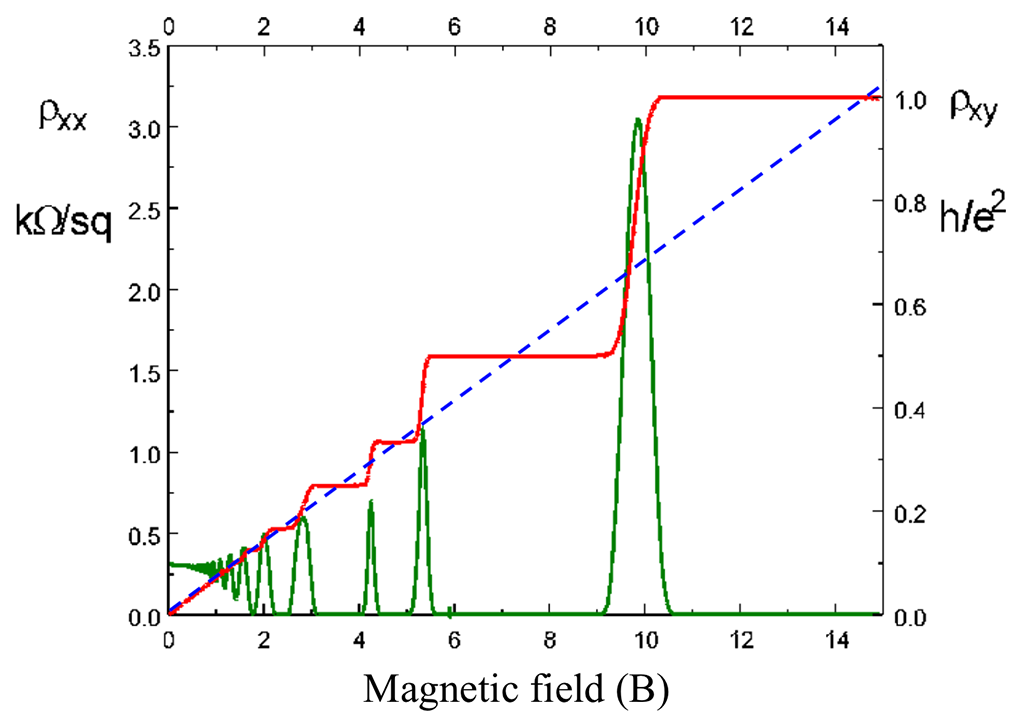
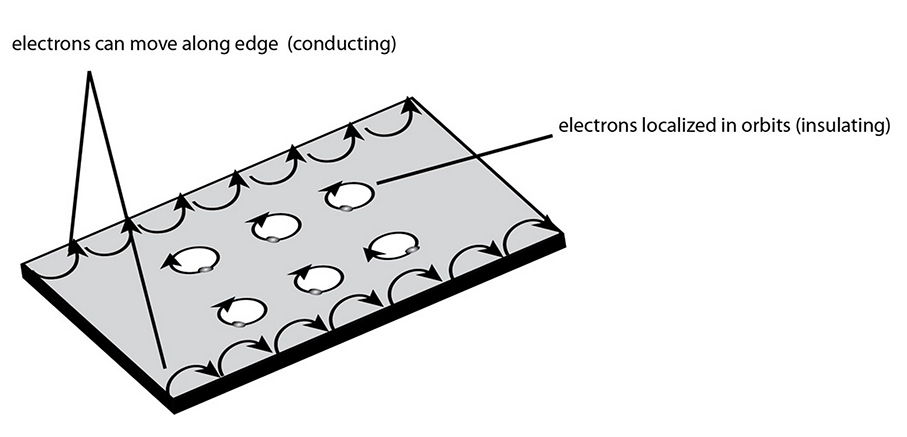
量子化霍尔电导
霍尔电阻定义为:
其中$V_y=E_y l=Blv$,$I_x=eNv$,所以
载流子浓度n与朗道能级总数N的关系:
霍尔电阻为:
其倒数定义为霍尔电导:
其中$\frac{e^2}{h}$是单位霍尔电导。
朗道提出用新的波函数:
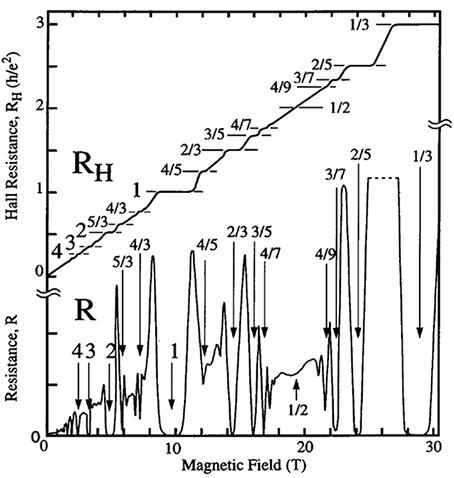
来描述分数霍尔效应,最后的结果为:
规范变换
规范变换的本意是对“标势和矢势进行的不影响电磁场和变换”。电矢势不是规范不变的,但是与磁矢势相关联的电磁场具有规范不变性。
现在,我们拓展规范不变性的概念:对于某些非可观测量做的规范变换可以使某些可观测量保持不变,或者可以是运动方程保持不变,这种不变性就是规范不变性。
- 全局规范变换:$\vec A\to \vec A+\vec{A_0},\phi\to \phi-\phi_0$
- 局域规范变换:$\vec A\to \vec A+\nabla\Lambda,\phi\to \phi-\frac{\partial\Lambda}{\partial t}$
标势的规范变换
考虑新增一个标势后的哈密顿量:
根据时间演化算符的定义:
代入即得:
矢势的规范变换
考虑新增电矢势后的哈密顿量:
计算时间的微商:
与前面的动量不同,我们称$\hat \Pi=\hat p-e\vec{A}$为机械动量,而把之前的$\hat p$称为正则动量。
更一般的情况
算符$\hat R$和算符$\hat P$组成所有其他算符,这两个算符是被规定的,他们不随规范的变化而变化:
但有些算符,比如$\phi,\vec{A}$是随着规范改变的。显然,显含$\phi,\vec{A}$的算符,比如哈密顿算符,随着规范变化。
态矢量的幺正变换
假设新的规范下,态矢量为$|\psi’\rangle$,那么:
这里需要用到坐标和机械动量的值不随规范改变,即
注意,值不随规范改变,不代表算符不随规范改变。
即:
从第一个式子得到:
从第二个式子得到:
综上,变换算符是:
薛定谔方程的规范不变性
将第二个式子展开:
所以:
因此我们知道,对哈密顿算符做以上规范变换可以保证薛定谔方程的规范不变性。具体来说,新的哈密顿算符为:
这刚好对应着:
概率和概率流密度的规范不变性
考虑:
所以:
所以
将$-i\hbar\nabla\rightarrow -i\hbar\nabla-e\vec{A}$之后,就可以证明概率流密度的规范不变性。
AB效应
考虑一个无限长的螺线管,磁通量为$\phi$,磁矢势为$\vec{A}=\frac{\phi}{2\pi r}\vec{e_\theta}$,从左右两侧通过的电子相差的相位为:
几何相位
绝热近似
我们考虑本征态变化即哈密顿量变化的情况:
考虑将态矢展开:
其中$|n(t)\rangle$是某组完备的本征态基矢。
代入薛定谔方程可得:
左边作用另一基矢$\langle m(t)|$:
绝热近似指,当哈密顿量变化缓慢的时候,$\langle m(t)|\dot{n}(t)\rangle$远小于1。
证明:对薛定谔方程求导:
左边作用另一基矢$\langle m(t)|$:
所以:
证毕。
这样我们可以对方程进行进一步的化简:
解得:
我们知道前一项是动力学相位,后一位被定义为几何相位:
其中
当然,如果引起本征态或哈密顿算符变化的参数不直接是时间而是$\lambda(t)$,原定义推广为:
其中$\vec{A}=i\langle m(\lambda(t))|\vec{\nabla_\lambda}|m(\lambda(t))\rangle$被称为贝里联络,具有类似于电矢势的物理意义。而$\vec{B}=\nabla\times\vec{A}$被称为贝里曲率,具有类似于磁场的物理意义。
| 实空间 | AB相位 | 电矢势 | 磁场 |
| 参数空间 | 贝里相位 | 贝里联络 | 贝里曲率 |
重新计算AB相位,通过规范变换可得:
取$\nabla\Lambda=\vec{A},\dot\Lambda=0$,则:
换句话说:
贝里联络为:
用到了定态下物理期望为0的条件。
例子:无限深势阱边界的移动
在坐标表象下:
注意到没有关于L的平方项,在闭合回路积分中等于0。
例子:自旋1/2的磁矩
相应的本征态为:
取向上态,贝里联络为:
所以贝里联络为:
贝里曲率:
量子几何
经典度规
两点之间的距离表示为:
其中,$g_{\mu\nu}$是经典度规,常见的度规有:
- 直角坐标系:
- 极坐标系:
- 球坐标系:
量子度规
假设量子态依赖于$\lambda$:
通过内积的方式来度量两个量子态的距离:
如果我们要求其模方,那么对每一项的实虚分辨是必要的。分析:
- 第二项$\langle \psi(\lambda)|\partial_\mu|\psi(\lambda)\rangle$是纯虚的,因为:
- 第三项$\partial_\mu\langle \psi(\lambda)|\partial_\nu|\psi(\lambda)\rangle$是纯虚的,即$\langle \partial_\mu\psi(\lambda)|\partial_\nu\psi(\lambda)\rangle+ \langle\psi(\lambda)|\partial_\mu\partial_\nu|\psi(\lambda)\rangle$,那么记$r_{\mu\nu}\equiv \Re\psi(\lambda)|\partial_\mu\langle\partial_\nu|\psi(\lambda)\rangle$
那么可以表示为:
所以$g_{\mu\nu}=r_{\mu\nu}-A_\mu A_\nu$就是量子度规。可以推广为量子几何张量
那么量子度规就是量子几何张量的实部,其虚部是贝里曲率:
综上: