题目

1.对于迭代方程$x_{n+1}=1-\mu x_n^2$，分析不同$\mu\in (0,2)$下$x_n$的长时间行为，及其与初值$x_0\in(-1,1)$的关系。

2.对于迭代方程$f(x)=\left\{\begin{aligned}
x_{n+1}=1-\mu x_n & x>0\\
x_{n+1}=1+\mu x_n & x<0
\end{aligned}
\right.$，分析不同$\mu\in (0,2)$下$x_n$的长时间行为，及其与初值$x_0\in(-1,1)$的关系。

3.对于迭代方程$x_{n+1}=1-\mu x_n$，分析不同$\mu\in (0,2)$下$x_n$的长时间行为，及其与初值$x_0\in(-1,1)$的关系。

4.比较上述两种情况，你发现了什么。

如果你有幸在物理实验课上进行了混沌相关的实验，你会发现这就是实验课所讲的虫口模型：虫子在繁殖增加和竞争减小的双重作用下，数量产生了周期性或非周期性的波动。研究其中的行为特征，可以对混沌理论和行为略窥一二。

这里仅针对第一种情况进行以下方面的讨论。

初步理论分析

良好的理论分析可以减少不必要的尝试。对于$x_{n+1}=1-\mu x_n^2$，显然在该初值和系数范围下，$x_n$的绝对值不会超过1，那么不必担心发散的问题。

程序实现对单一系数初值组合的行为

%% Parameter
mu=0.5;
x0=0;
cir=500;
x=zeros(1,cir+1);
x(1)=x0;

%% Main
for i=1:cir
    x(i+1)=1-mu*x(i)^2;
end

%% Plot
figure
plot(x)

以此为基础，稍作修改即可对不同的系数初值组合进行模拟。

对$\mu$的讨论

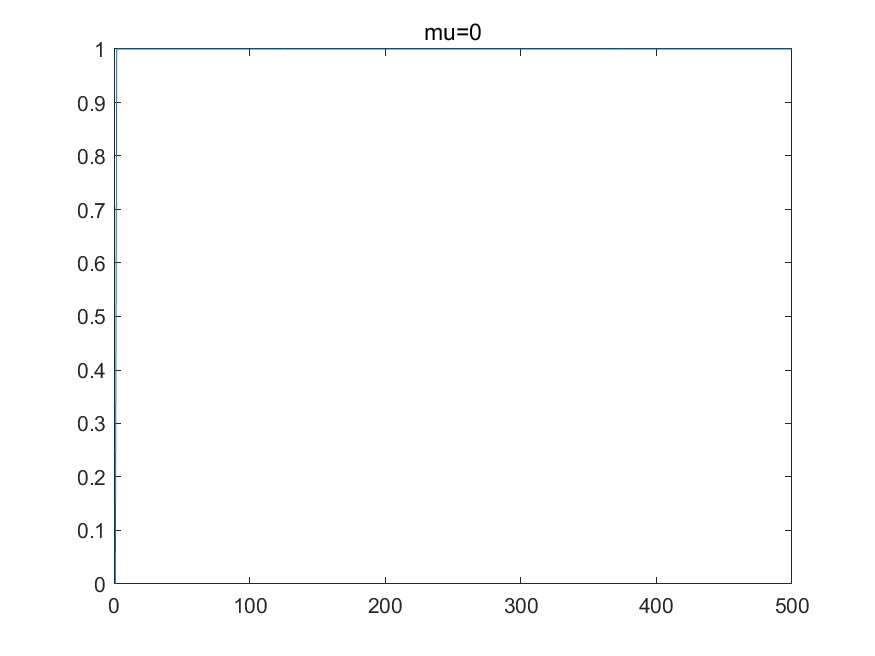
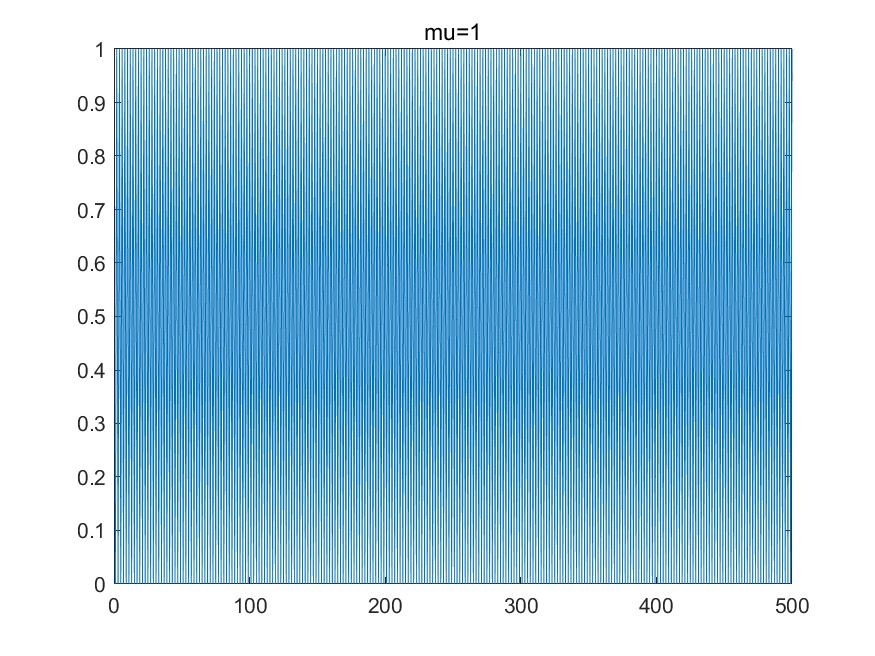
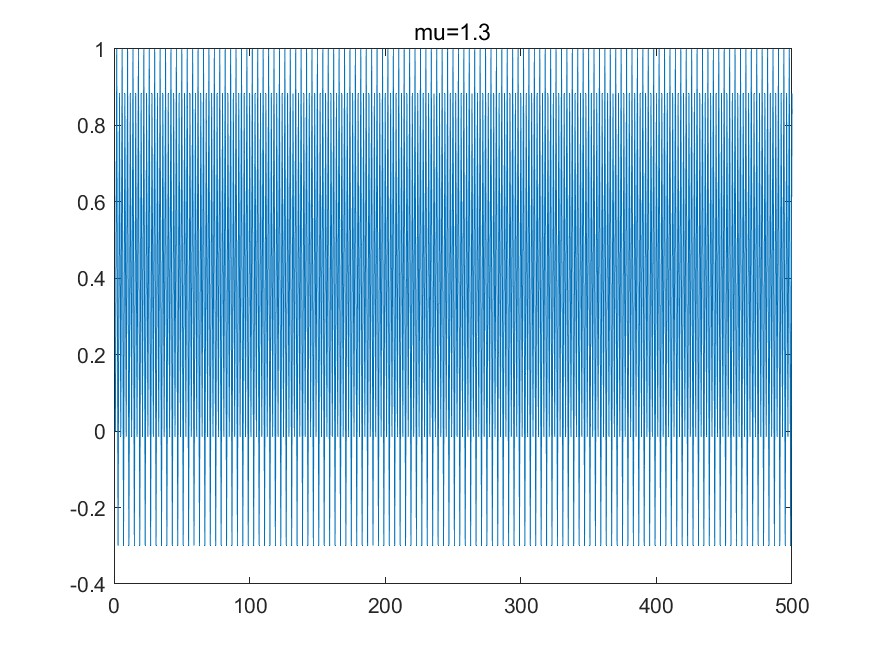
从$x_0=0$，$\mu=0,1,1.3,1.6$开始，绘制500次迭代的图像如下，此时部分图像已出现稳定情况，可视为长时间行为：

  • 当$\mu=0$时，图像稳定于$x_n=1$。
  • 当$\mu=1$时，图像稳定于$x_n=0,1$，出现二周期震荡（周期为2）行为。
  • 当$\mu=1.3$时，图像有四个稳定点，出现四周期行为。
  • 当$\mu=1.6$时，图像出现不规则震荡和混沌现象。

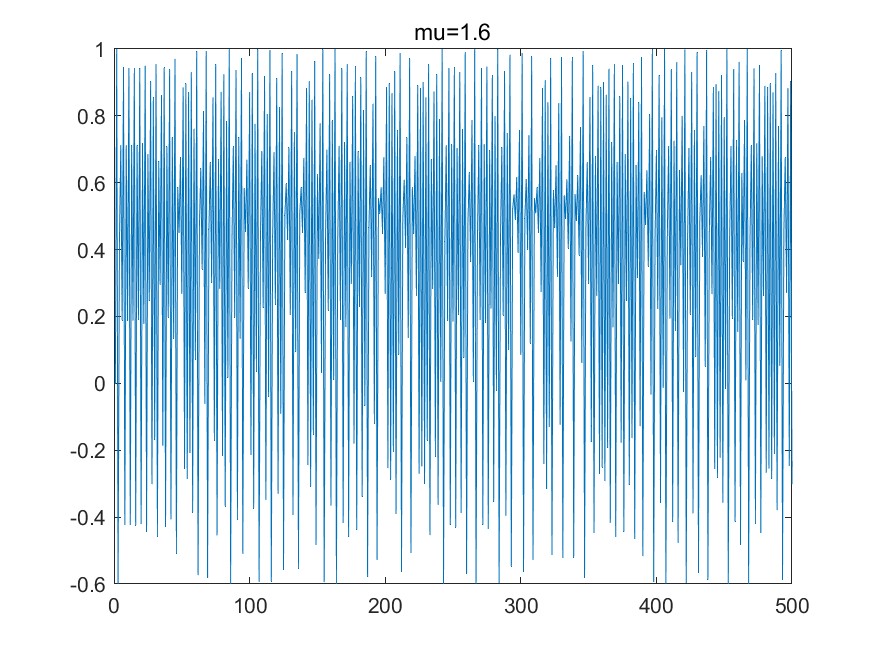
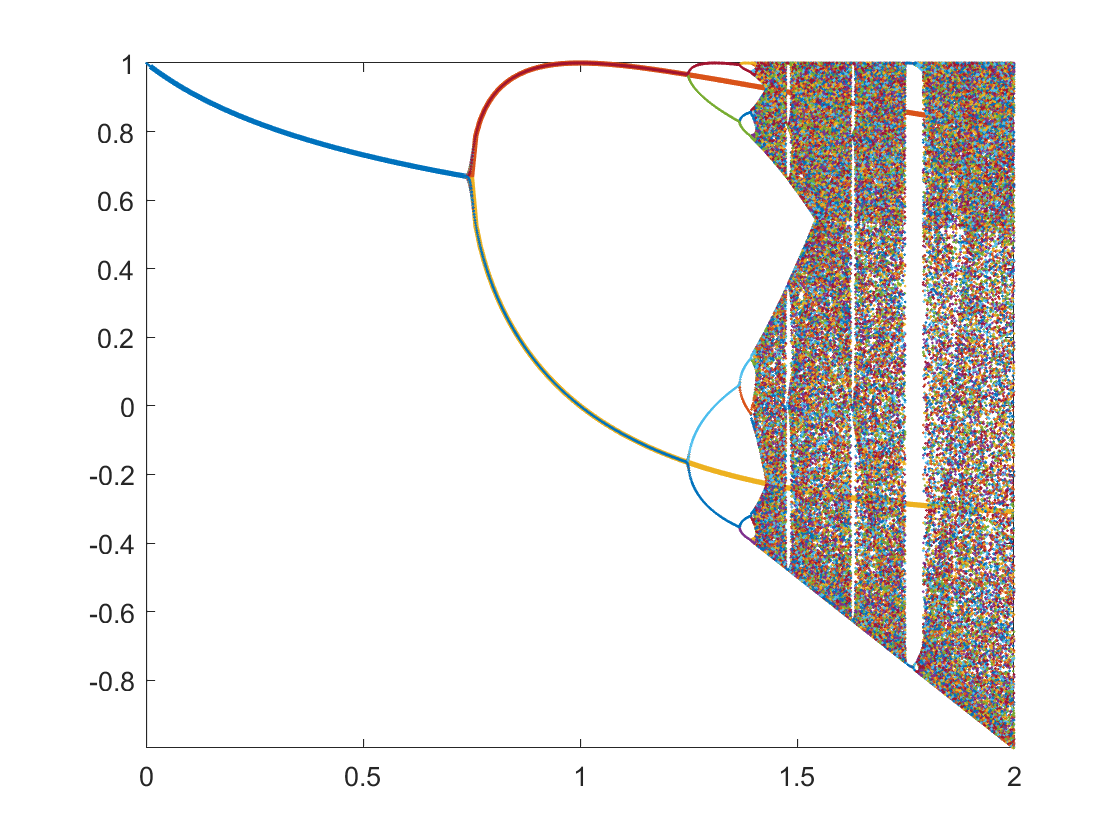
image

image

image

image

不难发现，稳定点常表现为极值点，在$x_0=0$的条件下，找出稳定后图像中的极值点并绘制出极值点-$\mu$值的关系图像。

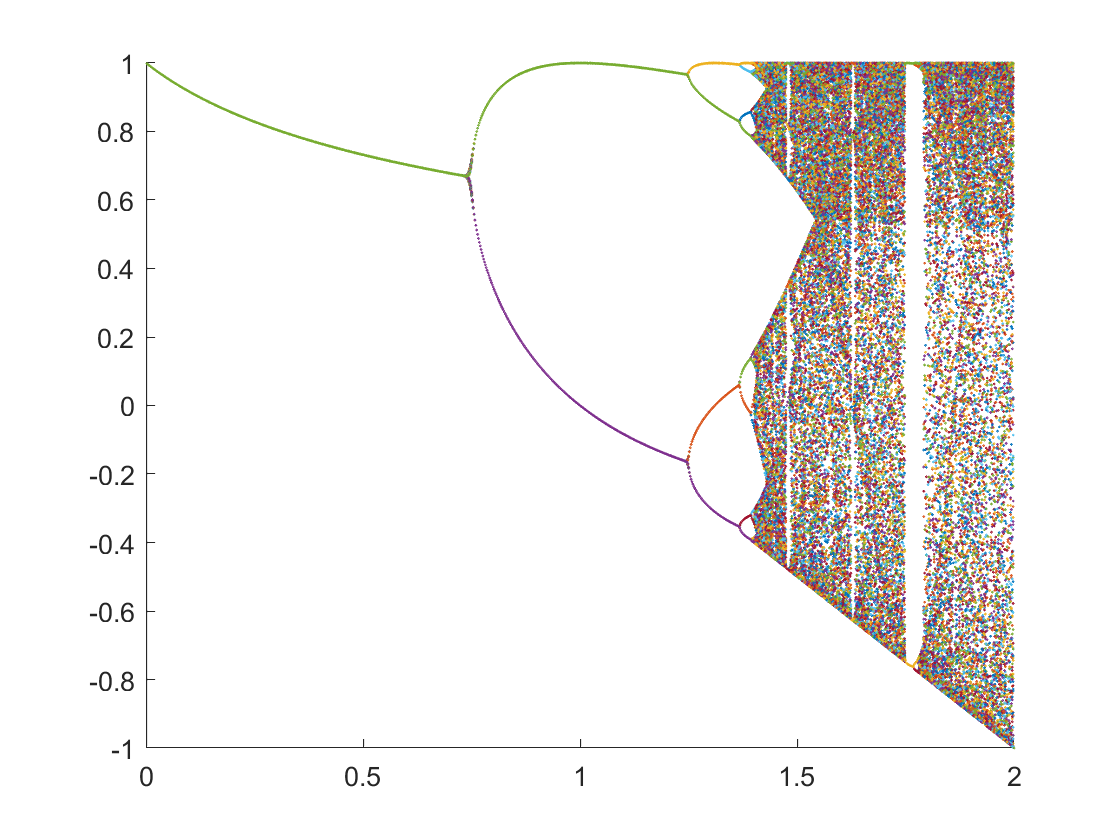
image

该图像说明，当$\mu$从小增大，图像由稳定逐步过渡到二周期震荡，四周期震荡...再过渡到混沌。每个$\mu$值对应的周期数和震荡点理论上都可以通过方程迭代解出（具体讨论见问题三）。

与$x_0$的关系

稳定点实质是方程的不动点(于问题三中讨论)，这说明其行为和初值关系不大。然而当出现混沌的时候，初值的变化会导致后续迭代的显著不同，这本身是混沌的定义。

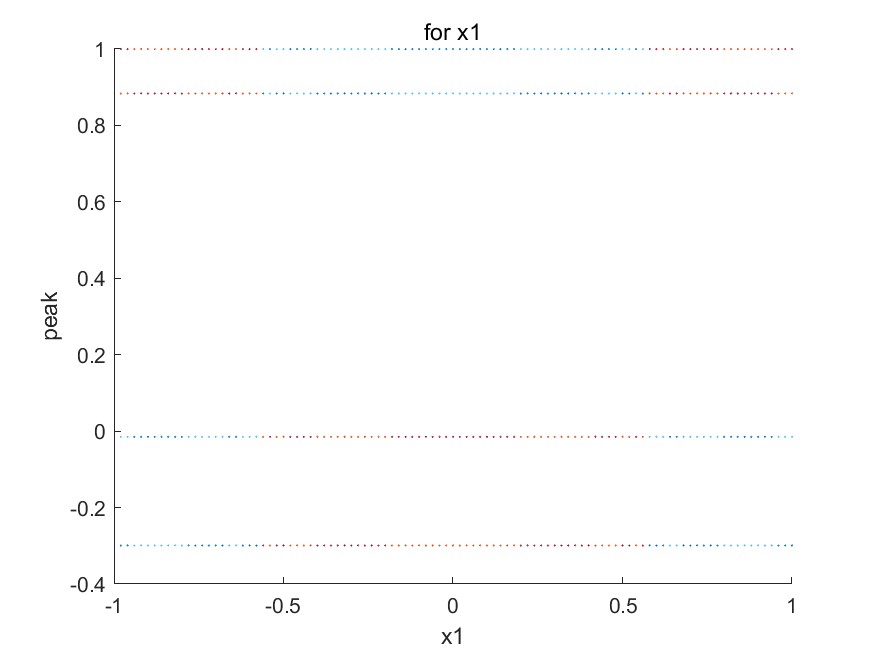
当方程本身存在稳定的周期震荡的时候，初值的变化不影响其长时间行为。绘制极值点-$x_0$图像如下（$\mu=0,1,1.3$）：

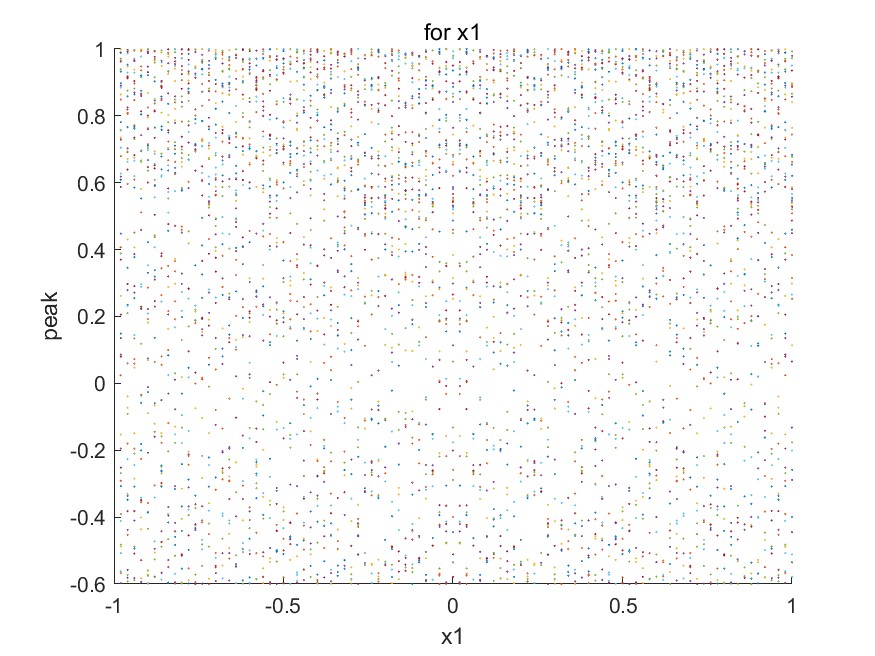
image

image

image

当方程本身无规则震荡的时候，初值的变化极易影响长时间行为：

image

将两个图像合并到一个三维图里面：

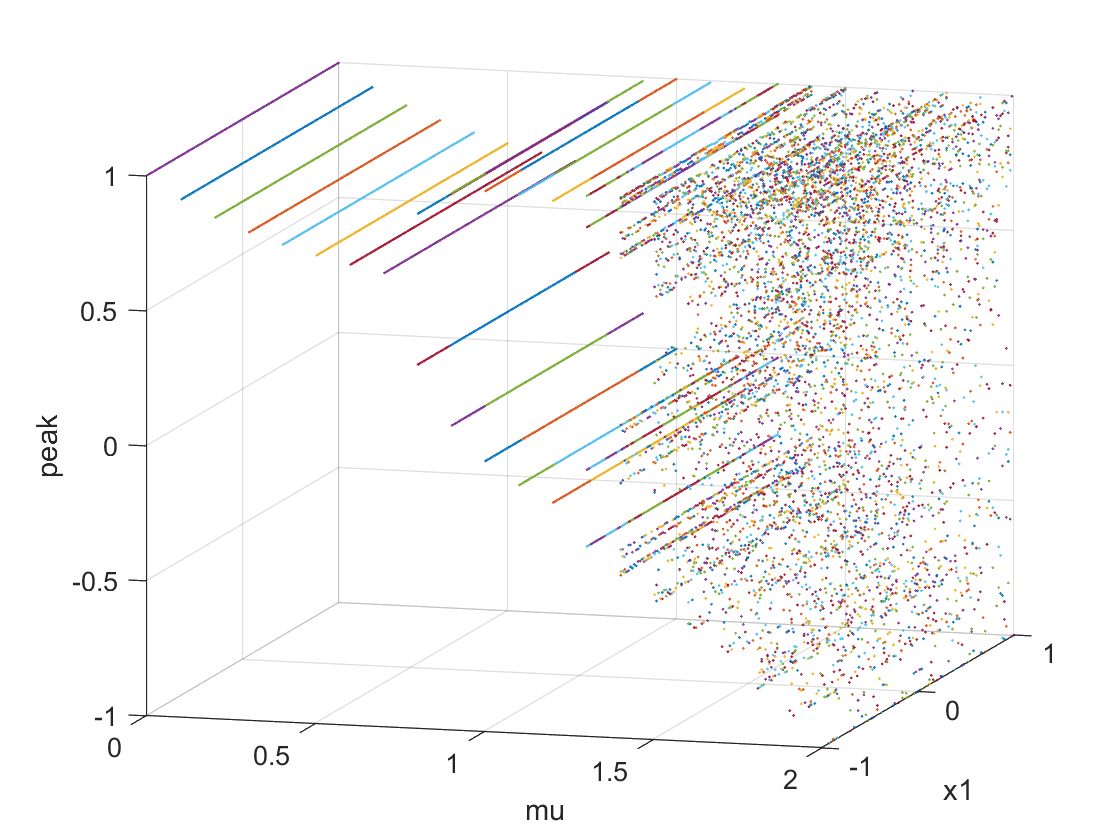
image

所以，迭代方程$x_{n+1}=1-\mu x_n^2$的长时间行为应是：长时间震荡行为趋于周期运动，并随着$\mu$增大周期增倍，此时与$x_0$几乎无关（除了会在对应的$\mu$处”合拢”，直至出现混沌，此时$x_0$的变化极易影响震荡行为。

稳定点与分叉

不难发现，不管是$x_{n+1}=1-\mu x_n^2$还是$x_{n+1}=1-\mu x_n^4$，
都存在稳定点和分叉结构和混沌现象。

稳定点是由于方程的不动点形成的。以前者为例，稳定情况即方程本身的不动点(不稳定解已舍去)：

二周期震荡是迭代方程和二阶不动点：

将理论解和真实情况同时画在图中，可见是相差无几的：

image

不动点的稳定性

以下方程实际上有两个根，为何其中一个是不稳定的？

image

不妨计算方程右边在不动点处的斜率：

由蛛网图不难得知，斜率大于1者不稳定而小于1者稳定，这也是为什么舍去另一个解（$\frac{-1-\sqrt{1+4\mu} }{2\mu}$）的原因。当$\mu>0.75$时，原本的稳定解对应的斜率也大于1，也变得不稳定。

image

image

对高阶不动点的分析同理。

有兴趣的同学可以搜索费根鲍姆常数，并通过该模型计算该常数的数值。