费米加速机制

• 直碰的乒乓球模型
• 随机角度的乒乓球模型
• 随机角度的乒乓球流模型
• 天文情况的概论
• Shock-Fermi I
• Cluster-Fermi II
• 数值讨论
• 能量增加率分布
• 更详细的推导
• 无穷小速度场与平均速度场
• 扩散模型

在研究并和星系团的大尺度射电晕结构时，经常用到的解释时费米的一二阶加速，其本质上是预加速电子在星系团湍流的作用下的统计上的能量增加。

费米一阶加速预期电子被激波加速，看上去就好像电子被激波反弹了回来，从而获得了加速的能量。从下面这样一个简单的模型可以略窥一二。

直碰的乒乓球模型

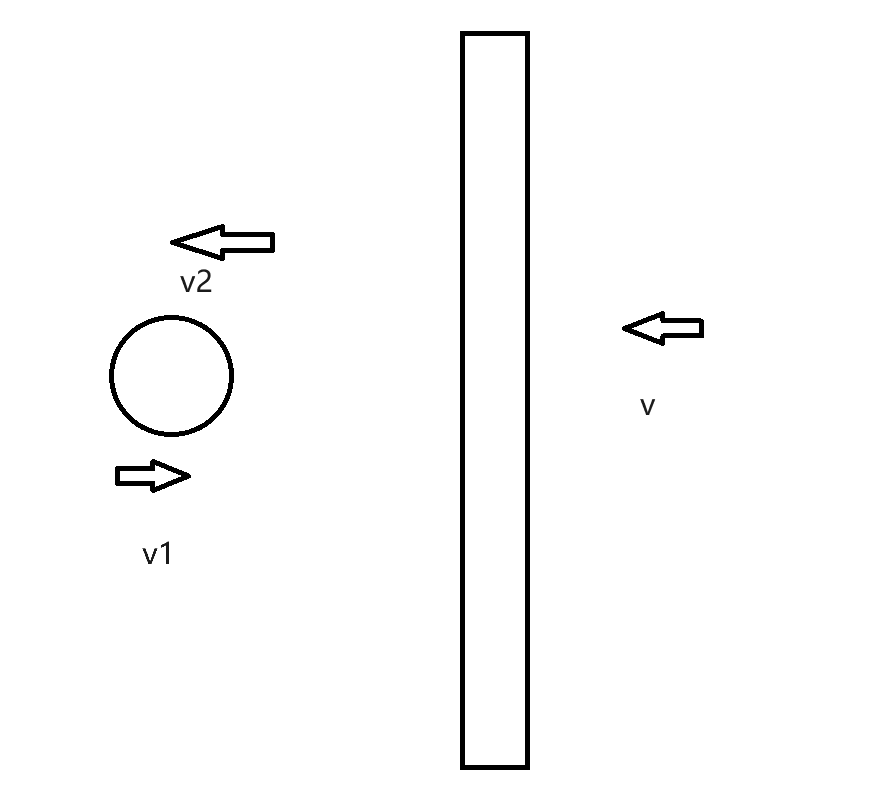
墙的速度为$v$，小球碰前速度为$v_1$，碰后速度为$v_2$。满足墙坐标系下能量守恒：

$$v_1+v=v_2-v\Rightarrow v_2=v_1+2v$$

能量的增加为：

$$\Delta E=\frac12 m(v_1+2v)^2- \frac12 mv_1^2=2m(v_1v+v^2)$$

能量增加率为：

$$\epsilon=\frac{\Delta E}{E}=4\frac{v_1v+v^2}{v_1^2}\approx 4\frac{v_1}{v}$$

近似采用了墙的速度$v$远小于球的速度$v_1$。此时，可以看到整体为一阶加速，即能量增加率和墙的速度的一阶呈正比。

随机角度的乒乓球模型

$$\Delta E=\frac12 m(v_1+2v\cos{\theta})^2- \frac12 mv_1^2=2m(v_1v\cos{\theta}+v^2\cos^2{\theta})$$

能量增加率为：

$$\epsilon=\frac{\Delta E}{E}\approx 4\frac{v_1\cos{\theta}}{v}$$

考虑到$\theta$角度的随机性：

$$\langle\epsilon\rangle\approx 4\frac{v_1}{v}\langle\cos{\theta}\rangle$$

对于单个球，$\theta$的权重与对应的面积元呈正比，那么：

$$weight \propto dS=d(2\pi R (1-\cos{\theta}))=2\pi R \sin{\theta}d\theta\propto\sin{\theta}d\theta$$

积分得到：

$$\langle\cos{\theta}\rangle=\frac{\int_{0}^{\frac\pi2}\cos{\theta}\sin{\theta} d\theta}{\int_{0}^{\frac\pi2} \sin{\theta}d\theta} =\frac{1}{2}$$ $$\langle\epsilon\rangle\approx 2\frac{v_1}{v}$$

可见，角度的随机不影响加速机制的阶数。

随机角度的乒乓球流模型

我们考虑到并非是单个的球，而是球的“流”(flux)。对于流，$\theta$的权重与碰撞事件数呈正比，事件数与对应的面积元和相对速度呈正比，那么：

$$weight \propto dn=(v_1\cos{\theta}+v)dS\approx v_1\cos{\theta}dS=2\pi R v_1\cos{\theta}\sin{\theta}d\theta$$

积分得到：

$$\langle\cos{\theta}\rangle=\frac{\int_{0}^{\frac\pi2}\cos^2{\theta}\sin{\theta} d\theta}{\int_{0}^{\frac\pi2}\cos{\theta} \sin{\theta}d\theta} =\frac{2}{3}$$ $$\langle\epsilon\rangle\approx \frac{8}{3}\frac{v_1}{v}$$

天文情况的概论

天文情况和球模型不同之处在于：粒子往往是相对论粒子；激波或星系团往往被假定为无穷大质量；粒子在激波或星系团坐标系下能量守恒的原因来自于“弹性碰撞”，这是通过磁场造成的。

此处隐含的假定：

1. 粒子不与其他粒子碰撞；

2. 由于云团的速度远小于粒子的速度，所以$\gamma$接近1，忽略以下变化：

   • 参考系变化前后的夹角很小
   • 参考系变化前后的磁场产生的电场很小（最大0.01V/m）

3. 磁场是时缓变的（不然会产生强电场）；

4. 磁场也是空间缓变的（不然磁矩会变）。

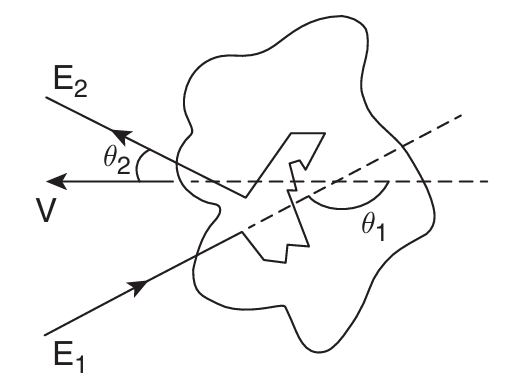
洛伦兹变换的公式为：

$$\begin{array}{l}E^{\prime}=\gamma(E-\vec{v}\cdot\vec{p})\\\vec{p^{\prime}}=\gamma(\vec{p}-\dfrac E{c^2}\vec{v})\end{array}$$

考虑粒子原来的四动量$(E_0,\vec{p_0})$，激波或星系团的速度为$v$，洛伦兹变换后的四动量为：

$$E_1^*=\gamma(E_1-v p_1\cos{\theta_1})$$

出射能量为：

$$E_2=\gamma(E_2^*+v p_2^*\cos{\theta_2})$$

在云团参考系中能量守恒，所以：

$$E_2^*=E_1^*$$

由于是相对论粒子，其能量

$$E^2=p^2c^2+m_0^2c^4\approx p^2c^2$$

记$\beta=\dfrac vc$，则

$$E_1^*\approx\gamma E_1(1-\beta \cos{\theta_1})$$ $$E_2=\gamma E_1^*(1+\beta \cos{\theta_2})=\gamma^2E_1(1+\beta \cos{\theta_2})(1-\beta \cos{\theta_1})$$

能量增加率为

$$\epsilon=\frac{\Delta E}{E}= \gamma^2(1+\beta \cos{\theta_2})(1-\beta \cos{\theta_1})-1=\frac{\beta(\cos{\theta_2}-\cos{\theta_1})-\beta^2(\cos{\theta_2}\cos{\theta_1}-1)}{1-\beta^2}$$

Shock-Fermi I

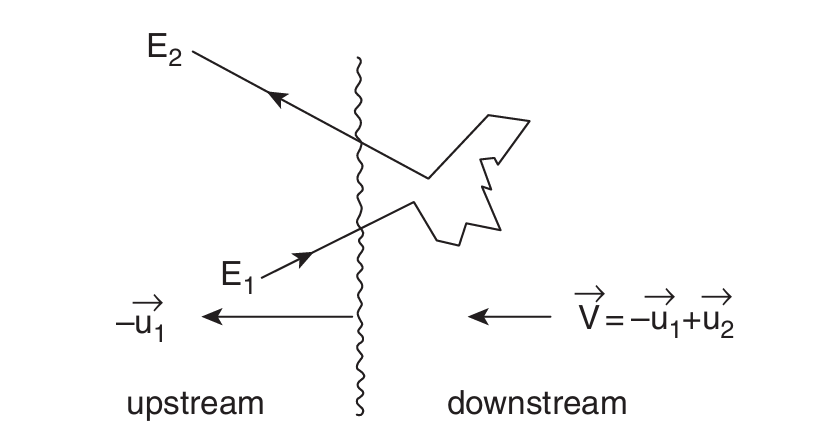
这种情况像乒乓球，

$$\langle\cos{\theta}\rangle=\frac{2}{3}$$

所以

$$\langle\cos{\theta_1}\rangle=-\frac{2}{3},\langle\cos{\theta_2}\rangle=\frac{2}{3}$$

能量增加率为

$$\langle\epsilon\rangle= \frac{\frac43\beta+\frac{13}{9}\beta^2}{1-\beta^2}\approx\frac43\beta$$

Cluster-Fermi II

注意到，星系团云团允许从后往前入射（快追慢，导致$\theta_1$取值范围变化），也允许从前穿射到后方（导致$\theta_2$取值范围变化）。

这里采用一种更简单的方法，将星系团看成两面激波，从前面入射穿射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(-\frac23+\frac23)+\beta^2(1-\frac49)}{1-\beta^2}$$

从前面入射反射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(+\frac23+\frac23)+\beta^2(1+\frac49)}{1-\beta^2}$$

从后面入射穿射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(+\frac23-\frac23)+\beta^2(1-\frac49)}{1-\beta^2}$$

从后面入射反射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(-\frac23-\frac23)+\beta^2(1+\frac49)}{1-\beta^2}$$

所以总的能量增加率为四者之和，一阶项被抵消

$$\langle\epsilon\rangle= \frac{\beta^2}{1-\beta^2}\approx \beta^2$$

二阶费米机制的来源是一阶费米机制的相消，\textbf{一阶项抵消，只留下二阶项}。

如果进行更精确的计算，那么迎头撞和追尾撞的事件数是不一样的（这是由于追尾撞的相对速度较低）

$$weight \propto dn=(v_1\cos{\theta}+v)dS\propto(v_1\cos{\theta}+v)\sin{\theta}d\theta$$

补正如下：

$$\langle\cos{\theta_1}\rangle=\frac{\int_{0}^{\frac\pi2}\cos{\theta}(v_1\cos{\theta}+v)\sin{\theta} d\theta}{\int_{0}^{\frac\pi2} (v_1\cos{\theta}+v)\sin{\theta}d\theta} \approx\frac{\frac13v_1+\frac12 v}{\frac12 v_1+v}=\frac{2}{3}+\frac13\beta$$

从前面入射穿射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(-\frac23+\frac23+\frac13\beta)+\beta^2(1-\frac23(\frac{2}{3}+\frac13\beta))}{1-\beta^2}$$

从前面入射反射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(+\frac23+\frac23+\frac13\beta)+\beta^2(1+\frac23(\frac{2}{3}+\frac13\beta))}{1-\beta^2}$$

从后面入射穿射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(+\frac23-\frac23+\frac13\beta)+\beta^2(1-\frac23(\frac{2}{3}-\frac13\beta))}{1-\beta^2}$$

从后面入射反射的能量增加率为

$$\langle\epsilon\rangle= \frac{\beta(-\frac23-\frac23+\frac13\beta)+\beta^2(1+\frac23(\frac{2}{3}-\frac13\beta))}{1-\beta^2}$$

很容易看出，抛开三阶项，只比上述计算多出了$\frac13\beta^2$，所以最终的结果为

$$\langle\epsilon\rangle= \frac43\beta^2$$

数值讨论

一般而言，对于星系团中的湍流，$v\sim10km/s,\beta=10^{-4}$，每次二阶加速的能量增加率为：

$$\langle\epsilon\rangle= 10^{-8}$$

如果我们假定云团的尺寸为1pc，粒子在里面运动的时间为10年量级($3\times 10^8 s$)，粒子的速度为$\gamma=10^3$，磁场平均大小为$1\mu G$，拉莫尔半径取$1.7\times 10^7 \gamma\approx10^{10}m$，同步辐射的功率为

$$P=\frac23\frac{e^2a^2\gamma^4}{c^3}\approx 10^{-30}J/s$$

那么在10年内，粒子加速一次，平均加速功率为：

$$P_{acc}=\gamma mc^2\beta^2\approx10^{-19}J/10yr\approx 3\times 10^{-27}J/s$$

这样算下来，加速完全是有可能的。

需要注意的是，为什么可以用平均能量增加率来计算，这是因为：

$$\epsilon_{final}=\prod_{i=1}^n(1+\epsilon(i))^n\approx1+\sum_{i=1}^n \epsilon(i)=1+n\langle\epsilon\rangle$$

能量增加率分布

幸运的是，尽管$\theta$满足正弦分布，其$\cos$值满足均匀分布，那么能量增加

$$\epsilon=\frac{\beta(\cos{\theta_2}-\cos{\theta_1})-\beta^2(\cos{\theta_2}\cos{\theta_1}-1)}{1-\beta^2}$$

的分布就可以理论计算出来，即

$$\epsilon\sim \beta\times TriangleDistribution(x|-2,2,0)+\beta^2(1-\frac12\ln(|x|)),x\in [-1,1]$$

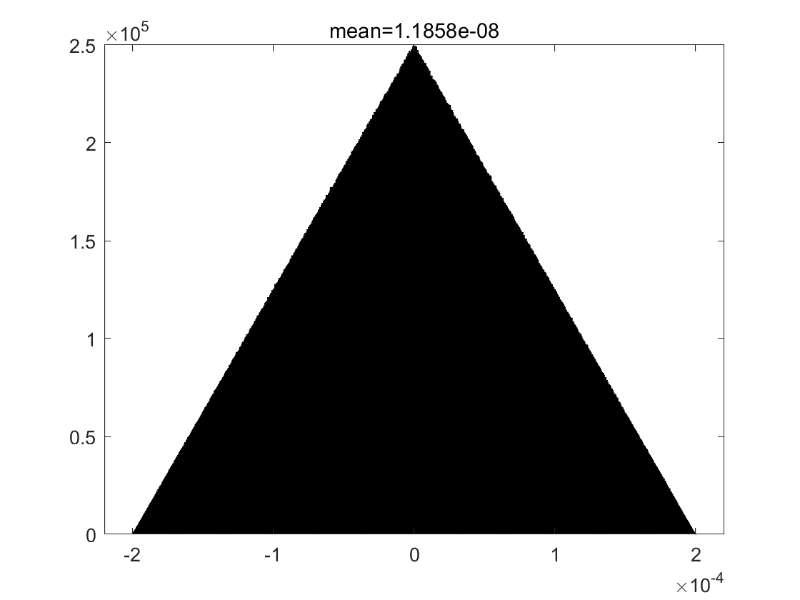
更详细的推导

能量增加率表达式为：

$$\epsilon=\frac{\Delta E}{E}= \gamma^2(1+\beta \cos{\theta_2})(1-\beta \cos{\theta_1})-1=\frac{\beta(\cos{\theta_2}-\cos{\theta_1})-\beta^2(\cos{\theta_2}\cos{\theta_1}-1)}{1-\beta^2}$$

这个式子的谬误在于，当$\theta_1=\theta_2$的时候，能量是增加的，这是反直觉的，因为粒子根本没有受到偏转。

这里的谬误原因是：相对论变换前后夹角发生了改变。我们对以上谬误进行debug，如果对同一个粒子进行变换后反变换，那么其能量为：

$$E_1=\gamma(\gamma(E_1-vp_1\cos{\theta_1})+vp_1^*\cos{\theta_1^*})$$

谬误的产生源于直接让$\theta_1=\theta_1^$，$p_1=p_1^$，如果这样做，那么：

$$\begin{aligned} E_1&=\gamma(\gamma(E_1-vp_1\cos{\theta_1})+vp_1\cos{\theta_1})\\ &=\gamma^2 E_1+vp_1\cos{\theta_1}(\gamma-\gamma^2)\\ \Leftrightarrow E_1(\gamma^2-1)&=vp_1\cos{\theta_1}(\gamma^2-\gamma) \end{aligned}$$

这显然是不对的。对于动量和角度的变换，以下给出公式：

$$p_1^*=\gamma(p_1-\frac{vE}{c^2}\cos{\theta_1})=\gamma p_1(1-\beta\cos{\theta_1})$$ $$\cos{\theta_1^*}=\cos{\theta_1}-\dfrac{vE}{p_1c^2}\sin^2{\theta_1}=\cos{\theta_1}-\beta\sin^2{\theta_1}$$

我们用新的公式严格进行上面的正反变换：

$$\begin{aligned} E_1&=\gamma(\gamma(E_1-vp_1\cos{\theta_1})+vp_1^*\cos{\theta_1^*})\\ \Leftrightarrow \gamma^2\beta^2E_1&=\gamma v(\gamma p_1\cos{\theta_1}-p_1^*\cos{\theta_1^*})\\ \Leftrightarrow\gamma^2\beta^2E_1&=\gamma v(\gamma p_1\cos{\theta_1}-\gamma p_1(1-\beta\cos{\theta_1})(\cos{\theta_1}-\beta\sin^2{\theta_1}))\\ \Leftrightarrow\gamma^2\beta^2E_1&=\gamma^2 vp_1( \cos{\theta_1}- (1-\beta\cos{\theta_1})(\cos{\theta_1}-\beta\sin^2{\theta_1}))\\ \Leftrightarrow \beta^2E_1&\approx vp_1( \cos{\theta_1}-(1-\beta\cos{\theta_1})(\cos{\theta_1}-\beta\sin^2{\theta_1}))\\ \Leftrightarrow \beta^2E_1&\approx vp_1(\beta\cos^2{\theta_1}+\beta\sin^2{\theta_1})\\ \Leftrightarrow \beta^2E_1&\approx \beta^2E_1\\ \end{aligned}$$

这成立了！尽管我们忽略了二阶的小量，这是因为在上面的动量和角度的变换中存在的二阶误差。这说明以上谬误的源头的确是动量和夹角未进行变换。

那现在我们知道了费米的公式的问题在哪里——在反变换的时候，应该使用$\theta_1^$而不是$\theta_1$。那么问题来了，这和我$\theta_2$有什么关系呢？注意，我们在推导的时候同样误用了$\theta_2$和$\theta_2^$，这意味着在推导

$$\epsilon=\frac{\beta(\cos{\theta_2}-\cos{\theta_1})-\beta^2(\cos{\theta_2}\cos{\theta_1}-1)}{1-\beta^2}$$

的时候，我们需要替换$\theta_2$为$\theta_2^*$，即

$$\epsilon=\frac{\beta(\cos{\theta_2^*}-\cos{\theta_1})-\beta^2(\cos{\theta_2^*}\cos{\theta_1}-1)}{1-\beta^2}$$

那么正确的表达式是：

$$\begin{aligned} \epsilon&=\frac{\beta(\cos{\theta_2^*}-\cos{\theta_1})-\beta^2(\cos{\theta_2^*}\cos{\theta_1}-1)}{1-\beta^2}\\ &=\frac{\beta(\cos{\theta_2}-\beta\sin^2{\theta_2}-\cos{\theta_1})-\beta^2((\cos{\theta_2}-\beta\sin^2{\theta_2})\cos{\theta_1}-1)}{1-\beta^2}\\ &\approx\frac{\beta(\cos{\theta_2}-\cos{\theta_1})-\beta^2(\cos{\theta_2}\cos{\theta_1}-1+\sin^2{\theta_2})}{1-\beta^2}\\ &=\frac{\beta(\cos{\theta_2}-\cos{\theta_1})(1+\beta \cos{\theta_2})}{1-\beta^2}\\ \end{aligned}$$

在这个公式下计算平均能量增加率：

$$\langle\cos{\theta_1}\rangle=\frac{\int_{0}^{\pi}\cos{\theta}(v_1\cos{\theta}+v)\sin{\theta} d\theta}{\int_{0}^{\pi} (v_1\cos{\theta}+v)\sin{\theta}d\theta} \approx{-\frac13 \beta}$$ $$\langle\cos{\theta_2}\rangle=\frac{\int_{0}^{\pi}\cos{\theta}|\cos{\theta}\sin{\theta} |d\theta}{\int_{0}^{\pi} |\cos{\theta}\sin{\theta}|d\theta} =0$$ $$\langle\sin^2{\theta_2}\rangle=\frac{\int_{0}^{\pi}\sin^2{\theta}|\cos{\theta}\sin{\theta} |d\theta}{\int_{0}^{\pi} |\cos{\theta}\sin{\theta}|d\theta} =\frac12$$

所以，平均能量增加率为：

$$\langle\epsilon\rangle= \frac56\beta^2$$

无穷小速度场与平均速度场

为了解决对云团划分精度导致能量增加率不收敛的谬误，这里引入速度场以取代云团的概念。考虑某点处具有速度场$\vec{\beta}$，粒子的入射角度$\theta_1$，出射角度$\theta_2$，在极短的距离内两者是不独立的，那么：

$$\theta_2=\theta_1+d\theta$$

只保留一阶项，能量增加率为：

$$\begin{aligned} \epsilon &=\frac{\beta(\cos{\theta_2}-\cos{\theta_1})(1+\beta \cos{\theta_2})}{1-\beta^2}\\ &\approx-\beta \sin{\theta_1}d\theta\\ \end{aligned}$$

这一式子阐明了谬误的根源，即不能无限细分云团，因为会使得角度不独立。但是对于过小的云团（高精度速度场），模拟会变得十分困难，所以需要引入平均速度场的概念：在一定的方差内，将一定的区域内的速度场平均化。这样即解决了精度问题，同时解决了角度不独立的问题（使得我们可以基于费米模型模拟）。

接下来，我们需要证明，平均后的速度场和初始的速度场的效果是一样的。

对于初始的速度场，能量的增加为：

$$\begin{aligned} 1+\epsilon &=\prod_{i=1}^{n}(1+\epsilon_i)\\ &\approx\prod_{i=1}^{n}(1-\beta \sin{\theta_{i}}d\theta_i)\\ &\approx1-\sum_{i=1}^n\beta \sin{\theta_{i}}d\theta_i\\ &\approx1-\int_{\theta_1}^{\theta_2}\beta \sin{\theta_{i}}d\theta_i\\ &=1+\beta(\cos{\theta_2}-\cos{\theta_1}) \end{aligned}$$

考虑到$d\theta_i$的正负性，忽略掉二阶项是合理的。

平均后的速度场结果为：

$$\begin{aligned} 1+\epsilon &=1+\frac{\beta(\cos{\theta_2}-\cos{\theta_1})(1+\beta \cos{\theta_2})}{1-\beta^2}\\ &\approx 1+\beta(\cos{\theta_2}-\cos{\theta_1})\\ \end{aligned}$$

最终的结果是相同的。当然这只是最简单的情况，我们还需要考虑速度场的波动：

$$\begin{aligned} 1+\epsilon &\approx1-\int_{\theta_1}^{\theta_2}\beta(\theta_i) \sin{\theta_{i}}d\theta_i\\ &=1-\int_{\theta_1}^{\theta_2}\beta \sin{\theta_{i}}d\theta_i-\int_{\theta_1}^{\theta_2}\delta\beta(\theta_i) \sin{\theta_{i}}d\theta_i\\ &=1+\beta(\cos{\theta_2}-\cos{\theta_1})-\int_{\theta_1}^{\theta_2}\delta\beta(\theta_i) \sin{\theta_{i}}d\theta_i \end{aligned}$$

考虑到速度场的波动性，后一项为0。至此，我们可以说服自己，对速度场的平均化不会影响模拟的结果。

这里似乎还需要考虑速度场的方向波动，但是从$
\epsilon\approx-\beta \sin{\theta_1}d\theta$可以看到，$\sin{\theta_1}$的波动其实可以转化为$\beta$的波动，这就化归到上面的论述了。

扩散模型

假使我们用随机游走过程去阐释电子的运动，那么由于每一步是独立同分布，其方差为：

$$D(\vec{r})=(c\Delta t)^2=(\Delta L)^2$$

我们先用$\Delta L=const$ 作为近似计算。

对于一定的时间，假设粒子进行了n次随机游走，那么粒子群的分布方差为：

$$D(\vec{r})=n(\Delta L)^2$$

从模拟结果可以看出的确有一定的正态分布概率。

按理来说，这个模型不能解释spectral index不均匀的现象，因为粒子均匀分布，都是相同的能量增加率。我们试图猜想不均匀的原因：或许是外部的湍流程度比较小，导致加速效果差？所以spectral index更低？