玻尔兹曼统计
热力学量的统计表达
配分函数
热力学宏观量
粒子数
内能
广义作用力
热量和熵
自由能
能均分定理
对理想气体的应用与讨论
理想气体的热力学量
理想气体物态方程
理想气体的内能
理想气体的熵
理想气体的化学势
麦克斯韦速度分布
压强公式
双原子气体的内能和热容
平动能
振动能
转动能
经典和量子对比
固体热容的爱因斯坦理论
顺磁性固体
对于量子系统,满足定域条件(可分辨)或经典极限条件($e^{\alpha}\gg1,\frac{a_l}{\omega_l}\ll 1$)时,可以用玻尔兹曼统计处理。
热力学量的统计表达配分函数对于一个系统,其单原子配分函数定义为(这里的下标1表示单原子):
Z_1=\sum_{l}\omega_le^{-\beta \epsilon_l}我们将在 系综理论 中看到,单原子配分函数其实和正则系综的系统配分函数有着密切的联系,正是因为三大统计分布研究的是几乎无相互作用的体系,我们才能从单原子配分函数开始研究。
热力学宏观量粒子数粒子数的统计表达为:
N=\sum_{l}a_l=\sum_{l}\omega_l e^{-\alpha- ...
近独立粒子的最概然分布
统计力学简史
系统微观运动状态的描述
自由粒子的态密度
系统统计状态的描述
分布和微观状态
玻尔兹曼系统
玻色系统
费米系统
非简并条件
三大统计分布
玻尔兹曼分布
玻色-爱因斯坦分布
费米-狄拉克分布
统计力学简史从这一节开始,我们使用统计的方法看待物理问题。一开始的时候,物理学家倾向于从微观世界导出宏观统计量(比如克劳修斯导出压强公式$P=\frac13 nm \bar{v^2}$,当然,在麦克斯韦公式修正之前,克劳修斯用的是平均速率的平方),这是基于纯力学的原理。接着,麦克斯韦从概率的角度推导出了气体分子速率公式。至此为止,所有的初级统计理论被称为气体分子运动学,以区分后面的统计热力学。
玻尔兹曼在麦克斯韦公式的基础上,进行了推广,得到了麦克斯韦-玻尔兹曼分布(这也是我们即将讨论的内容)。可惜的是,这一分布只适用于近独立子系(该节标题的来源)。吉布斯突破了这一限制,其系综理论后续启发了玻色研究理想光子气体,并得到了爱因斯坦的赞赏(他后续预言了玻色-爱因斯坦凝聚,这或许是玻色-爱因斯坦分布的来源)。泡利提出不相容原理后,费米和狄拉克提出了费米-狄拉克分布。
所以我们 ...
Approximation Method
Time-independet Perturbation
Non-degenerate Perturbation
First Order Theory
Second Order Theory
Degenerate Perturbation
Two-fold Degenerate
Problem
对角化
非简并微扰
简并微扰
Example
Stark Effect
Quadratic Stark Effect
Linear Stark Effect
Fine Structure
Relative Movement Correction
Spin-Orbit Coupling
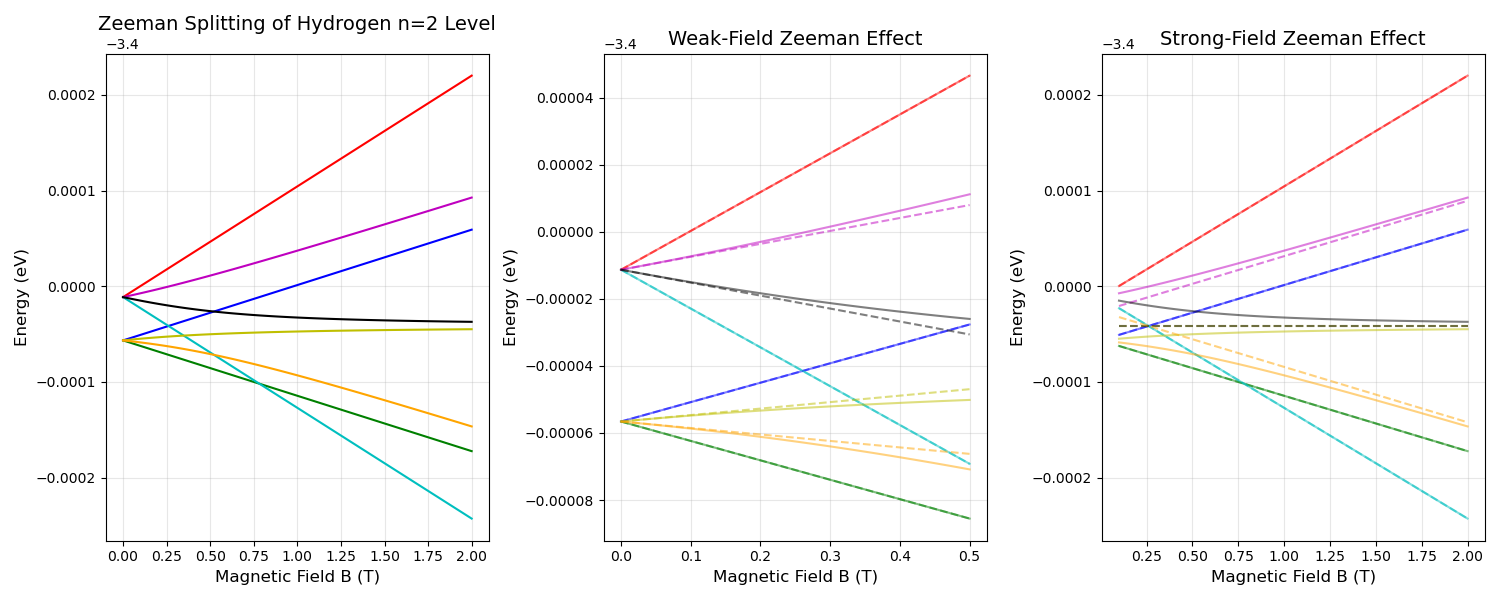
Zeeman Effect
Normal Zeeman Effect
Weak-Field Zeeman Effect
Strong-Field Zeeman Effect
Quadradic Zeeman Effect
Van der Waals Interaction
Variantional Method
Helium Atom
Hydrogen Molecular Ion
...
多元系的复相平衡和化学平衡
多元系的热力学函数和热力学方程
多元复相系的热力学函数和热力学方程
多元系的复相平衡条件
单相化学平衡条件
混合理想气体的性质
理想气体的化学平衡
均匀配比的平衡常量
电离度
热力学第三定律
多元复相系指的是拥有多种组元且至少有一个组元存在多种相的系统。在这样一个系统里面,组元之间会发生化学反应,不同相间会存在复相平衡。我们要研究的就是多元系中的复相平衡和化学平衡。
多元系的热力学函数和热力学方程广延量是一些广延量的一次齐函数,而强度量则是广延量的另次齐函数。选取多元系的$T,p,n_1,\cdots,n_k$为状态参量我们可以写出:
\begin{cases}V&=V(T,p,n_1,\cdots,n_k)\\U&=U(T,p,n_1,\cdots,n_k)\\S&=S(T,p,n_1,\cdots,n_k)\\\end{cases}由欧拉定理可知:
\begin{cases}V=\sum_i{n_i(\frac{\partial V}{\partial n_i})_{T,p,n_i}}=\sum_i{n_iv_i}\\U=\sum_i{n_i(\frac{\partial ...
Angular Momentumn and Symmetry
在经典力学中,我们通过类比动量,我们可以推广得到角动量。然而,更深层次的理解需要结合群论和对称性规律来阐释,这也是为什么起这个标题的原因。
转动和角动量对易
有限转动和无穷小转动
量子力学的无穷小转动
群论和李代数
群的基本概念
二维群
O(2) Group
SO(2) Group
U(1) Group
三维群
SO(3) Group
U(2) Group
SU(2) Group
自旋1/2系统与有限转动
基本作用力和对称性
基本作用力
对称性
对称性和简并度
对称性和守恒律
氢原子的四维旋转对称
宇称对称性
宇称算符的本征态
自发对称性破缺
宇称选择定则
时间反演对称性
经典力学的时间反演
量子力学的时间反演
时间反演算符
时间反演算符的性质
内积
算符
波函数
有自旋波函数
转动和角动量对易有限转动和无穷小转动我们在之前的学习就知道有限转动是不对易的,这意味着先进行哪个操作影响最后的结果。
我们可以写出有限转动的转动矩阵:
R_x(\phi)=\begin{pmatrix}
1&0&0\\
0&\cos{\phi}&-\sin{\phi}\\ ...
托福首考有感
写在前面
题型了解和时间安排
阅读
听力
口语
写作
综合写作
学术写作/独立写作
练习和真题使用
个人经验
硬件软件准备
单词
阅读
听力
口语
写作
考场实地
lz借助源友&小红书&b站的经验,未报班备考一个多月后还算顺利在10/27首考考出了比较满意的成绩,于此记录。
非常有用的回答和网站如下:
水源:非SJTU的同学可能需要其他校友帮助访问;
小红书-不爱酸苦辣:超级厉害的博主,口语照着她练的;
留星网:129买一个真题网站,甚至可以从真题入手练习(100套短期备考做不完);
B站-Vince9120:超级厉害的UP,其阅读听力口语写作都可以看看,尤其是写作;
B站-吴奇老师的托口秀:口语真题的简单范例,不难但是很有用;
考拉托福小程序:口语AI评分和修改;
Lingoleap:口语和写作AI评分和修改。
以下从题型了解、练习与真题使用、个人经验、考场实地来阐述。
写在前面
本人BG:四级650+,六级597,均有一定准备但是不多。如果是SJTU的同学还可以参考我的大英三四EPT72分,在交大不算很高。词汇停留在高考+六级词汇+一定的托福词汇 ...
考前必背
阅读注意最后一题不选细节。
听力放松,做笔记以提醒,当作平时听课。
口语万能理由
TimeI prefer to … , because I think … can save a lot of time in my daily life. As we all know, time is so important in these days. We can do more things and learn more skills if we can be efficient, which can be ensured by … .
MoneyI prefer to … , because I think … can save a lot of money in mydaily life. As we all know, money is so important in these days. If we can save money, we can do more things and learn more skils with the limited amount of money. ...
口语语料
Personality
主题
语料
Independence
Developing self-reliance fosters a sense of responsibility and resilience. It prepares them for more significant challenges, such as academic pursuits and social interactions.Independent children are more likely to adapt to new environments, like starting school or making new friends.
Television
PositiveTV documentaries can broaden our horizons by exposing us to different cultures and histories.Television fosters a sense of community and strengthen our soc ...
Hexo的安装与配置
建Blog有感
预备软件
Node.js
Git
注册你的Github账号
Git配置
Hexo的安装
下载Hexo
本地建站
基本命令
清理生成的静态文件
生成静态文件
启动本地服务器预览站点
部署到远程服务器
新建文章
Butterfly美化
不同电脑的同步
hexo的安装和配置教程已经很多了,但在照着安装的过程中仍然遇到了很多困难。笔者基于网络的教程进行更新和补充(顺便教教小学弟)。
建Blog有感笔者经历了从手写笔记、平板笔记一直到电脑本地用$\LaTeX$做笔记的阶段,尽管平板笔记解决了手写笔记不容易更改和整理(并且字不好看)的问题,电脑本地笔记又解决了平板笔记不方便保存和转移的问题,$\LaTeX$本身也是极为繁琐的,而Blog本身托管到Github的同时,解决了分享的问题。
阮一峰在博客中写到:
喜欢写 Blog 的人,会经历三个阶段。
第一阶段,刚接触 Blog,觉得很新鲜,试着选择一个免费空间来写。
第二阶段,发现免费空间限制太多,就自己购买域名和空间,搭建独立博客。
第三阶段,觉得独立博客的管理太麻烦,最好在保留控制权的前提下,让别人来管,自己只负 ...
对称性和守恒律
Preview
Ehrenfest定理
位力定理
对称变换
幺正变换
对称性和守恒律
对称变换与幺正变换
无穷小变换
常见的对称性和守恒律
空间平移对称和动量守恒
空间反射对称和宇称守恒
空间旋转对称和角动量守恒
时间反演对称和能量守恒
简并
矢量和标量的分类
选择定则
宇称选择定则(Laporte’s rule)
旋转选择定则(Wigner–Eckart Theorem)
绘景
薛定谔绘景
海森堡绘景
相互作用绘景
Preview在谈及对称性和守恒律之前,我们需要知道以下定理:
Ehrenfest定理\frac{d\langle A\rangle}{d t}=\left\langle\frac{\partial A}{\partial t}\right\rangle+\frac{1}{i\hbar}\langle[A,H]\rangle证明:
\begin{aligned}\frac{d\langle A\rangle}{d t}&=\frac{d }{d t}\int\psi^*\hat{A}\psi \mathrm{d}x\\&=\int\frac{\pa ...