小径

原子的负电性 晶体结合的类型 金属键 共价键 sp3杂化 离子键 范德瓦耳斯键 氢键 混合键 晶体中原子的聚集是原子间相互作用的结果，这种使原子发生聚集的强烈的相互作用就是化学键。考虑波恩近似，一个两原子体系的能量为： E=\frac{p_1^2}{2m}+\frac{p_2^2}{2m}+\frac{q_1q_2}{4\pi\epsilon_0 r}+E_{R}其中，$E_R$是电子的能量。在两原子相互靠近时，不仅会受到核间的库伦斥力，价电子的重新排布也会影响作用力$-\dfrac{\partial E(R)}{\partial R}$。价电子的重新分布情况取决于原子本身束缚电子的能力，所以，我们以下首先介绍原子本身束缚电子的能力——电负性。 原子的负电性Mulliken考虑使用原子的电离能(ionization energy)和电子亲和能(electron affinity)来定义原子的电负性： \chi=\frac{K_m}{2}(I+E_A)其中，$I$是原子的电离能，$E_A$是原子的电子亲和能。$K_m$是一个常数，通常使得Li的电负性为1.0。除此之外，还有P ...

晶格及其平移对称性 晶体结构 晶格的数学描述 初基元胞 单胞 维格纳-塞茨(Wigner-Seitz)元胞 倒点阵 晶体的宏观对称性 对称操作 对称素 平移对称性对宏观对称性的限制 对称素的组合规则 简单晶体结构的对称素 晶体点阵和结构的分类 晶体点群 点阵中的高对称点 晶体的X射线衍射 布拉格反射公式 劳厄条件 晶格及其平移对称性晶体结构几种常见的晶体结构： 简单立方晶体结构(simple cubic structure,sc) 体心立方晶体结构(body-centered cubic structure,bcc) 面心立方晶体结构(face-centered cubic structure,fcc) 六角密堆积晶体结构(hexagonal close-packed structure,hcp) 金刚石结构(diamond structure) NaCl结构 CsCl结构 闪锌矿结构 钙钛矿结构 晶体结构 原子数 配位数 原子堆积率 常见例子 sc 1 6 0.52 极少 bcc 2 8 0.68 碱金属 ...

本专题参照Kittle的《固体物理学导论》和胡安的《固体物理学》。 固体物理Content 晶体结构及其平移对称性 晶体的结合 晶格动力学 金属电子论 能带论 Bloch电子动力学 研究固体的物理学性质，首先得从其几何学性质出发，这是我们研究 晶体结构及其平移对称性 的原因。晶体学可以作为一门专门的学科，结合群论来研究。 从经典图像可以得到 晶体的结合 。 我们知道固体的量子力学描述实质上是一个多体问题。假设有N个离子实和NZ个电子，系统的哈密顿量可以写成： H=\underbrace{\sum_i\frac{\vec{p_i}^2}{2m_e}}_{\text{电子动能}}+\underbrace{\sum_n\frac{\vec{p_n}^2}{2M_n}}_{\text{离子实动能}}+\underbrace{\frac12\sum_{i\neq j}\frac{e^2}{|\vec{r_i}-\vec{r_j}|}}_{\text{电子电子相互作用}}+\underbrace{\frac12\sum_{n\neq m}\frac{Z_nZ_m e^2}{|\vec{R_n} ...

本专栏主要参考Philips的《细胞的生物物理学》。坦诚地说，我不认为这本书的架构对于物理专业的学生是友善的，因为这本书将各个模型打散，进而适应不同阶段的物理水平看上去很散乱。在这个专栏里面，我尽量将上课讲到的模型进行了统一的整理（事实上我们的老师也是这么做的）。 生物物理的主要内容为利用物理知识（尤其是热统的知识）来构建模型，进而解释生物现象。次要知识为生物的实验方法和概念。本专栏聚焦于模型的构建。 生命系统的空间和时间尺度 基础的数理化知识 平衡态模型 动力学模型 生物网络

一些重要的生物尺度

将非相对论性量子力学（NRQM）推广到相对论情形的尝试注定会是失败的，因为量子力学要求的概率守恒在相对论中不再成立，能量会产生新的粒子，因此量子场论（QFT）才是正确的框架。不过，当粒子的能量较小的时候，我们可以认为没有新粒子的产生，进而构建相对论性量子力学（RQM），Klein-Gordon方程和Dirac方程就是那时沿此思路所得的两个产物。 Klein-Gordon方程具有一些神奇的困难，不过Dirac方程却是一个很好的过渡，其以很自然的方式： 导出电子的朗德因子 导出了氢原子光谱精细结构 预言了带正电荷的反粒子——正电子的存在 Dirac方程仍然存在负能解的问题，这就是狄拉克之海的由来。 在此之前，我们先介绍有用的单位制。 自然单位制\hbar=c=1 $c=1$意味着时间和空间的单位是一样的。同时，质能方程$E=mc^2$变为$E=m$，意味着质量和能量的单位也是一样的。 $\hbar=1$意味着长度的量纲是动量的倒数，同时也是能量单位的倒数。 克莱因-戈登方程相对论中，粒子的能量为： E=\frac{p^2}{2m}\Rightarrow E=\sqrt{p^2+m^2 ...

Classic Scattering Theory Differential Cross Section Rigid Sphere Scattering Rutherford Scattering Quamtum Scattering Theory Scattering Amplitude Green Function Method Operator Form Optical Theorem Example: Square Well Example: Yukawa Potential Classic Scattering TheoryDifferential Cross Section 微分散射截面定义为： D(\theta)=\frac{d\sigma}{d\Omega}其中$d\sigma$是单位立体角$d\Omega$内的散射截面。显然，微分散射截面是一个碰撞参数$b$或角度$\theta$的函数。其中： d\sigma =4\pi bdb,d\Omega=4\pi \sin\theta d\theta所以： D(\theta)=\frac{d\sigma}{d\Om ...

量子力学2主要参考课程讲义以及Sarkari的《现代量子力学》。 Content: Basic Concept Density-Matrix Quantum Dynamics & Quantum Geometry Angular Momentumn and Symmetry Approximation Method Time-Dependent-Perturbation WKB-Approximation Scattering-Theory Relativistic-QM EPR-Paradox

相空间和刘维尔定理 系综理论 微正则系综 等概率原理 微正则系综的热力学公式 单原子经典理想气体 爱因斯坦的固体热容理论 正则系综 正则系综的热力学公式 正则系综的便利性 正则系综和微正则系综的联系 实际气体 德拜的固体热容理论 巨正则系综 吸附现象 点吸附（0维吸附） 面吸附（2维吸附） 表格 相空间和刘维尔定理最概然分布的方法处理近独立的粒子，但是不能处理有强相互作用的粒子，这时候就要请出平衡态统计物理的普遍理论——系综理论。 在经典力学中，N个全同粒子（每个粒子的自由度为r）的总自由度为$f=Nr$。那么可以通过广义坐标$q_i,i=1,\cdots,f$和广义动量$p_i,i=1,\cdots,f$构成2f维度的相空间。系统的运动状态由哈密顿正砸方程决定，即 \frac{dq_i}{dt}=\frac{\partial H}{\partial p_i},\frac{dp_i}{dt}=-\frac{\partial H}{\partial q_i}对于保守系统，哈密顿量就是系统的能量，即 H(q_1,\cdots,q_f,p_1,\cdots,p_f)=E这 ...

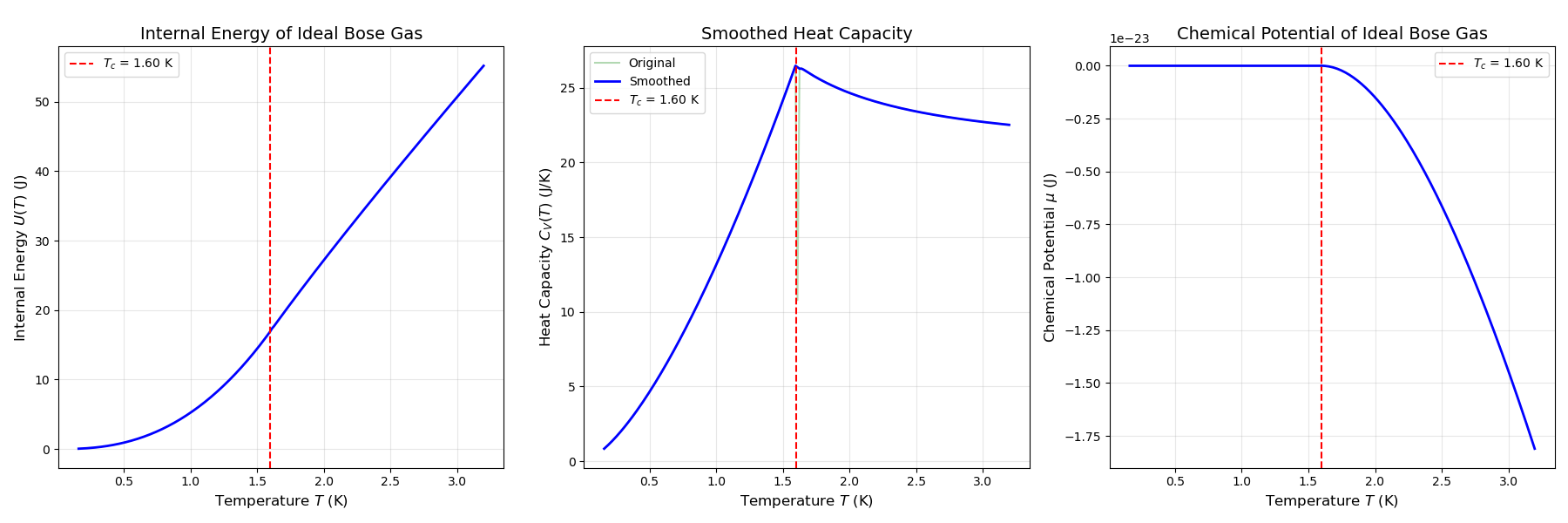
热力学统计量表达式 弱简并理想玻色气体和费米气体 玻色-爱因斯坦凝聚(BEC) 热辐射和光子气体 瑞利-金斯公式 维恩公式 普朗克公式 金属中的自由电子气体 满足定域或非简并条件的粒子系统可以采用玻尔兹曼统计，而不满足非简并条件的系统，需要用玻色-爱因斯坦统计或费米-狄拉克统计处理。 不满足非简并条件的气体叫做简并气体。不同于理想气体，简并气体不满足定域条件。尽管气体之间的距离更大，但是气体粒子本身的波包尺度也更大。同样的道理，固体虽然原子之间间距小，但是波包更小，是定域系统。 粒子的简并情况也有所区别，具体可根据逸度$z=e^{-\alpha}$进行分类： 理想气体（非简并） 理想玻色/费米气体（弱简并） 玻色-爱因斯坦凝聚 光子气体 自由电子气（强简并） $e^{-\alpha}\ll1$ $e^{-\alpha}\ll1$但不可忽略 $e^{-\alpha}\to 1^{-}$ $e^{-\alpha}= 1$ $e^{-\alpha}\gg 1$ 其中，理想气体因为忽略相互作用，所以化学势$\mu$接近0，但我们在下面会讨论如果不忽略其影响会 ...